后缀自动机详解
前言
第\(3\)次尝试学习后缀自动机……下定决心不再背板子
参考资料:
2012年noi冬令营clj讲稿
前置知识:Trie树
简介
后缀自动机,顾名思义是能识别所有后缀的自动机。那么就要从两个方面入手:什么是自动机,以及怎样让自动机识别所有后缀。
其实识别所有后缀用Trie树就可以做到,把所有后缀插到Trie里即可。但是当点数比较多的时候,Trie树\(O(n^2)\)的时间和空间复杂度就吃不消了。于是就需要后缀自动机。
自动机
有限状态自动机能识别字符串。自动机由\(5\)个部分组成,分别是字符集\(Alpha\),状态集合\(State\),初始状态\(Init\),结束状态集合\(End\),和状态转移函数\(Trans\)。如果一个自动机\(A\)能识别字符串\(S\),那么记\(A(S)=1(true)\),否则\(A(S)=0(false)\)。
定义\(Trans(R\in \{State\cup \{NULL\}\},ch/str)\)为状态\(R\)后加字符\(ch\)或字符串\(str\)所达到的状态。如果不存在则记为\(NULL\)。
容易发现自动机\(A\)能识别的串就是所有的\(S\)使得\(Trans(Init,S)\in End\)。记\(Reg(A)=\{S:Trans(Init,S)\in End\}\)。
后缀自动机概念
由上面自动机的概念,我们可以知道,一个\(String\)的SAM(suffix automaton),\(S\in Reg(SAM)\)当且仅当\(S\)是\(String\)的后缀。然而似乎Trie仍然可以满足……我们需要压缩Trie的状态!
下面不妨令\(String="aabab"\)。\(n\)为\(Length(String)\)。
我们定义\(String\)的子串\(S\)出现位置的右端点集合为\(EndPos(S)\)。例如例子中\(EndPos("ab")=\{3,5\}\)。那么,关于\(EndPos\)我们有如下几个结论:
- 如果两个串的\(EndPos\)相同,那么其中一个一定是另一个的后缀。
- 对于任意两个串\(S_1,S_2\),\(Length(S_1)\leqslant Length(S_2)\),那么\(EndPos(S_2)\subseteq EndPos(S_1)\)或\(EndPos(S_1)\cap EndPos(S_2)=\emptyset\)。
- 对于所有\(EndPos(S)\)相等的\(S\),记这些\(S\)中长度最大的长度为\(MaxLen\),长度最小的为\(MinLen\),那么对于\(\forall i(MinLen \leqslant i\leqslant MaxLen), \exists S'(EndPos(S')=EndPos(S), Length(S')=i)\)。
- 不同的\(EndPos\)最多有\(O(n)\)类。
前\(3\)点还是容易想象的,下面是对于第\(4\)点的证明:
不难发现\(\forall S, EndPos(S)\subseteq EndPos("")\)。对于某个特定的\(EndPos\)集合\(X\),取最长的\(S\)使得\(EndPos(S)=X\)。在\(X\)前面加两个不同的字符\(x,y\),那么\(EndPos(xS)\cap EndPos(yS)=\emptyset\)。而实际上还有
\[\left|\bigcup_{x\in Alpha}EndPos(xS)=EndPos(S)\right| \]所以我们可以将这看成一个划分,划分关系构成一棵树,叫做Parent树。其中,一个节点的父亲的\(MaxLen\)是这个节点的\(MinLen-1\)。这棵树最多有\(2n-1\)个节点,即不同的\(EndPos\)的个数是\(O(n)\)的。
可以看图理解一下(图中黑色部分,黄色为满足某个特定的\(EndPos\)的最长\(S\)):
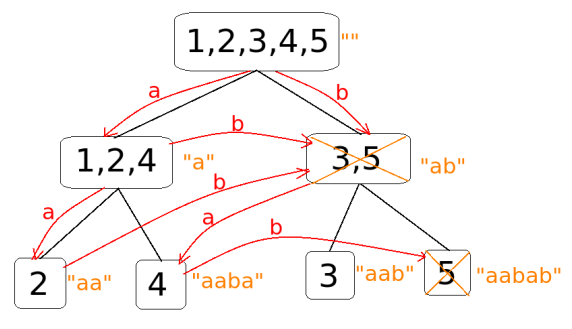
如果将这个数构建成一个完整的自动机,我们还需要定义:
- \(Init\):根节点;
- \(End\):图中带橙色叉的节点;
- \(Trans\):图中红色的边;
同时我们还可以说SAM的边数是\(O(n)\)的。坑,待填
如何构建后缀自动机
先放两张图:
如果我们已经构建好了\("aaba"\)的SAM:
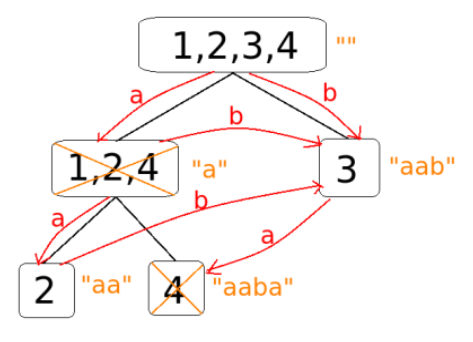
我们要构建\("aabab"\)的SAM:

上面这张图有点错误,从\(\{2\}\)指向\(\{3,5\}\)的边应该指向\(\{3\}\),从\(\{3\}\)应该有指向\(\{4\}\)的值为\(a\)的边。这点会在下面的构造过程中讲到。
我们发现,只需要更改\(EndPos\)中包含最后一个位置的点就可以了。如果我们记录了\(Last\),那需要处理的节点就是\(Last\)的祖先。不妨从叶子向根记做\(v_1,v_2,\dots\)。由于从叶子向根,\(|EndPos|\)是不断增大的。所以我们可以找到第一个\(Trans(v_i,x)\)不为空的点。将\(Trans(v_t,x)\)为空的指向新点\(newPoint\)即可,而对于另一些我们需要分类讨论。不妨记\(q=Trans(v_t,x)\)。如果强行加入\(x\),那么会使\(q\)的\(MaxLen\)变小(当然,如果不会,那么构造就结束了)。加入\(x\)后,实际上\(q\)被分为了两个部分:

所以建一个新的点\(newq\)解决这个问题。\(newq\)继承了\(q\)除了\(MaxLen\)之外的所有信息。
同时,我们还要将原图中原来指向\(q\)的点指向\(nq\)。这样就结束了!
#include <bits/stdc++.h>
using namespace std;
const int Maxn = 1000010;
struct suffixAutomaton {
int Link[ Maxn << 1 ], Len[ Maxn << 1 ], Child[ Maxn << 1 ][ 26 ];
int Last, Used;
inline void Init() {
memset( Link, 0, sizeof( Link ) );
memset( Len, 0, sizeof( Len ) );
memset( Child, 0, sizeof( Child ) );
Last = 1; Used = 1;
return;
}
void Build( int Ch ) {
int Now = ++Used, p;
Len[ Now ] = Len[ Last ] + 1;
for( p = Last; p && Child[ p ][ Ch ] == 0; p = Link[ p ] ) Child[ p ][ Ch ] = Now;
Last = Now;
if( !p ) { Link[ Now ] = 1; return; }
int q = Child[ p ][ Ch ];
if( Len[ p ] + 1 == Len[ q ] ) { Link[ Now ] = q; return; }
int Clone = ++Used;
Len[ Clone ] = Len[ p ] + 1; Link[ Clone ] = Link[ q ];
for( int i = 0; i < 26; ++i ) Child[ Clone ][ i ] = Child[ q ][ i ];
for( ; p && Child[ p ][ Ch ] == q; p = Link[ p ] ) Child[ p ][ Ch ] = Clone;
Link[ q ] = Link[ Now ] = Clone;
return;
}
};
suffixAutomaton SuffixAutomaton;
char Ch[ Maxn ];
int Len;
int main() {
scanf( "%s", Ch );
Len = strlen( Ch );
SuffixAutomaton.Init();
for( int i = 0; i < Len; ++i )
SuffixAutomaton.Build( Ch[ i ] - 'a' );
return 0;
}
练习题
#include <bits/stdc++.h>
using namespace std;
const int Maxn = 1000010;
int Ref[ Maxn ], Arr[ Maxn << 1 ];
struct suffixAutomaton {
int Link[ Maxn << 1 ], Len[ Maxn << 1 ], Child[ Maxn << 1 ][ 26 ];
int Last, Used;
//extra
int Size[ Maxn << 1 ];
inline void Init() {
memset( Link, 0, sizeof( Link ) );
memset( Len, 0, sizeof( Len ) );
memset( Child, 0, sizeof( Child ) );
Last = 1; Used = 1;
return;
}
void Build( int Ch ) {
int Now = ++Used, p;
Len[ Now ] = Len[ Last ] + 1;
Size[ Now ] = 1;//不是copy的点才能做算大小
for( p = Last; p && Child[ p ][ Ch ] == 0; p = Link[ p ] ) Child[ p ][ Ch ] = Now;
Last = Now;
if( !p ) { Link[ Now ] = 1; return; }
int q = Child[ p ][ Ch ];
if( Len[ p ] + 1 == Len[ q ] ) { Link[ Now ] = q; return; }
int Clone = ++Used;
Len[ Clone ] = Len[ p ] + 1; Link[ Clone ] = Link[ q ];
for( int i = 0; i < 26; ++i ) Child[ Clone ][ i ] = Child[ q ][ i ];
for( ; p && Child[ p ][ Ch ] == q; p = Link[ p ] ) Child[ p ][ Ch ] = Clone;
Link[ q ] = Link[ Now ] = Clone;
return;
}
inline void CollectSize( int MaxLen ) {//按照DAG的逆序求大小
memset( Ref, 0, sizeof( Ref ) );
memset( Arr, 0, sizeof( Arr ) );
for( int i = 1; i <= Used; ++i ) ++Ref[ Len[ i ] ];
for( int i = 1; i <= MaxLen; ++i ) Ref[ i ] += Ref[ i - 1 ];
for( int i = 1; i <= Used; ++i ) Arr[ Ref[ Len[ i ] ]-- ] = i;
for( int i = Used; i >= 1; --i ) Size[ Link[ Arr[ i ] ] ] += Size[ Arr[ i ] ];
return;
}
};
suffixAutomaton SuffixAutomaton;
char Ch[ Maxn ];
int Len;
int main() {
scanf( "%s", Ch );
Len = strlen( Ch );
SuffixAutomaton.Init();
for( int i = 0; i < Len; ++i ) SuffixAutomaton.Build( Ch[ i ] - 'a' );
SuffixAutomaton.CollectSize( Len );
int Ans = 0;
for( int i = 1; i <= SuffixAutomaton.Used; ++i )
if( SuffixAutomaton.Size[ i ] > 1 )
Ans = max( Ans, SuffixAutomaton.Len[ i ] * SuffixAutomaton.Size[ i ] );
printf( "%d\n", Ans );
return 0;
}
#include <bits/stdc++.h>
using namespace std;
const int Maxn = 100010;
int Ref[ Maxn ], Arr[ Maxn << 1 ];
struct suffixAutomaton {
int Link[ Maxn << 1 ], Len[ Maxn << 1 ], Child[ Maxn << 1 ][ 26 ];
int Last, Used;
//extra
int Size[ Maxn << 1 ];
inline void Init() {
memset( Link, 0, sizeof( Link ) );
memset( Len, 0, sizeof( Len ) );
memset( Child, 0, sizeof( Child ) );
memset( Size, 0, sizeof( Size ) );
Last = 1; Used = 1;
return;
}
void Build( int Ch ) {
int Now = ++Used, p;
Len[ Now ] = Len[ Last ] + 1;
Size[ Now ] = 1;//不是copy的点才能做算大小
for( p = Last; p && Child[ p ][ Ch ] == 0; p = Link[ p ] ) Child[ p ][ Ch ] = Now;
Last = Now;
if( !p ) { Link[ Now ] = 1; return; }
int q = Child[ p ][ Ch ];
if( Len[ p ] + 1 == Len[ q ] ) { Link[ Now ] = q; return; }
int Clone = ++Used;
Len[ Clone ] = Len[ p ] + 1; Link[ Clone ] = Link[ q ];
for( int i = 0; i < 26; ++i ) Child[ Clone ][ i ] = Child[ q ][ i ];
for( ; p && Child[ p ][ Ch ] == q; p = Link[ p ] ) Child[ p ][ Ch ] = Clone;
Link[ q ] = Link[ Now ] = Clone;
return;
}
inline void CollectSize( int MaxLen ) {//按照DAG的逆序求大小
memset( Ref, 0, sizeof( Ref ) );
memset( Arr, 0, sizeof( Arr ) );
for( int i = 1; i <= Used; ++i ) ++Ref[ Len[ i ] ];
for( int i = 1; i <= MaxLen; ++i ) Ref[ i ] += Ref[ i - 1 ];
for( int i = 1; i <= Used; ++i ) Arr[ Ref[ Len[ i ] ]-- ] = i;
for( int i = Used; i >= 1; --i ) Size[ Link[ Arr[ i ] ] ] += Size[ Arr[ i ] ];
return;
}
};
suffixAutomaton SuffixAutomaton;
char Ch[ Maxn ];
int Len;
int Count[ Maxn ];
void Work() {
scanf( "%s", Ch );
Len = strlen( Ch );
SuffixAutomaton.Init();
for( int i = 0; i < Len; ++i ) SuffixAutomaton.Build( Ch[ i ] - 'a' );
SuffixAutomaton.CollectSize( Len );
int k; scanf( "%d", &k );
int Max = 1, Ans = -1;
memset( Count, 0, sizeof( Count ) );
for( int i = 1; i <= SuffixAutomaton.Used; ++i )
if( SuffixAutomaton.Size[ i ] == k ) {
--Count[ SuffixAutomaton.Len[ i ] + 1 ];
++Count[ SuffixAutomaton.Len[ SuffixAutomaton.Link[ i ] ] + 1 ];
}
for( int i = 1; i <= Len; ++i ) Count[ i ] += Count[ i - 1 ];
for( int i = 0; i <= Len; ++i )
if( Count[ i ] >= Max ) {
Max = Count[ i ];
Ans = i;
}
printf( "%d\n", Ans );
return;
}
int main() {
int TestCases; scanf( "%d", &TestCases );
for( ; TestCases--; ) Work();
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号