[oiclass2865]小奇的仓库:树形DP+换根
题目
小奇采的矿实在太多了,它准备在喵星系建个矿石仓库。令它无语的是,喵星系的货运飞船引擎还停留在上元时代!
喵星系有\(n\)个星球,星球以及星球间的航线形成一棵树。
从星球\(a\)到星球\(b\)要花费 \([dis(a,b)\ Xor\ M]\)秒。(\(dis(a,b)\)表示\(ab\)间的航线长度,\(Xor\) 为位运算中的异或)
为了给仓库选址,小奇想知道,星球 \(i(1<=i<=n)\) 到其它所有星球花费的时间之和。
输入
第一行包含两个正整数 \(n,M\)。
接下来 \(n-1\) 行,每行 \(3\) 个正整数 \(a,b,c\),表示 \(a,b\) 之间的航线长度为 \(c\)。
输出
\(n\) 行,每行一个整数,表示星球i到其它所有星球花费的时间之和。
输入样例
4 0
1 2 1
1 3 2
1 4 3
输出样例
6
8
10
12
数据范围
|
测试点编号 |
$N$ |
$M$ |
|
1 |
$6$ |
$0$ |
|
2 |
$100$ |
$5$ |
|
3 |
$2000$ |
$9$ |
|
4 |
$50000$ |
$0$ |
|
5 |
$50000$ |
$0$ |
|
6 |
$50000$ |
$1$ |
|
7 |
$50000$ |
$6$ |
|
8 |
$100000$ |
$10$ |
|
9 |
$100000$ |
$13$ |
|
10 |
$100000$ |
$15$ |
题解
本题花了我一个上午的时间来研究,也参考了网络上不少题解,当我理解了本题的正解后,觉得网络上的题解太难懂了,有点复杂化了,所以特意写一篇能够好理解的题解。
1、如果没有异或的情况
如果没有异或的情况(即m==0的情况),就是一个简单的换根DP。设\(sum[i]\)表示从星球i到其他所有星球的花费时间之和,dep[i]表示结点i到根结点的带权路径和,size[i]表示以i为根的子树的结点个数之和。我们先dfs一遍,求出sum[1],即\(sum[1]=\sum dep[i]\)。
然后考虑换根,当从根u转移到儿子v时,\(sum[v]=sum[u]-size[v]*w+(n-size[v])*w=sum[u]+(n-2*size[v])*w\)。
代码如下:
点击查看代码
#include<bits/stdc++.h>
using namespace std;
#define int long long
const int N=100000+5;
struct edge{
int u,v,w;
};
vector<edge> g[N];
int n,m,sum[N],size[N],dep[N];
void dfs(int u,int fa){
size[u]=1;
sum[1]+=dep[u];
for(int i=0;i<g[u].size();i++){
int v=g[u][i].v;
int w=g[u][i].w;
if(v==fa)continue;
dep[v]=dep[u]+w;
dfs(v,u);
size[u]+=size[v];
}
}
void change_root(int u,int fa){
for(int i=0;i<g[u].size();i++){
int v=g[u][i].v;
int w=g[u][i].w;
if(v==fa)continue;
sum[v]=sum[u]+(n-2*size[v])*w;
change_root(v,u);
}
}
signed main(){
scanf("%lld %lld",&n,&m);
for(int i=1,u,v,w;i<n;i++){
scanf("%lld %lld %lld",&u,&v,&w);
g[u].push_back((edge){u,v,w});
g[v].push_back((edge){v,u,w});
}
dfs(1,-1);
change_root(1,-1);
for(int i=1;i<=n;i++){
printf("%lld\n",sum[i]);
}
}
2、考虑有异或的情况
我们换一种方式来求路径和
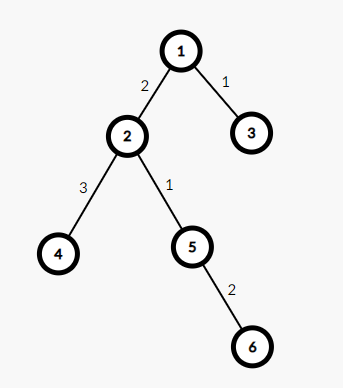
如上图,走到根的路径有5条,分别是\(2\rightarrow 1\),\(3\rightarrow 1\),\(4\rightarrow 3\rightarrow 1\),\(5\rightarrow 2\rightarrow 1\),\(6\rightarrow 5\rightarrow 2\rightarrow 1\),对应的路径和分别是\(2,1,5,3,5\)
我们设f[i][j]表示走到点i其值为j的路径个数,如上例中,\(f[1][5]=2\),即走到根节点1,其路径权值为5的方案数有2个。
根据上图我们得到\(f[1][j]\)的值:
f[1][0]=1 表示自己到自己的方案数
f[1][1]=1
f[1][2]=1
f[1][3]=1
f[1][4]=0
f[1][5]=2
有了\(f[i][j]\)数组有什么用呢?
显然,我们的答案就是\(sum[1]=\sum_{j=0}^{inf}j*f[1][j]\),即把每条路径的权值乘以路径数量再累加。
如果要异或呢?直接将权值异或就可以了,即\(sum[1]=\sum_{j=0}^{inf} (j\ Xor\ m)*f[1][j]\)
接下来考虑\(f[][]\)的转态转移。
对于\((u,v)\)这一对结点,\(u\)是父亲,\(v\)是儿子,设其边权为\(w\),则\(f[u][j+w]+=f[v][j]\),即走到\(v\)的路径和为\(j\),经过\(w\)这条边到达\(u\),则其路径和为\(j+w\),所以方案数累加。对于\(v\)结点,枚举所有的\(j\)。
但问题是,我们不知道\(j\)的范围,即我们不知道路径和最大是多少,而且,即使知道路径和最大时多少,对于每个结点都要枚举\(j\),也会超时。
现在到了本道题最费解的地方了。观察题目中的异或值\(m\),发现\(m\)的值很小,不大于\(15\)。这意味着什么呢?当两个数进行异或时,只有二进制下的末\(4\)位会受影响。这样我们可以把一个值拆成两部分来看,对于变量\(t\),\(t/16\)这一部分是不受异或值m影响的,我们可以像第1点中提到的方法正常求解。对于\(t\%16\)部分,我们采用f[i][j]统计方案的方法来进行异或处理。这样,我们枚举j时,只需要枚举\(0\sim 15\)的值即可。但事实上,我们可以不用考虑\(t/16\)部分,求出\(t\%16\),则\(t-(t\%16)+((t\%16)\ xor\ m)\)即为\(t\ xor\ m\)答案。
具体实现,我们可以dfs一遍,求出原有路径和\(sum[1]\),再统计16以内的路径方案数,具体看代码:
点击查看代码
void dfs(int u,int fa){
size[u]=1;
sum[1]+=dep[u];
f[u][0]=1;//表示自己到自己也是一种方案
for(int i=0;i<g[u].size();i++){
int v=g[u][i].v;
int w=g[u][i].w;
if(v==fa)continue;
dep[v]=dep[u]+w;
dfs(v,u);
size[u]+=size[v];
for(int j=0;j<16;j++){
f[u][(j+w)%16]+=f[v][j];
}
}
}
3、考虑换根的情况
\(sum[u]\)的换根前面已经解释了,我们看看换根时,\(f[][]\)数组如何转移。
设当前根为\(u\),儿子为\(v\),边权为\(w\)。现在要将根转移到\(v\)。
先看当根为\(u\)时,\(v\)的信息是如何叠加到\(u\)的,即\(f[u][(j+w)\%16]+=f[v][j]\),现在要转移到根\(v\)了,那么这部分叠加需要回滚回来,即\(f[u][(j+w)\%16]-f[v][j]\),然后,改成从\(u\)走向\(v\),即\(f[v][(j+w)\%16]+=f[u][j]\)。原理是这个原理,但是有细节,在转移的过程中,不能具体改变\(f[u][j]\)的值,我们可以将\(f[u][j]\)的值临时存到一个数组\(a\)中。为什么不能改变\(f[u][j]\)的值呢?因为\(u\)有多个儿子,每个根的转移都要依赖原有的\(u\)的信息。
代码如下:
点击查看代码
void change_root(int u,int fa){
for(int i=0;i<g[u].size();i++){
int v=g[u][i].v;
int w=g[u][i].w;
if(v==fa)continue;
sum[v]=sum[u]+(n-2*size[v])*w;
memset(a,0,sizeof(a));
for(int j=0;j<16;j++){
a[(j+w)%16]=f[u][(j+w)%16]-f[v][j];
}
for(int j=0;j<16;j++){
f[v][(j+w)%16]+=a[j];
}
change_root(v,u);
}
}
完整代码
点击查看代码
#include<bits/stdc++.h>
using namespace std;
#define int long long
const int N=100000+5;
struct edge{
int u,v,w;
};
vector<edge> g[N];
int n,m,sum[N],size[N],dep[N],f[N][17],a[17];
void dfs(int u,int fa){
size[u]=1;
sum[1]+=dep[u];
f[u][0]=1;//表示自己到自己也是一种方案
for(int i=0;i<g[u].size();i++){
int v=g[u][i].v;
int w=g[u][i].w;
if(v==fa)continue;
dep[v]=dep[u]+w;
dfs(v,u);
size[u]+=size[v];
for(int j=0;j<16;j++){
f[u][(j+w)%16]+=f[v][j];
}
}
}
void change_root(int u,int fa){
for(int i=0;i<g[u].size();i++){
int v=g[u][i].v;
int w=g[u][i].w;
if(v==fa)continue;
sum[v]=sum[u]+(n-2*size[v])*w;
memset(a,0,sizeof(a));
for(int j=0;j<16;j++){
a[(j+w)%16]=f[u][(j+w)%16]-f[v][j];
}
for(int j=0;j<16;j++){
f[v][(j+w)%16]+=a[j];
}
change_root(v,u);
}
}
signed main(){
scanf("%lld %lld",&n,&m);
for(int i=1,u,v,w;i<n;i++){
scanf("%lld %lld %lld",&u,&v,&w);
g[u].push_back((edge){u,v,w});
g[v].push_back((edge){v,u,w});
}
dfs(1,-1);
change_root(1,-1);
for(int i=1;i<=n;i++){
f[i][0]--;//i是根,不需统计自己到自己的方案
for(int j=0;j<16;j++){
sum[i]+=(j^m)*f[i][j]-j*f[i][j];
}
printf("%lld\n",sum[i]);
}
}


