实验四

任务一

验证性实验

源码

#include <stdio.h>
#define N 4
#define M 2

void test1() {
    int x[N] = {1, 9, 8, 4};          
    int i;

    // 输出数组x占用的内存字节数
    printf("sizeof(x) = %d\n", sizeof(x));

    // 输出每个元素的地址、值 
    for (i = 0; i < N; ++i)
        printf("%p: %d\n", &x[i], x[i]);

    // 输出数组名x对应的值 
	printf("x = %p\n", x); 
}

void test2() {
    int x[M][N] = {{1, 9, 8, 4}, {2, 0, 4, 9}};
    int i, j;

    // 输出二维数组x占用的内存字节数
    printf("sizeof(x) = %d\n", sizeof(x));

    // 输出每个元素的地址、值 
    for (i = 0; i < M; ++i)
        for (j = 0; j < N; ++j)
            printf("%p: %d\n", &x[i][j], x[i][j]);
    printf("\n");

    // 输出二维数组名x, 以及，x[0], x[1]的值
    printf("x = %p\n", x);
    printf("x[0] = %p\n", x[0]);
    printf("x[1] = %p\n", x[1]);
    printf("\n");
}

int main() {
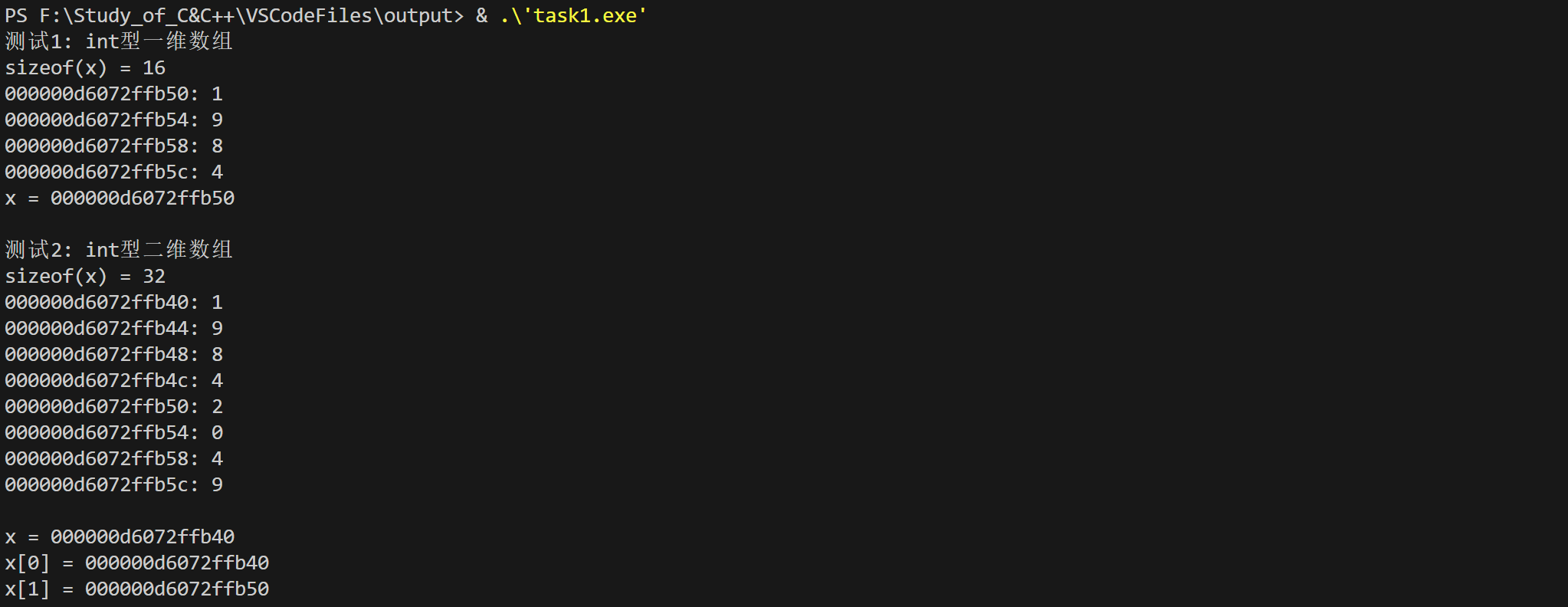
    printf("测试1: int型一维数组\n");
    test1();

    printf("\n测试2: int型二维数组\n");
    test2();

    return 0;
}

结果

回答

1. 是连续存放的，其地址与索引为0的值地址相同
2. 是不一样的，x[0]与x[1]的差值为十进制16，为两个字节，是int类型的长度

任务二

验证一维数组作为函数形参的用法

源码

#include <stdio.h>
#define N 100

// 函数声明
void input(int x[], int n);
double compute(int x[], int n);

int main() {
    int x[N];
    int n, i;
    double ans;

    while(printf("Enter n: "), scanf("%d", &n) != EOF) {
        input(x, n);            // 函数调用
        ans = compute(x, n);    // 函数调用
        printf("ans = %.2f\n\n", ans);
    }

    return 0;
}

// 函数定义
void input(int x[], int n) {
    int i;

    for(i = 0; i < n; ++i)
        scanf("%d", &x[i]);
}

// 函数定义
double compute(int x[], int n) {
    int i, high, low;
    double ans;

    high = low = x[0];
    ans = 0;

    for(i = 0; i < n; ++i) {
        ans += x[i];

        if(x[i] > high)
            high = x[i];
        else if(x[i] < low)
            low = x[i];
    }

    ans = (ans - high - low)/(n-2);

    return ans;
}

结果

回答

1. input函数作用是输出提示词并获取输入的长度为n的数组
2. compute函数作用是计算得到的数组的除极均值

任务三

验证二维数组作为函数形参的用法

源码

#include <stdio.h>
#define N 100

// 函数声明
void output(int x[][N], int n);
void init(int x[][N], int n, int value);

int main() {
    int x[N][N];
    int n, value;

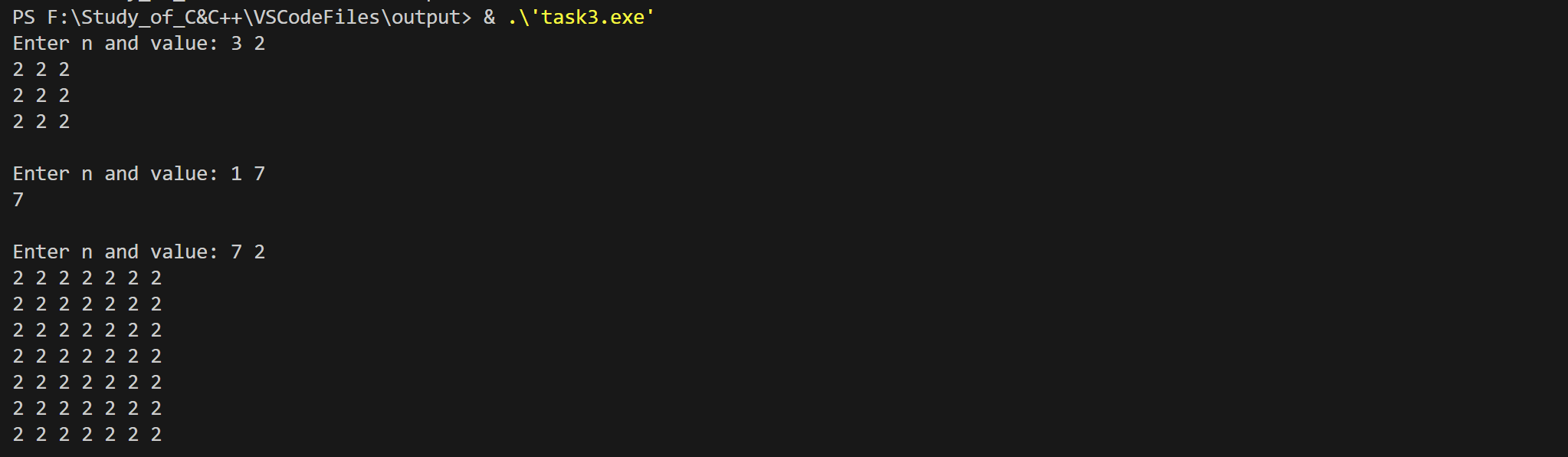
    while(printf("Enter n and value: "), scanf("%d%d", &n, &value) != EOF) {
        init(x, n, value);  // 函数调用
        output(x, n);       // 函数调用
        printf("\n");
    }

    return 0;
}

// 函数定义
void output(int x[][N], int n) {
    int i, j;

    for(i = 0; i < n; ++i) {
        for(j = 0; j < n; ++j)
            printf("%d ", x[i][j]);
        printf("\n");
    }
}

// 函数定义
void init(int x[][N], int n, int value) {
    int i, j;

    for(i = 0; i < n; ++i)
        for(j = 0; j < n; ++j)
            x[i][j] = value;
}

结果

回答

1. 二维数组参数输入时，第二维的参数不能省略
2. init函数作用是初始化一个n阶的值为value的矩阵
3. output函数作用是打印输出上面这个矩阵

任务四

计算一组数据中值

中值在统计学中定义如下：

一组数据集有序排序后，如果数据集个数是奇数，中值就是排序后位于正中间的那个数值；如果数据集个数是偶数，排序后中值就是中间两个数均值。

例如：

{1, 2, 3, 4, 5}中值是3

{1, 2, 3, 4, 5, 6}中值是(3+4)/2 = 3.5

源码

#include <stdio.h>
#define N 100

// 函数声明
void input(int x[], int n);
double median(int x[], int n);

int main()
{
    int x[N];
    int n;
    double ans;

    while (printf("Enter n: "), scanf("%d", &n) != EOF)
    {
        input(x, n);
        ans = median(x, n);
        printf("ans = %g\n\n", ans);
    }

    return 0;
}

// 函数定义
void input(int x[], int n)
{
    for (int i = 0; i < n; i++)
        scanf("%d", &x[i]);
}

double median(int x[], int n)
{
    for (int i = 0; i < n - 1; i++)
        for (int j = i + 1; j < n; j++)
            if (x[i] > x[j])
            {
                int t = x[i];
                x[i] = x[j];
                x[j] = t;
            }

    return (n % 2 == 0) ? (x[n / 2 - 1] + x[n / 2]) / 2.0 : x[n / 2];
}

结果

任务五

实现数值阵列处理

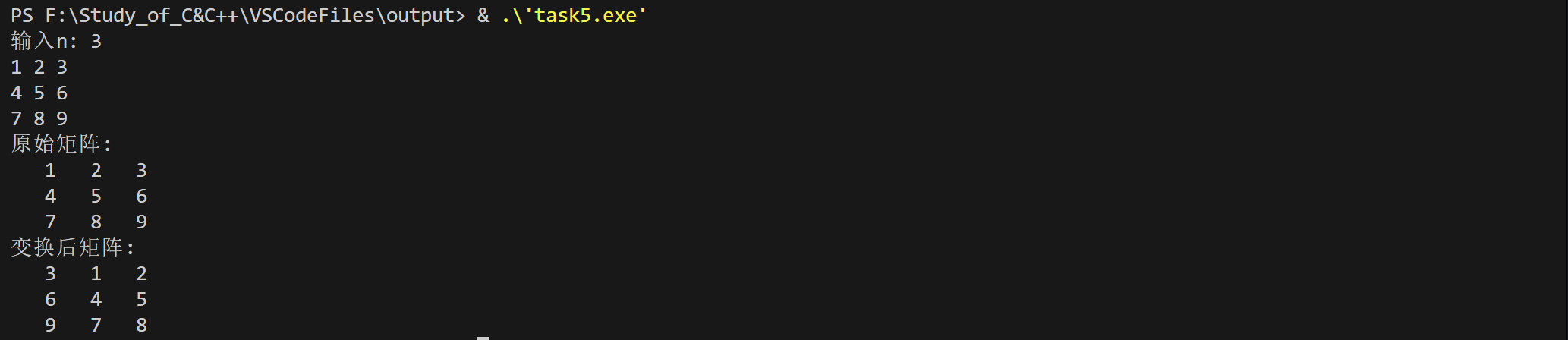
• 设计、编写函数 rotate_to_right ，实现将一个 \(n\) × \(n\) (\(n <= 100\))的方阵，按列循环右移。最右边移出去的一列数据绕回左边。

\[\begin{matrix} 1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 9 \end{matrix} \xrightarrow{\text { 按列循环右移 }} \begin{matrix} 3 & 1 & 2 \\ 6 & 4 & 5 \\ 9 & 7 & 8 \end{matrix} \]

• 在 main 中编写主体代码：输出原始方阵，调用 rotate_to_right 按列循环右移，输出变换后方阵。
  

源码

#include <stdio.h>
#define N 100

// 函数声明
void input(int x[][N], int n);
void output(int x[][N], int n);
// 函数rotate_to_right声明
void rotate_to_right(int x[][N], int n);

int main()
{
    int x[N][N];
    int n;

    printf("输入n: ");
    scanf("%d", &n);
    input(x, n);

    printf("原始矩阵:\n");
    output(x, n);

    // 函数rotate_to_right调用
    rotate_to_right(x, n);

    printf("变换后矩阵:\n");
    output(x, n);

    return 0;
}

// 函数定义
// 功能: 输入一个n*n的矩阵x
void input(int x[][N], int n)
{
    int i, j;

    for (i = 0; i < n; ++i)
    {
        for (j = 0; j < n; ++j)
            scanf("%d", &x[i][j]);
    }
}

// 函数定义
// 功能: 输出一个n*n的矩阵x
void output(int x[][N], int n)
{
    int i, j;

    for (i = 0; i < n; ++i)
    {
        for (j = 0; j < n; ++j)
            printf("%4d", x[i][j]);

        printf("\n");
    }
}

// 函数rotate_to_right定义
// 功能: 把一个n*n的矩阵x，每一列向右移, 最右边被移出去的一列绕回左边
void rotate_to_right(int x[][N], int n)
{
    for (int i = 0; i < n; i++)
    {
        int temp = x[i][n - 1];
        for (int j = n - 1; j > 0; j--)
        {
            x[i][j] = x[i][j - 1];
        }
        x[i][0] = temp;
    }
}

结果

任务六

实现进制转换

源码

#include <stdio.h>
#define N 100

void dec_to_n(int x, int n); // 函数声明

int main() {
    int x;

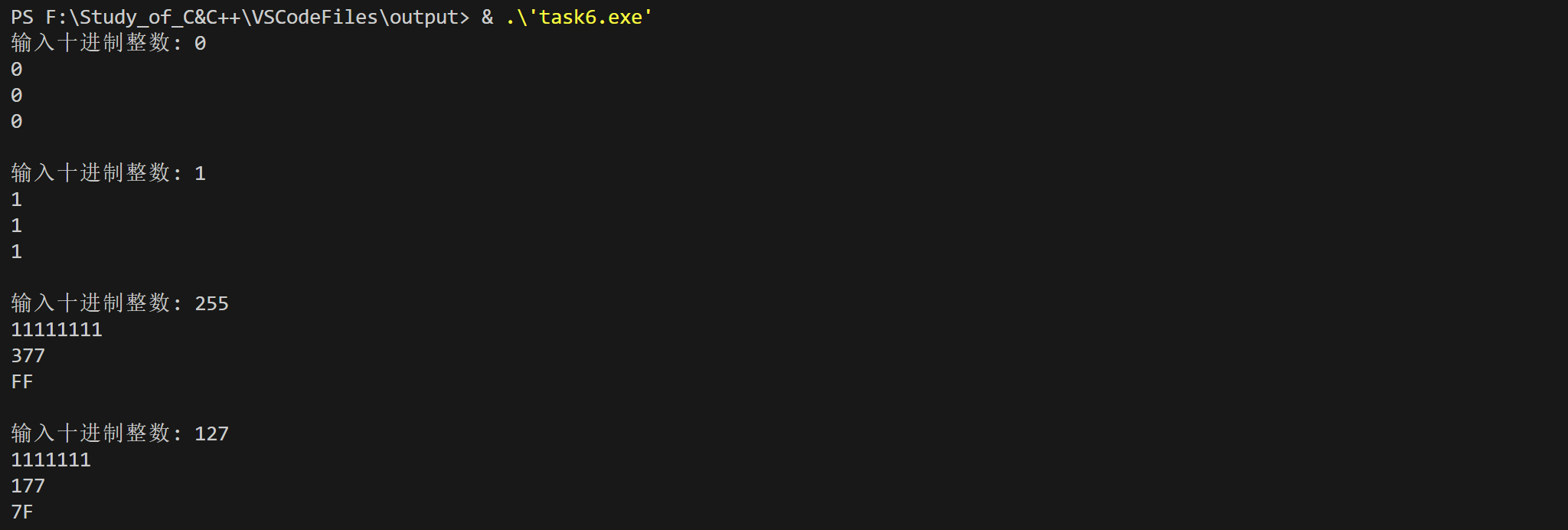
    while(printf("输入十进制整数: "), scanf("%d", &x) != EOF) {
        dec_to_n(x, 2);  // 函数调用: 把x转换成二进制输出
        dec_to_n(x, 8);  // 函数调用: 把x转换成八进制输出
        dec_to_n(x, 16); // 函数调用: 把x转换成十六进制输出

        printf("\n");
    }

    return 0;
}

// 函数定义
// 功能: 把十进制数x转换成n进制，打印输出
void dec_to_n(int x, int n) {
    char ans[N];
    int i = 0;

    do {
        int t = x % n;
        ans[i++] = (t < 10) ? (t + '0') : (t - 10 + 'A');
        x /= n;
    } while (x);

    for (int j = i - 1; j >= 0; j--) {
        printf("%c",ans[j]);
    }
    printf("\n");
}

结果

任务七

判断魔方矩阵

魔方矩阵定义如下：

魔方矩阵，是一个n×n（n为奇数）的方阵。其元素值为1, 2, 3, 4, ...，n2。

这些元素在矩阵中的位置要确保方阵每行、每列、每条对角线上的和都相等。

不就是幻方吗（）

源码

#include <stdio.h>
#define N 100

// 函数声明
void input(int x[][N], int n);
void output(int x[][N], int n);
// 待补足函数is_magic声明
int is_magic(int x[][N], int n);

int main() {
    int x[N][N];
    int n;

    while(printf("输入n: "), scanf("%d", &n) != EOF) {
        printf("输入方阵:\n");  
        input(x, n); 

        printf("输出方阵:\n");  
        output(x, n);   

        if(is_magic(x, n))
            printf("是魔方矩阵\n\n");
        else
            printf("不是魔方矩阵\n\n");
    }

    return 0;
}

// 函数定义
// 功能: 输入一个n*n的矩阵x
void input(int x[][N], int n) {
    int i, j;
    
    for (i = 0; i < n; ++i) {
        for (j = 0; j < n; ++j)
            scanf("%d", &x[i][j]);
    }
}

// 功能: 输出一个n*n的矩阵x
void output(int x[][N], int n) {
    int i, j;

    for (i = 0; i < n; ++i) {
        for (j = 0; j < n; ++j)
            printf("%4d", x[i][j]);

        printf("\n");
    }
}


// 功能: 判断一个n阶方阵是否为魔方矩阵，如果是，返回1，否则，返回0
// 待补足函数is_magic定义
int is_magic(int x[][N], int n) {
    int sum = 0, temp;

    for (int j = 0; j < n; ++j)
        sum += x[0][j];

    for (int i = 1; i < n; ++i) {
        temp = 0;
        for (int j = 0; j < n; ++j)
            temp += x[i][j];
        if (temp != sum)
            return 0;
    }

    for (int j = 0; j < n; ++j) {
        temp = 0;
        for (int i = 0; i < n; ++i)
            temp += x[i][j];
        if (temp != sum)
            return 0;
    }

    temp = 0;
    for (int i = 0; i < n; ++i)
        temp += x[i][i];
    if (temp != sum)
        return 0;

    temp = 0;
    for (int i = 0; i < n; ++i)
        temp += x[i][n - i - 1];
    if (temp != sum)
        return 0;

    return 1;
}

结果

任务八

寻找神奇的69

源码

#include <stdio.h>

void bubble_sort(int arr[], int n)
{
    for (int i = 0; i < n - 1; i++)
        for (int j = 0; j < n - i - 1; j++)
            if (arr[j] > arr[j + 1])
            {
                int t = arr[j];
                arr[j] = arr[j + 1];
                arr[j + 1] = t;
            }
}

int is_the_num(int num)
{
    int a = num * num;
    int b = num * num * num;
    int s[15], i = 0;

    while (a)
    {
        s[i] = a % 10;
        a /= 10;
        i++;
    }
    while (b)
    {
        s[i] = b % 10;
        b /= 10;
        i++;
    }
    if (i != 10)
        return 0;

    bubble_sort(s, i);

    for (int j = 0; j < 10; j++)
        if (s[j] != j)
            return 0;

    return 1;
}

int main()
{
    for (int i = 40; i <= 100; i++)
    {
        if (is_the_num(i))
        {
            printf("%d\n", i);
        }
    }
    return 0;
}

结果

$\_\_EOF\_\_$