算法工程师面试常考手撕题(一)—— AI深度学习算法
手撕 numpy写线性回归的随机梯度下降(stochastic gradient descent,SGD)
在每次更新时用1个样本,可以看到多了随机两个字,随机也就是说我们用样本中的一个例子来近似我所有的样本,来调整θ,因而随机梯度下降是会带来一定的问题,因为计算得到的并不是准确的一个梯度,对于最优化问题,凸问题,虽然不是每次迭代得到的损失函数都向着全局最优方向, 但是大的整体的方向是向全局最优解的,最终的结果往往是在全局最优解附近。
# 数据加载
from sklearn.datasets import fetch_california_housing
from sklearn.model_selection import train_test_split
X, Y = fetch_california_housing(return_X_y=True)
X.shape, Y.shape # (20640, 8), (20640, )
# 数据预处理
ones = np.ones(shape=(X.shape[0], 1))
X = np.hstack([X, ones])
validate_size = 0.2
X_train, X_test, Y_train, Y_test = train_test_split(X, Y, test_size=validate_size, shuffle=True)
# batch 函数
def get_batch(batchsize: int, X: np.ndarray, Y: np.ndarray):
assert 0 == X.shape[0]%batchsize, f'{X.shape[0]}%{batchsize} != 0'
batchnum = X.shape[0]//batchsize
X_new = X.reshape((batchnum, batchsize, X.shape[1]))
Y_new = Y.reshape((batchnum, batchsize, ))
for i in range(batchnum):
yield X_new[i, :, :], Y_new[i, :]
# 损失函数
def mse(X: np.ndarray, Y: np.ndarray, W: np.ndarray):
return 0.5 * np.mean(np.square(X@W-Y))
def diff_mse(X: np.ndarray, Y: np.ndarray, W: np.ndarray):
return X.T@(X@W-Y) / X.shape[0]
# 模型训练
lr = 0.001 # 学习率
num_epochs = 1000 # 训练周期
batch_size = 64 # |每个batch包含的样本数
validate_every = 4 # 多少个周期进行一次检验
def train(num_epochs: int, batch_size: int, validate_every: int, W0: np.ndarray, X_train: np.ndarray, Y_train: np.ndarray, X_test: np.ndarray, Y_test: np.ndarray):
loop = tqdm(range(num_epochs))
loss_train = []
loss_validate = []
W = W0
# 遍历epoch
for epoch in loop:
loss_train_epoch = 0
# 遍历batch
for x_batch, y_batch in get_batch(64, X_train, Y_train):
loss_batch = mse(X=x_batch, Y=y_batch, W=W)
loss_train_epoch += loss_batch*x_batch.shape[0]/X_train.shape[0]
grad = diff_mse(X=x_batch, Y=y_batch, W=W)
W = W - lr*grad
loss_train.append(loss_train_epoch)
loop.set_description(f'Epoch: {epoch}, loss: {loss_train_epoch}')
if 0 == epoch%validate_every:
loss_validate_epoch = mse(X=X_test, Y=Y_test, W=W)
loss_validate.append(loss_validate_epoch)
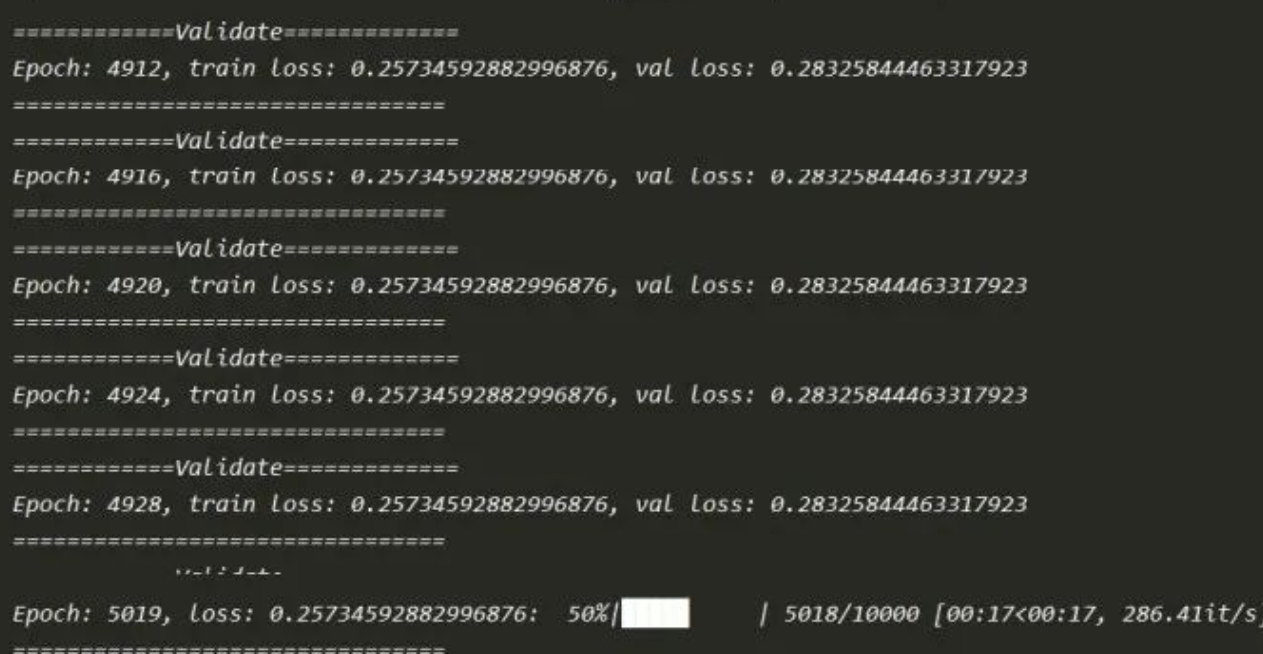
print('============Validate=============')
print(f'Epoch: {epoch}, train loss: {loss_train_epoch}, val loss: {loss_validate_epoch}')
print('================================')
plot_loss(np.array(loss_train), np.array(loss_validate), validate_every)
# 程序运行
W0 = np.random.random(size=(X.shape[1], )) # 初始权重
train(num_epochs=num_epochs, batch_size=batch_size, validate_every=validate_every, W0=W0, X_train=X_train, Y_train=Y_train, X_test=X_test, Y_test=Y_test)
手撕反向传播(backward propagation,BP)法
BP算法就是反向传播,要输入的数据经过一个前向传播会得到一个输出,但是由于权重的原因,所以其输出会和你想要的输出有差距,这个时候就需要进行反向传播,利用梯度下降,对所有的权重进行更新,这样的话在进行前向传播就会发现其输出和你想要的输出越来越接近了。
# 生成权重以及偏执项layers_dim代表每层的神经元个数,
#比如[2,3,1]代表一个三成的网络,输入为2层,中间为3层输出为1层
def init_parameters(layers_dim):
L = len(layers_dim)
parameters ={}
for i in range(1,L):
parameters["w"+str(i)] = np.random.random([layers_dim[i],layers_dim[i-1]])
parameters["b"+str(i)] = np.zeros((layers_dim[i],1))
return parameters
def sigmoid(z):
return 1.0/(1.0+np.exp(-z))
# sigmoid的导函数
def sigmoid_prime(z):
return sigmoid(z) * (1-sigmoid(z))
# 前向传播,需要用到一个输入x以及所有的权重以及偏执项,都在parameters这个字典里面存储
# 最后返回会返回一个caches里面包含的 是各层的a和z,a[layers]就是最终的输出
def forward(x,parameters):
a = []
z = []
caches = {}
a.append(x)
z.append(x)
layers = len(parameters)//2
# 前面都要用sigmoid
for i in range(1,layers):
z_temp =parameters["w"+str(i)].dot(x) + parameters["b"+str(i)]
z.append(z_temp)
a.append(sigmoid(z_temp))
# 最后一层不用sigmoid
z_temp = parameters["w"+str(layers)].dot(a[layers-1]) + parameters["b"+str(layers)]
z.append(z_temp)
a.append(z_temp)
caches["z"] = z
caches["a"] = a
return caches,a[layers]
# 反向传播,parameters里面存储的是所有的各层的权重以及偏执,caches里面存储各层的a和z
# al是经过反向传播后最后一层的输出,y代表真实值
# 返回的grades代表着误差对所有的w以及b的导数
def backward(parameters,caches,al,y):
layers = len(parameters)//2
grades = {}
m = y.shape[1]
# 假设最后一层不经历激活函数
# 就是按照上面的图片中的公式写的
grades["dz"+str(layers)] = al - y
grades["dw"+str(layers)] = grades["dz"+str(layers)].dot(caches["a"][layers-1].T) /m
grades["db"+str(layers)] = np.sum(grades["dz"+str(layers)],axis = 1,keepdims = True) /m
# 前面全部都是sigmoid激活
for i in reversed(range(1,layers)):
grades["dz"+str(i)] = parameters["w"+str(i+1)].T.dot(grades["dz"+str(i+1)]) * sigmoid_prime(caches["z"][i])
grades["dw"+str(i)] = grades["dz"+str(i)].dot(caches["a"][i-1].T)/m
grades["db"+str(i)] = np.sum(grades["dz"+str(i)],axis = 1,keepdims = True) /m
return grades
# 就是把其所有的权重以及偏执都更新一下
def update_grades(parameters,grades,learning_rate):
layers = len(parameters)//2
for i in range(1,layers+1):
parameters["w"+str(i)] -= learning_rate * grades["dw"+str(i)]
parameters["b"+str(i)] -= learning_rate * grades["db"+str(i)]
return parameters
# 计算误差值
def compute_loss(al,y):
return np.mean(np.square(al-y))
# 加载数据
def load_data():
"""
加载数据集
"""
x = np.arange(0.0,1.0,0.01)
y =20* np.sin(2*np.pi*x)
# 数据可视化
plt.scatter(x,y)
return x,y
#进行测试
x,y = load_data()
x = x.reshape(1,100)
y = y.reshape(1,100)
plt.scatter(x,y)
parameters = init_parameters([1,25,1])
al = 0
for i in range(4000):
caches,al = forward(x, parameters)
grades = backward(parameters, caches, al, y)
parameters = update_grades(parameters, grades, learning_rate= 0.3)
if i %100 ==0:
print(compute_loss(al, y))
plt.scatter(x,al)
plt.show()
手撕单头注意力机制(ScaledDotProductAttention)函数
输入是query和 key-value,注意力机制首先计算query与每个key的关联性(compatibility),每个关联性作为每个value的权重(weight),各个权重与value的乘积相加得到输出。
class ScaledDotProductAttention(nn.Module):
""" Scaled Dot-Product Attention """
def __init__(self, scale):
super().__init__()
self.scale = scale
self.softmax = nn.Softmax(dim=2)
def forward(self, q, k, v, mask=None):
u = torch.bmm(q, k.transpose(1, 2)) # 1.Matmul
u = u / self.scale # 2.Scale
if mask is not None:
u = u.masked_fill(mask, -np.inf) # 3.Mask
attn = self.softmax(u) # 4.Softmax
output = torch.bmm(attn, v) # 5.Output
return attn, output
if __name__ == "__main__":
n_q, n_k, n_v = 2, 4, 4
d_q, d_k, d_v = 128, 128, 64
q = torch.randn(batch, n_q, d_q)
k = torch.randn(batch, n_k, d_k)
v = torch.randn(batch, n_v, d_v)
mask = torch.zeros(batch, n_q, n_k).bool()
attention = ScaledDotProductAttention(scale=np.power(d_k, 0.5))
attn, output = attention(q, k, v, mask=mask)
print(attn)
print(output)
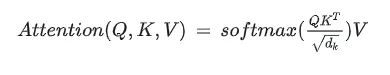
手撕多头注意力(MultiHeadAttention)
class MultiHeadAttention(nn.Module):
""" Multi-Head Attention """
def __init__(self, n_head, d_k_, d_v_, d_k, d_v, d_o):
super().__init__()
self.n_head = n_head
self.d_k = d_k
self.d_v = d_v
self.fc_q = nn.Linear(d_k_, n_head * d_k)
self.fc_k = nn.Linear(d_k_, n_head * d_k)
self.fc_v = nn.Linear(d_v_, n_head * d_v)
self.attention = ScaledDotProductAttention(scale=np.power(d_k, 0.5))
self.fc_o = nn.Linear(n_head * d_v, d_o)
def forward(self, q, k, v, mask=None):
n_head, d_q, d_k, d_v = self.n_head, self.d_k, self.d_k, self.d_v
batch, n_q, d_q_ = q.size()
batch, n_k, d_k_ = k.size()
batch, n_v, d_v_ = v.size()
q = self.fc_q(q) # 1.单头变多头
k = self.fc_k(k)
v = self.fc_v(v)
q = q.view(batch, n_q, n_head, d_q).permute(2, 0, 1, 3).contiguous().view(-1, n_q, d_q)
k = k.view(batch, n_k, n_head, d_k).permute(2, 0, 1, 3).contiguous().view(-1, n_k, d_k)
v = v.view(batch, n_v, n_head, d_v).permute(2, 0, 1, 3).contiguous().view(-1, n_v, d_v)
if mask is not None:
mask = mask.repeat(n_head, 1, 1)
attn, output = self.attention(q, k, v, mask=mask) # 2.当成单头注意力求输出
output = output.view(n_head, batch, n_q, d_v).permute(1, 2, 0, 3).contiguous().view(batch, n_q, -1) # 3.Concat
output = self.fc_o(output) # 4.仿射变换得到最终输出
return attn, output
if __name__ == "__main__":
n_q, n_k, n_v = 2, 4, 4
d_q_, d_k_, d_v_ = 128, 128, 64
q = torch.randn(batch, n_q, d_q_)
k = torch.randn(batch, n_k, d_k_)
v = torch.randn(batch, n_v, d_v_)
mask = torch.zeros(batch, n_q, n_k).bool()
mha = MultiHeadAttention(n_head=8, d_k_=128, d_v_=64, d_k=256, d_v=128, d_o=128)
attn, output = mha(q, k, v, mask=mask)
print(attn.size())
print(output.size())
手撕自注意力机制函数(SelfAttention)
Self-Attention。和Attention类似,他们都是一种注意力机制。不同的是Attention是source对target,输入的source和输出的target内容不同。例如英译中,输入英文,输出中文。而Self-Attention是source对source,是source内部元素之间或者target内部元素之间发生的Attention机制,也可以理解为Target=Source这种特殊情况下的注意力机制。
class SelfAttention(nn.Module):
""" Self-Attention """
def __init__(self, n_head, d_k, d_v, d_x, d_o):
self.wq = nn.Parameter(torch.Tensor(d_x, d_k))
self.wk = nn.Parameter(torch.Tensor(d_x, d_k))
self.wv = nn.Parameter(torch.Tensor(d_x, d_v))
self.mha = MultiHeadAttention(n_head=n_head, d_k_=d_k, d_v_=d_v, d_k=d_k, d_v=d_v, d_o=d_o)
self.init_parameters()
def init_parameters(self):
for param in self.parameters():
stdv = 1. / np.power(param.size(-1), 0.5)
param.data.uniform_(-stdv, stdv)
def forward(self, x, mask=None):
q = torch.matmul(x, self.wq)
k = torch.matmul(x, self.wk)
v = torch.matmul(x, self.wv)
attn, output = self.mha(q, k, v, mask=mask)
return attn, output
if __name__ == "__main__":
n_x = 4
d_x = 80
x = torch.randn(batch, n_x, d_x)
mask = torch.zeros(batch, n_x, n_x).bool()
selfattn = SelfAttention(n_head=8, d_k=128, d_v=64, d_x=80, d_o=80)
attn, output = selfattn(x, mask=mask)
print(attn.size())
print(output.size())
手撕 beamsearch 算法
emsp;在NLP翻译或对话任务中,在句子解码阶段,经常用到一种搜索算法beam search。这个算法有时候在大厂面试中,甚至可能会被要求手写实现。这里就从beam search的原理出发,最后手写实现一个beam search。
- 思路:beam search在贪心搜索上进一步扩大了搜索范围,贪心搜索每下一步只考虑当前最优的top-1结果,beam search考虑最优的top-k个结果。
import torch
import torch.nn.functional as F
def beam_search(LM_prob,beam_size = 3):
batch,seqlen,vocab_size = LM_prob.shape
#对LM_prob取对数
log_LM_prob = LM_prob.log()
#先选择第0个位置的最大beam_size个token,log_emb_prob与indices的shape为(batch,beam)
log_beam_prob, indices = log_LM_prob[:,0,:].topk(beam_size,sorted = True)
indices = indices.unsqueeze(-1)
#对每个长度进行beam search
for i in range(1,seqlen):
#log_beam_prob (batch,beam,vocab_size),每个beam的可能产生的概率
log_beam_prob = log_beam_prob.unsqueeze(-1) + log_LM_prob[:,i,:].unsqueeze(1).repeat(1,beam_size,1)
#选择当前步概率最高的token
log_beam_prob, index = log_beam_prob.view(batch,-1).topk(beam_size,sorted = True)
#下面的计算:beam_id选出新beam来源于之前的哪个beam;index代表真实的token id
#beam_id,index (batch,beam)
beam_id = index//vocab_size
index = index%vocab_size
mid = torch.Tensor([])
#对batch内每个样本循环,选出beam的同时拼接上新生成的token id
for j,bid,idx in zip(range(batch),beam_id,index):
x = torch.cat([indices[j][bid],idx.unsqueeze(-1)],-1)
mid = torch.cat([mid,x.unsqueeze(0)],0)
indices = mid
return indices,log_beam_prob
if __name__=='__main__':
# 建立一个语言模型 LM_prob (batch,seqlen,vocab_size)
LM_prob = F.softmax(torch.randn([32,20,1000]),dim = -1)
#最终返回每个候选,以及每个候选的log_prob,shape为(batch,beam_size,seqlen)
indices,log_prob = beam_search(LM_prob,beam_size = 3)
print(indices)
手撕 k-means 算法
import numpy as np
def kmeans(data, k, thresh=1, max_iterations=100):
# 随机初始化k个中心点
centers = data[np.random.choice(data.shape[0], k, replace=False)]
for _ in range(max_iterations):
# 计算每个样本到各个中心点的距离
distances = np.linalg.norm(data[:, None] - centers, axis=2)
# 根据距离最近的中心点将样本分配到对应的簇
labels = np.argmin(distances, axis=1)
# 更新中心点为每个簇的平均值
new_centers = np.array([data[labels == i].mean(axis=0) for i in range(k)])
# 判断中心点是否收敛,多种收敛条件可选
# 条件1:中心点不再改变
if np.all(centers == new_centers):
break
# 条件2:中心点的阈值小于某个阈值
# center_change = np.linalg.norm(new_centers - centers)
# if center_change < thresh:
# break
centers = new_centers
return labels, centers
# 生成一些随机数据作为示例输入
data = np.random.rand(100, 2) # 100个样本,每个样本有两个特征
# 手动实现K均值算法
k = 3 # 聚类数为3
labels, centers = kmeans(data, k)
# 打印簇标签和聚类中心点
print("簇标签:", labels)
print("聚类中心点:", centers)
手撕 Layer Normalization 算法
import torch
from torch import nn
class LN(nn.Module):
# 初始化
def __init__(self, normalized_shape, # 在哪个维度上做LN
eps:float = 1e-5, # 防止分母为0
elementwise_affine:bool = True): # 是否使用可学习的缩放因子和偏移因子
super(LN, self).__init__()
# 需要对哪个维度的特征做LN, torch.size查看维度
self.normalized_shape = normalized_shape # [c,w*h]
self.eps = eps
self.elementwise_affine = elementwise_affine
# 构造可训练的缩放因子和偏置
if self.elementwise_affine:
self.gain = nn.Parameter(torch.ones(normalized_shape)) # [c,w*h]
self.bias = nn.Parameter(torch.zeros(normalized_shape)) # [c,w*h]
# 前向传播
def forward(self, x: torch.Tensor): # [b,c,w*h]
# 需要做LN的维度和输入特征图对应维度的shape相同
assert self.normalized_shape == x.shape[-len(self.normalized_shape):] # [-2:]
# 需要做LN的维度索引
dims = [-(i+1) for i in range(len(self.normalized_shape))] # [b,c,w*h]维度上取[-1,-2]维度,即[c,w*h]
# 计算特征图对应维度的均值和方差
mean = x.mean(dim=dims, keepdims=True) # [b,1,1]
mean_x2 = (x**2).mean(dim=dims, keepdims=True) # [b,1,1]
var = mean_x2 - mean**2 # [b,c,1,1]
x_norm = (x-mean) / torch.sqrt(var+self.eps) # [b,c,w*h]
# 线性变换
if self.elementwise_affine:
x_norm = self.gain * x_norm + self.bias # [b,c,w*h]
return x_norm
# ------------------------------- #
# 验证
# ------------------------------- #
if __name__ == '__main__':
x = torch.linspace(0, 23, 24, dtype=torch.float32) # 构造输入层
x = x.reshape([2,3,2*2]) # [b,c,w*h]
# 实例化
ln = LN(x.shape[1:])
# 前向传播
x = ln(x)
print(x.shape)
手撕 Batch Normalization 算法
class MyBN:
def __init__(self, momentum=0.01, eps=1e-5, feat_dim=2):
"""
初始化参数值
:param momentum: 动量,用于计算每个batch均值和方差的滑动均值
:param eps: 防止分母为0
:param feat_dim: 特征维度
"""
# 均值和方差的滑动均值
self._running_mean = np.zeros(shape=(feat_dim, ))
self._running_var = np.ones((shape=(feat_dim, ))
# 更新self._running_xxx时的动量
self._momentum = momentum
# 防止分母计算为0
self._eps = eps
# 对应Batch Norm中需要更新的beta和gamma,采用pytorch文档中的初始化值
self._beta = np.zeros(shape=(feat_dim, ))
self._gamma = np.ones(shape=(feat_dim, ))
def batch_norm(self, x):
"""
BN向传播
:param x: 数据
:return: BN输出
"""
if self.training:
x_mean = x.mean(axis=0)
x_var = x.var(axis=0)
# 对应running_mean的更新公式
self._running_mean = (1-self._momentum)*x_mean + self._momentum*self._running_mean
self._running_var = (1-self._momentum)*x_var + self._momentum*self._running_var
# 对应论文中计算BN的公式
x_hat = (x-x_mean)/np.sqrt(x_var+self._eps)
else:
x_hat = (x-self._running_mean)/np.sqrt(self._running_var+self._eps)
return self._gamma*x_hat + self._beta
手撕 二维卷积 算法
import numpy as np
def conv2d(img, in_channels, out_channels ,kernels, bias, stride=1, padding=0):
N, C, H, W = img.shape
kh, kw = kernels.shape
p = padding
assert C == in_channels, "kernels' input channels do not match with img"
if p:
img = np.pad(img, ((0,0),(0,0),(p,p),(p,p)), 'constant') # padding along with all axis
out_h = (H + 2*padding - kh) // stride + 1
out_w = (W + 2*padding - kw) // stride + 1
outputs = np.zeros([N, out_channels, out_h, out_w])
# print(img)
for n in range(N):
for out in range(out_channels):
for i in range(in_channels):
for h in range(out_h):
for w in range(out_w):
for x in range(kh):
for y in range(kw):
outputs[n][out][h][w] += img[n][i][h * stride + x][w * stride + y] * kernels[x][y]
if i == in_channels - 1:
outputs[n][out][:][:] += bias[n][out]
return outputs
-------------THE END-------------
休息一下~

文章来源于微信公众号:AIGC小白入门记 等
文章链接:
https://mp.weixin.qq.com/s/2blXYBuKlKrdLOu6VzcqvQ
https://mp.weixin.qq.com/s/8mKp63Qw24q5v1biA7i9uQ
本文仅用于学术分享,如有侵权,请联系后台作删文处理
作者:楚千羽
出处:https://www.cnblogs.com/chuqianyu/
本文来自博客园,本文作者:楚千羽,转载请注明原文链接:https://www.cnblogs.com/chuqianyu/p/18048501
本文版权归作者和博客园共有,欢迎转载,但未经作者同意必须在文章页面给出原文连接,否则保留追究法律责任的权利!


