引导滤波(guided filter)与快速引导滤波(fast guided filter)理解

最近在学习图片的滤波和去噪的相关知识，查阅了一些资料参考了一些博客，这里做一个整合＋理解。参考的博客资料在文末。

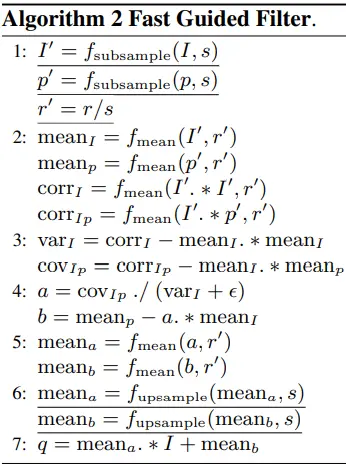
引入普通滤波的概念

假设输入图像为p，滤波窗口为wk,经过滤波后的输出图像为q,那么q图的第i个像素是由输入图p中以第i个像素为中心的窗口内的所有像素加权平均得到的，即：

从公式上来看，普通的例如均值滤波与引导滤波区别在于权重的选择上，也就是Wij(I)的不同。

引导滤波

看到的最多的引导滤波的过程图如图所示：

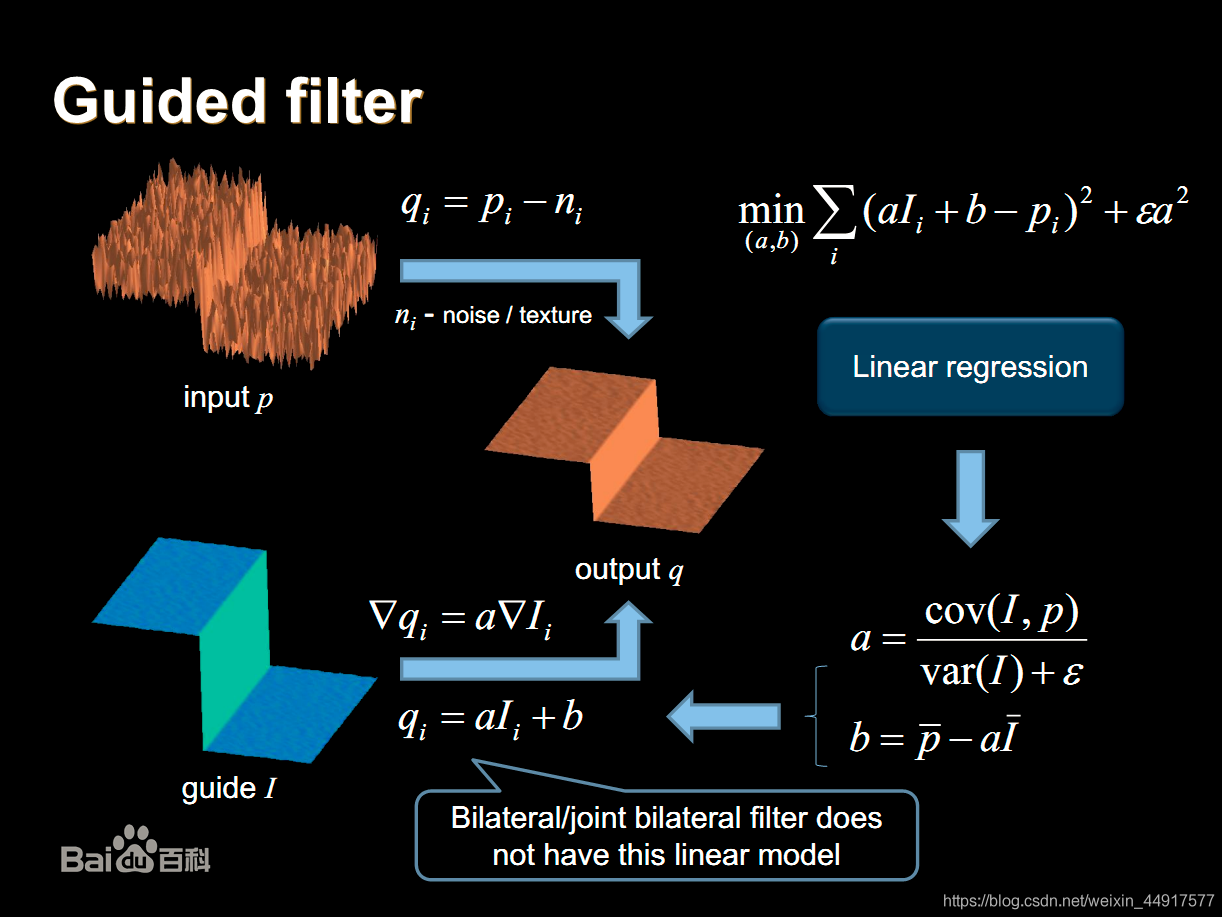
我们逐步来看这个图，首先引导滤波有两个输入，原始图p和引导图I。经过滤波后有一个输出q,滤波窗口为Wk.整个引导滤波器的表示为公式：

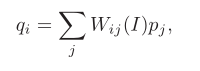
其中j∈Wk，j仅仅是在某一个窗口内的下标，Wij(I)是仅仅与引导图I相关的加权平均的那个权重。
首先我们看到引导图I，文章有一个重要的假设，就是使输入引导图I与输出图q之间是一个线性关系，表示为：

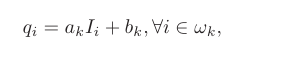
其中ak和bk表示常数参数，注意一个窗口Wk只对应一对常熟参数ak和bk。例如以第一个像素为中心的窗口W1的参数为a1,b1。以第二个像素为中心的窗口w2的参数为a2,b2.
也就是总流程图中的这一部分：

图中还对线性关系两边求导得到

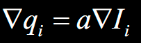
这就表示引导图的梯度变化与结果图的梯度变化是线性关系的，假设在引导图中我们知道A区是平滑区域，B区是边缘区域，显然B区梯度比A区要大，而且假设B区的梯度是A区的4倍。通过线性变换，我们得到了输出图q中的A区和B区梯度变为引导图的a倍，但是B区的梯度仍然是A区的4倍，同一幅图中的A和B之间的梯度关系没有被扭曲，通俗来讲就是引导图告诉了输出图哪里是平滑区域，哪里是边缘区域。这就是引导图的作用。
我们已知了引导图I，如果能求得系数ab的值，就可以计算出输出了。这时候就需要引入另外一个概念：噪声

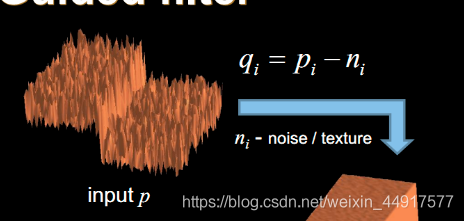
利用最小二乘法就能计算出参数a,b。

通过上述的最小二乘法可以计算出参数a,b的表达式

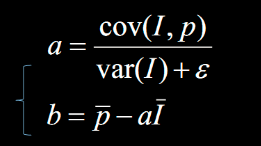
具体详细的公式推导可以参考链接：
https://blog.csdn.net/weixin_43194305/article/details/88959183
https://blog.csdn.net/HIVAN1/article/details/104722729
https://www.jianshu.com/p/36b0c8e22669
https://blog.csdn.net/qq_29788741/article/details/128865604
引导滤波与快速引导滤波肉眼没区别：https://blog.csdn.net/kuweicai/article/details/78385871
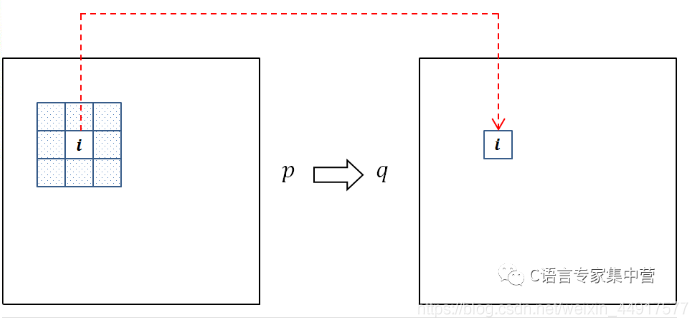
计算出了参数之后，我们就可以将线性模型应用到整个图像的滤波窗口，但一个像素会被多个窗口包含，如下图，若Wk大小为3x3，则除边缘区域的外的每个点会被包含在9个窗口里，因此对于同一个像素，会得到|w|个输出qi。

我们最后需要用的参数a,b就是所求的平均的参数a,b。
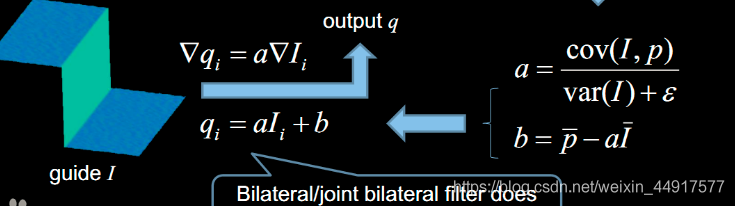
最后将参数代回线性关系公式中，就可以得到输出,过程如下图所示
**
**
matlab实现代码在这里
链接：https://github.com/accessify/fast-guided-filter

需要注意的是，boxfilter.m和guidedfilter.m。其中guidedfilter.m需要调用boxfilter.m函数，GuidedFilter_preserveEdge.m是主函数，用来调用guidedfilter函数，本代码用的输入图和引导图是同一张cat.bmp。演示的是保边效果，可以更换引导图和输入图。
————————————————
转自：https://blog.csdn.net/weixin_44917577/article/details/107186673