汉诺塔

汉诺塔—理解递归

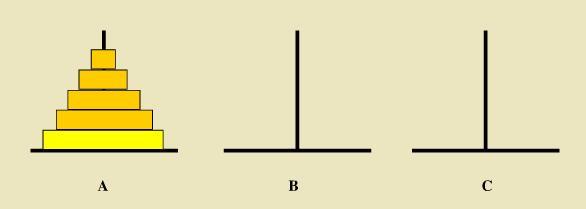
如下图所示，从左到右有A、B、C三根柱子，其中A柱子上面有从小叠到大的n个圆盘，现要求将A柱子上的圆盘移到C柱子上去，期间只有一个原则：一次只能移到一个盘子且大盘子不能在小盘子上面，求移动的步骤

Code

#include <iostream>
using namespace std;


void move(char A, char C)
{
    cout << "move a plate from " << A << " to " << C << endl;
}
/*
 * 将A中n个圆盘，借助B，全部移动到C中
 */
void hanoi(int n, char A, char B, char C)
{
    if(n == 1)
        move(A, C);
    else
    {
        //先将n-1个盘子从A上借助C移动到B
        hanoi(n-1, A, C, B);
        //再将1个(最大的盘子)从A直接移动到C
        hanoi(1, A, B, C);  //代码等同于move(A,C);
        //再将n-1个盘子从B借助A移动到C
        hanoi(n-1, B, A, C);
    }

}

int main()
{
    char A = 'A';
    char B = 'B';
    char C = 'C';
    int n = 3;
    hanoi(n, A, B, C);
}

最终的输出为

move a plate from A to C
move a plate from A to B
move a plate from C to B
move a plate from A to C
move a plate from B to A
move a plate from B to C
move a plate from A to C

借助知乎上的一个动图能够更好的理解。

此外，不难发现一个规律

• 当n=1时，只需要移动1次
• 当n=2时，需要移动3次
• 当n=3时，需要移动7次
• 当n=4时，需要移动15次
• ……
• 依此类推，当n = m时，需要移动 \(2^{m} - 1\)次