NOIP2012题目简析
chunlvxiong的博客
DAY1:
T1: Vigenere密码
简单模拟题。照着题目走就好了。无智商含量。
T2:国王游戏
这题还是比较有趣的,思考方式如下:
设第i个人左手上的数为Ai,右手上的数为Bi。
假设X排在Y前面一个位置,同时X前面的人左手数字乘积为C。
那么X获得的奖赏为C/BX,Y获得的奖赏是C*AX/BY。
如果X和Y交换位置,那么Y获得奖赏为C/BY,X获得奖赏为C*AY/BX。
C/BX-C/BY=C*(BY-BX)/(BX*BY)
C*AX/BY-C*AY/BX=C*(AX*BX-AY*BY)/(BX*BY)
由于C*AX/BY>C*BY且C*AY/BX>C/BX,说明要比较两种方法的优劣,关键是要比较C*AX/BY和C*AY/BX的大小。
从刚才的通分结果看出,如果C*AX/BY<C*AY/BX,则AX*BX<AY*BY。
然后因为这个结果是具有传递性的,所以可以作为本题的贪心策略,即按AX*BX从小到大排序是最优结果。
T3:开车旅行
首先很容易想到要预处理出距离每个城市最近的城市和距离,以及第二近的城市和距离。
但是暴力是O(N^2)的,预处理直接T掉。
这个步骤可以用如下方案解决:
1、对输入的城市高度进行离散化
2、倒着操作,开两颗线段树(以城市高度离散化后的结果为下标),一颗线段树维护区间最小值和次小值,另一颗维护区间最大值和次大值。
3、对于每个城市的距离XI,你可以把后面区间中比它大的次小值和最小值取出,以及比它小的次大值和最大值取出,然后比较得到距离其最近的城市和第二近的城市(也就是说,你的线段树还要顺带保存最值和次值对应的城市编号)。
预处理通过这样的步骤解决,复杂度是O(NlogN)的。但是问题在于线段树维护的值太多,会使得代码量大大加长。因此先不考虑如何做预处理的问题(线段树是下下之选),考虑主体部分。
询问主要是两种:
1、给定X0,询问从哪个城市出发,A行驶的距离/B行驶的距离比值最大。
2、给定XI和SI,询问A行驶的距离和B行驶的距离。
这两个算法本质差不多,我们可以把问题1视为枚举所有城市,然后求出A行驶的距离和B行驶的距离。
因为有了预处理算出来的结果,所以直接就是一步一步的枚举,复杂度O(N^2)==TLE。
不难想到可以利用倍增思想。
为了方便处理,把A走一步B走一步合称一步。
然后你就用fa[i][j]表示i号城市走1<<j步到了哪个城市,用dis_a[i][j]表示a走的距离,dis_b[i][j]表示b走的距离。
这样预处理变为了O(NlogN)的,到时候对于每个询问,你可以利用倍增优化二分(就是类似LCA的做法),在logn的时间内完成询问。
当然别忘记最后判断A还能不能再走一步。
那么问题完美的变成了:如何做预处理。
事实上,有更好的解决办法--set(P党选手请无视)。
你仍然是倒着做,然后把城市高度扔进set里面。题目说了,没有重复的高度,所以这个城市左边、左边的左边、右边、右边的右边就是最近和次近的可能城市。
然后把这四个值排个序就得到结果了(这实际上是用set完成了线段树的功能)。
然后这样预处理复杂度也是O(NlogN)的,你就可以完美的把代码控制在3K以内了。
DAY2:
T1:同余方程
求AX=1(MOD B)的最小正整数X(保证一定有解)。
把同余方程转化为线性方程,即AX-BY=1。
然后你发现这是个基础的EX_GCD问题,由于一定有解,所以GCD(A,B)=1。
然后你把得到X,Y以后把X调整成最小正整数就好了。
T2:借教室
做法一:
这道题目很容易想到线段树。首先线段树维护的每天剩余的教室数的MIN值。
然后暴力的从上往下处理每个请求,每次区间修改。
一旦发现tree[1].min<0,说明不对头了,表示这个请求出问题了。
复杂度O(NlogN),由于O(2e7)的复杂度+线段树自带大常数,这个算法理论上有可能被卡。
然而洛谷上交了一发A掉了。
做法二:
第几个请求出了问题,让人联想到二分答案。
那么怎么验证呢?
可以逐个处理问题,然后将区间修改。
最后O(N)横扫判断有没有一天的教室数大于了最多能供给的教室数。
问题在于这个区间求改的复杂度。
如果仍然用线段树O(logN)的复杂度,那么T掉而且还不如去写做法一。
这里你要考虑差分优化,这实际上是一个经典的技术。
就是你先令B[X]=A[X]-A[X-1]。然后A[X]..A[Y]全部加Z,就转变成了B[X]+Z,B[Y+1]-Z。
然后你维护这个B数组就好了,是O(1)的。
最后O(N)计算前缀和得到原值,就可以用于判断了。
时间复杂度一样O(NlogN),但是常数小,跑出来确实比线段树快。
T3:疫情控制
控制疫情的最小时间-->二分答案。
然后比较好发现的是,对于一个军队,如果他在规定时间内到达不了根节点,肯定是到达他能到达的最上面的城市就好。
那么这个东西总不可能一步一步枚举吧?
受倍增求LCA启发,可以用类似的方式在logN的时间内解决这个问题。
那么能到达根节点的军队呢怎么办呢?
首先,这种军队至多只会往下走一步(谁让首都不能驻扎军队)。
很明显到达根节点后军队的剩余时间越多,这个军队越有用。
需要注意的一点,一支军队从哪个节点走到根节点,他可以不付出任何代价驻守该节点(因为他可以不走到根节点去嘛)。
很容易想到贪心,贪心思路的第一步也都是肯定的:把标记上传,确定根的所有直接子节点的控制情况:
1、一种错误的贪心思路:
对于每个根节点:先把从这个节点到根节点的军队剩余时间最少的那支驻守在这个节点上。然后派其他军队走到根节点。接下来距离根节点最小的节点就用能到达他的剩余时间最少的军队去驻守。
反例:
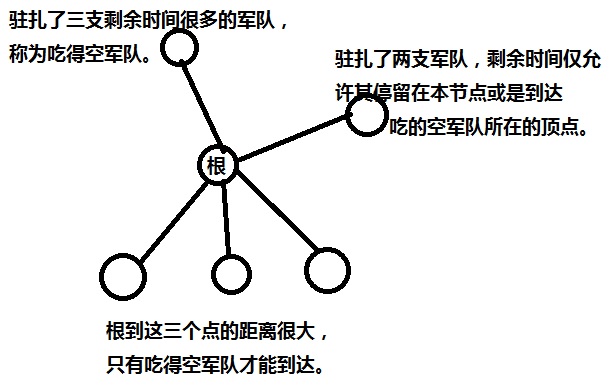
从上图可以看出,正确做法是派最右边节点的两支军队驻守上面的两个节点,派吃的空军队去驻守下面的三个空节点。
而我们的贪心则会派一支吃的空军队去驻守本节点,大大的浪费。
2、第二个错误的贪心思路:
为了解决上述问题,我们如下考虑。
先假设所有军队已经抵达了根节点,然后按剩余时间排序,同时根到所有子节点的距离也排了序。
如果剩余时间最少的节点能到达距离最近的节点,那么就驻守在那个节点,否则派他去驻守原节点。
反例:

如果下方节点的距离小于上方节点的距离,那么贪心又挂了。(然而我记得这样在洛谷上交了一发A掉了)
3、正确的贪心思路
实际上贪心思路2已经离正确方法很相近了。由于军队要发挥其最大价值,所以可以这样贪心:
1、当前军队已经废了(它连未被覆盖的距离最近的节点也去不了了),那么就把他赶回老家。
2、当前军队可以覆盖离他最近的节点,此时千万不要直接派他去那个节点。
判断:如果他老家到根的距离比这个节点大,而且他老家没被覆盖,那么把他赶回老家更能体现他的价值,因此仍然选择把他赶回老家。
反例:没有反例。
这样,就完美地解决了这个问题。





