二叉树的前序遍历之Morris
之前我们介绍了二叉树前序排序的两种方法,一种是递归,一种是迭代。这两种没有什么大的差别。今天我们带来了一种Morris遍历
Morris 遍历的核心思想是利用树的大量空闲指针,实现空间开销的极限缩减
其前序遍历规则总结如下:
1,新建临时树,令该节点为树的根;
2,如果当前根的左子树为空,将当前根放入数组,并将当前根的右子树更新为树的根;
3,如果当前根的左子树不为空,获取到当前根的左子树:
3.1, 循环遍历当前根的左子树的所有右子树,获取到最后一个不等于根的右子树
3.1, 如果获取到的右子树为空,将根节点放入数组,然后将根赋值给遍历获取到的右子树的右子树。
3.2, 如果获取到的右子树不为空,将获取到的右子树的右子树删除,同时将根的右子树更新为树的根
重复步骤 2 和步骤 3,直到遍历结束。
看到这里如果有一点点懵的话就看一下下面的图,我会一步一步的将实现过程给画出来。
第一步,我们获取到树的根F,然后获取F的左子树,如果左子树为空,我们就将F放入数组,然后获取树的右子树更新为树的根。
这里左子树不为空,我们第一步拿到树的左子树B,然后遍历B的所有右子树,一直遍历到右子树为空并且右子树不等于当前根的情况,这里我们B本来就没有右子树,所以直接拿到B。
当B的右子树为空,我们将F放入数组。然后将F放入B的右子树。
根节点指向B
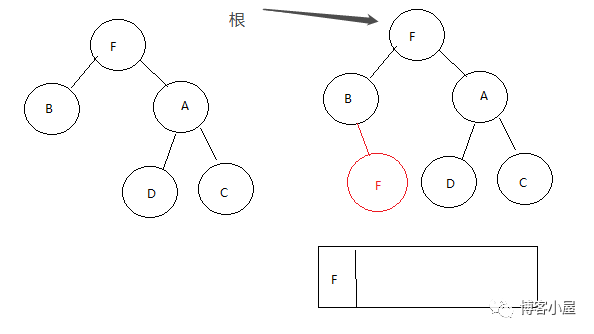
第二步,我们获取到树的根 B,判断B的左子树,如果左子树为空,我们将就将B 放入数组,同时将根指向 F
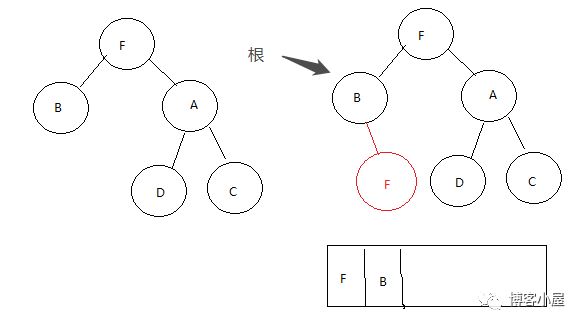
第三步,我们获取到树的根F,判断F的左子树是否为空,这里树的左子树不为空,所以拿到树的左子树B ,然后遍历B的所有右子树,一直遍历到右子树为空并且右子树不等于根的情况。
这里B的右子树是等于根的,所以走恢复二叉树的逻辑,将B的右子树 清空,同时将根指向根的右子树 A
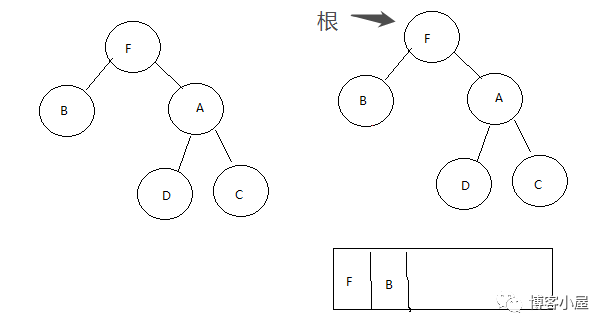
第四步,我们获取到树的根A,判断A的左子树是否为空,这里树的左子树不为空,所以拿到树的左子树D,然后遍历D的所有右子树,一直遍历到右子树为空并且右子树不等于当前根的情况,这里我们的D本来就没有右子树,所以直接拿到D ,因为D的右子树为空,那么我们将根A放入到数组,将根A放入到D的右子树。根节点指向D
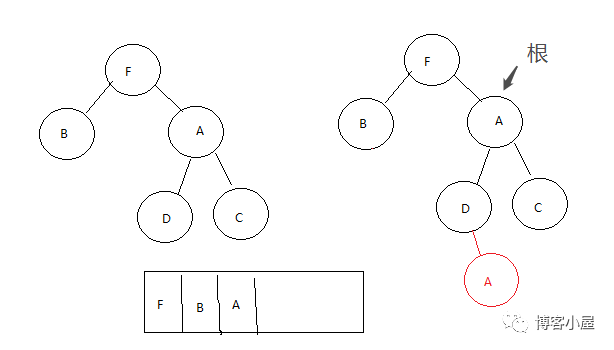
第五步,我们获取到树的根D,判断D的左子树,如果D的左子树为空,那么将D放入数组,同时将根指向A
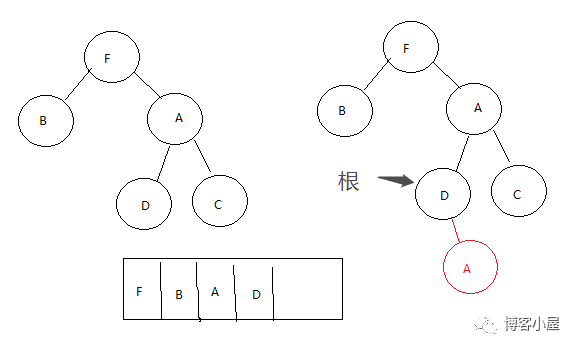
第六步,我们获取到树的根A,判断A的左子树是否为空,这里A的左子树是不为空的,所以拿到A的左子树D,然后遍历D的所有右子树,一直到右子树为空并且右子树不等于根,这里D的右子树等于根,我们走恢复二叉树逻辑,将D的右子树A删除,然后将根指向A的右子树C
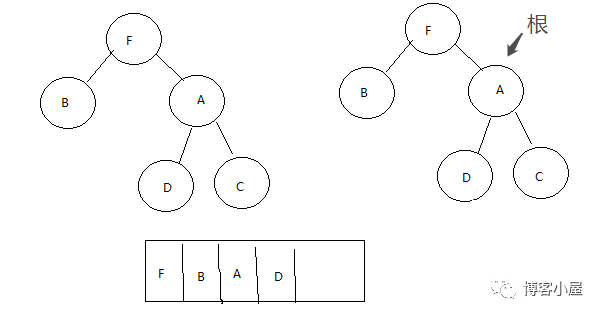
第七步,我们获取到树的根C,判断C的左子树是否为空,这里C的左子树为空,那么将C放入数组,同时将根指向C的右子树,C的右子树为空遍历结束
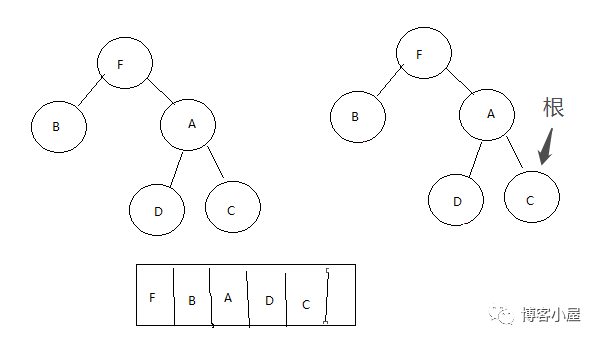
经过我们一步一步的拆解,是不是已经感觉这个排序也超级简单呢,现在上代码
public static void main(String[] args) {
Solution solution = new Solution();
TreeNode t = new TreeNode("F", new TreeNode("B",null,null), new TreeNode("A", new TreeNode("D",null,null), new TreeNode("C",null,null)));
System.out.println(Morris_PreOrder(t));
}
public static List<String> Morris_PreOrder(TreeNode root) {
List<String> res = new ArrayList<>();
if(root == null){
return res;
}
TreeNode cur = root;
while(cur != null) {
if(cur.left == null) {
res.add(cur.val);
cur = cur.right;
} else {
TreeNode tmp = cur.left;
while(tmp.right != null && tmp.right != cur){
tmp = tmp.right;
}
if(tmp.right == null) {
res.add(cur.val); //输出当前节点
tmp.right = cur; //将当前根节点赋值给 最右子树的右子树
cur = cur.left;
} else {
tmp.right = null; //恢复二叉树
cur = cur.right;
}
}
}
return res;
}
是春风, 是余晖, 是一道曙光, 是未来可期。
手敲不易,点个赞呗





