Petya and Graph/最大权闭合子图、最小割

原题地址：https://codeforces.com/contest/1082/problem/G

G. Petya and Graph

time limit per test

2 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

Petya has a simple graph (that is, a graph without loops or multiple edges) consisting of nn vertices and mm edges.

The weight of the ii-th vertex is aiai.

The weight of the ii-th edge is wiwi.

A subgraph of a graph is some set of the graph vertices and some set of the graph edges. The set of edges must meet the condition: both ends of each edge from the set must belong to the chosen set of vertices.

The weight of a subgraph is the sum of the weights of its edges, minus the sum of the weights of its vertices. You need to find the maximum weight of subgraph of given graph. The given graph does not contain loops and multiple edges.

Input

The first line contains two numbers nn and mm (1≤n≤103,0≤m≤1031≤n≤103,0≤m≤103) - the number of vertices and edges in the graph, respectively.

The next line contains nn integers a1,a2,…,ana1,a2,…,an (1≤ai≤1091≤ai≤109) - the weights of the vertices of the graph.

The following mm lines contain edges: the ii-e edge is defined by a triple of integers vi,ui,wivi,ui,wi (1≤vi,ui≤n,1≤wi≤109,vi≠ui1≤vi,ui≤n,1≤wi≤109,vi≠ui). This triple means that between the vertices vivi and uiui there is an edge of weight wiwi. It is guaranteed that the graph does not contain loops and multiple edges.

Output

Print one integer — the maximum weight of the subgraph of the given graph.

Examples

input

4 5
1 5 2 2
1 3 4
1 4 4
3 4 5
3 2 2
4 2 2

output

8

input

3 3
9 7 8
1 2 1
2 3 2
1 3 3

output

0

Note

In the first test example, the optimal subgraph consists of the vertices 1,3,41,3,4 and has weight 4+4+5−(1+2+2)=84+4+5−(1+2+2)=8. In the second test case, the optimal subgraph is empty.

 

 题意：一个有n个点m条边的图，每个点有相应的点权值，边有边权值。让你选择一些边，使得所选边权值总和减去所选边的端点的点权值总和的结果最大。

 

思路：

神奇网络流，将源点s向所有点连边，边权为点的权值，对于每条边，把它也看做一个点，并将它的两个端点与它连边，边权为无穷大，再将他与汇点t连边，边权为原来的边权。

设s、t为源点和汇点

对于边（id，u，v,  w）id表示第几条边，u、v表示它的两个端点，w表示边权,weight[u]表示点u的权值

add（s，u，weight[u]）,add（s，v，weight[v]）,add(u,id+n,inf),  add(v,id+n,inf),  add(id+n,t,w)（id+n是为了避免点和边重合了）

 

 

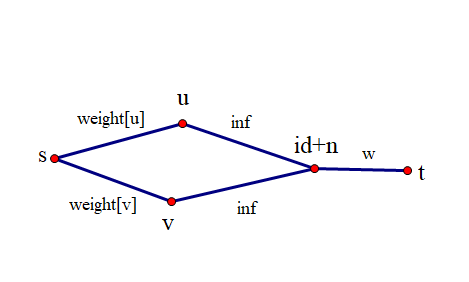
对于一条边，如果它的边权大于他两个端点的点权之和，那么就要减去它的两个端点点权之和，反之则舍弃掉这条边。

所以答案就是所有边的边权之和减去最小割。

 

代码：

#include<bits/stdc++.h>

#define closeSync ios::sync_with_stdio(0);cin.tie(0);cout.tie(0)
#define multiCase int T;cin>>T;for(int t=1;t<=T;t++)
#define rep(i,a,b) for(int i=a;i<=b;i++)
#define repp(i,a,b) for(int i=a;i<b;i++)
#define per(i,a,b) for(int i=a;i>=b;i--)
#define perr(i,a,b) for(int i=a;i>b;i--)
#define pb push_back
#define eb push_back
#define mst(a,b) memset(a,b,sizeof(a))
using namespace std;

typedef long long ll;
typedef unsigned long long ull;
typedef pair<int,int> P;
const int INF=0x3f3f3f3f;
const ll LINF=0x3f3f3f3f3f3f3f3f;
const double eps=1e-12;
const double PI=acos(-1.0);
const double angcst=PI/180.0;
const ll mod=998244353;
ll max_3(ll a,ll b,ll c){if(a>b&&a>c)return a;if(b>c)return b;return c;}
ll min_3(ll a,ll b,ll c){if(a<b&&a<c)return a;if(b<c)return b;return c;}
ll gcd(ll a,ll b){return b==0?a:gcd(b,a%b);}
ll lcm(ll a,ll b){return a/gcd(a,b)*b;}
ll qpow(ll a,ll n){ll r=1;while(n){if(n&1)r=(r*a)%mod;n>>=1;a=(a*a)%mod;}return r;}
ll qmul(ll a,ll b){ll s=(long double)a/mod*b;s=a*b-s*mod;if(s<0)s+=mod;if(s>=mod)s-=mod;return s;}


template <typename _Tp> inline _Tp read(_Tp&x){
    char c11=getchar(),ob=0;x=0;
    while(c11^'-'&&!isdigit(c11))c11=getchar();if(c11=='-')c11=getchar(),ob=1;
    while(isdigit(c11))x=x*10+c11-'0',c11=getchar();if(ob)x=-x;return x;
}
int n,m;



const int maxn=200010;
struct edge
{
    ll v,cost,rev;//边的终点、边权、反向边
};
vector<edge>g[20*maxn];//vector存图
ll deep[maxn];//表示源点到当前顶点的深度
ll iter[maxn];//当前弧，在其之前的边已经没有用了，避免了搜寻已经增广过的路径

void add(ll u,ll v,ll cost)//加边
{
    g[u].pb((edge){v,cost,g[v].size()});
    g[v].pb((edge){u,0,g[u].size()-1});
}
void bfs(int s)//建立分层网络，通过bfs计算从源点出发的距离标号
{
    mst(deep,-1);
    queue<int>q;
    deep[s]=0;//源点深度为0
    q.push(s);
    while(!q.empty())
    {
        int v=q.front();q.pop();
        for(int i=0;i<g[v].size();i++)
        {
            edge &e=g[v][i];
            if(e.cost>0&&deep[e.v]==-1)//如果还有容量能够到达i，并且i节点的深度未被标记
            {
                deep[e.v]=deep[v]+1;
                q.push(e.v);
            }
        }
    }
}
ll dfs(ll v,ll t,ll f)//基于分层网络，通过dfs寻找增广路,x表示当前节点，f表示当前这条增广路径上的最小流量
{
    if(v==t)return f;//找到汇点，返回
    for(ll &i=iter[v];i<g[v].size();i++)
    {
        edge &e=g[v][i];
        if(e.cost>0&&deep[v]<deep[e.v])//找到能从v流通过去的相邻顶点
        {
            ll d=dfs(e.v,t,min(f,e.cost));
            if(d>0)
            {
                e.cost-=d;//更新残余网络
                g[e.v][e.rev].cost+=d;//反向边
                return d;
            }
        }
    }
    return 0;//搜不到增广路径就返回0
}
ll dinic(ll s,ll t)//求s到t的最大流
{
    ll flow=0;
    while(1)
    {
        bfs(s);
        if(deep[t]<0)return flow;//不存在分层网络，算法结束
        mst(iter,0);
        ll f;
        while((f=dfs(s,t,INF))>0)
            flow+=f;
    }
}


int main()
{
    ll sum=0;
    read(n);read(m);
    ll s=0,t=1+n+m,a;
    rep(i,1,n)
    {
        read(a);
        add(s,i,a);
    }
    rep(i,1,m)
    {
        ll u,v,w;
        read(u);read(v);read(w);
        add(u,i+n,LINF);
        add(v,i+n,LINF);
        add(i+n,t,w);
        sum+=w;
    }
    printf("%lld\n",sum-dinic(s,t));
    return 0;
}