HDU 6808 Go Running(利用网络流求二分图的最小顶点覆盖、dinic）

原题地址：http://acm.hdu.edu.cn/showproblem.php?pid=6808

本文主要参考的博客：https://www.cnblogs.com/stelayuri/p/13405914.html

Go Running

Time Limit: 10000/5000 MS (Java/Others) Memory Limit: 524288/524288 K (Java/Others)
Total Submission(s): 1358 Accepted Submission(s): 500

Problem Description

Zhang3 is the class leader. Recently she's implementing a policy about long-distance running. This forces every student in her class to take a run.

There is a main road in the school from west to east, which can be regarded as an infinite axis, and its positive direction is east. Positions on the road are represented with numbers. In order to complete the task, each student must run along the main road. Each student can decide the following things:

- The time to start running.
- The time to finish running.
- The position to start running.
- The direction of running, which is either west or east.

Once these things are decided, the student will appear at the starting position on the road at the start time, then start running in the chosen direction at a speed of

Input

The first line of the input gives the number of test cases,

Output

For each test case, print a line with an integer, representing the minimum number of students who have run.

Sample Input

2 3

1 1

2 2

3 1

1 1

2 2

3 3

Sample Output

Source

2020 Multi-University Training Contest 4

题意：在一个数轴上有一些学生在跑步，跑步速度为1m每秒，但是你不知道他们的跑步方向（向左或者向右），现在给你一些点和对应的时间（可能多个点对应的是同一个人），问你最少有多少人在跑步。

思路：把所有的点投影在x-t坐标系中，容易发现，题目问你的就是最少选取多少斜率为1或-1的直线可以覆盖所有的点

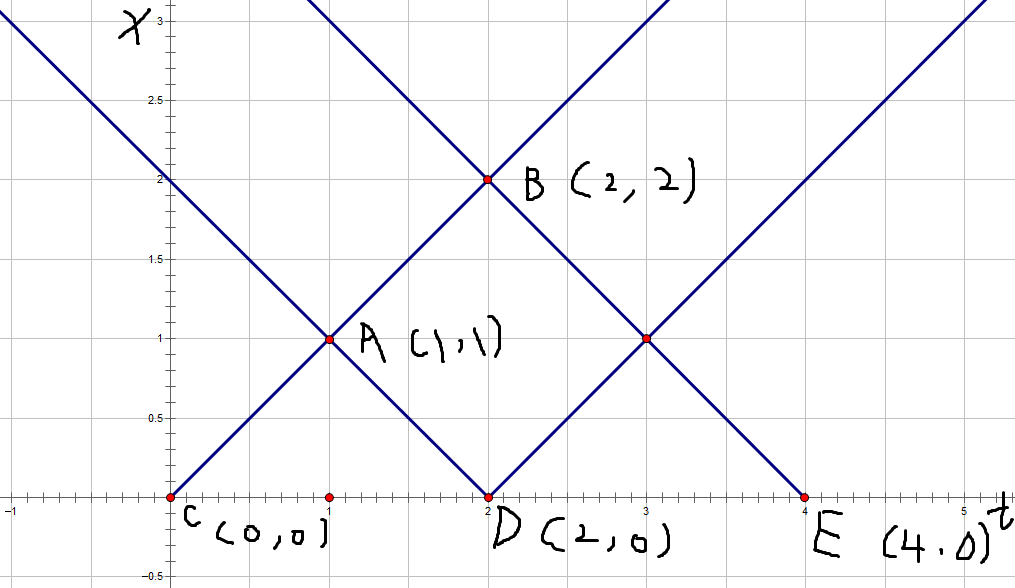
如图：A、B是你用题目里给你的两个点，用x-t代表斜率为1的集合，x+t代表斜率为-1的集合，通俗点讲，比如所有在通过点A且斜率为1的直线上的点都可以斜着投影到C点（斜率为1的情况下），同理所有在通过点A且斜率为-1的直线上的点都可以斜着投影到D点（斜率为-1的情况下），这样就好办了，将源点连向所有的x-t（x-t预处理出来后只能连一次边，x+t同理，不然就重复连了），边权为1，所有的x+t连向汇点，边权为1，x-t和x+t间再连一条边权为无穷的边（因为x-t和x+t实际上是同一个人），这样就可以通过跑最大流来求解原来的问题了。

还是如上图，设ss为源点，tt为汇点

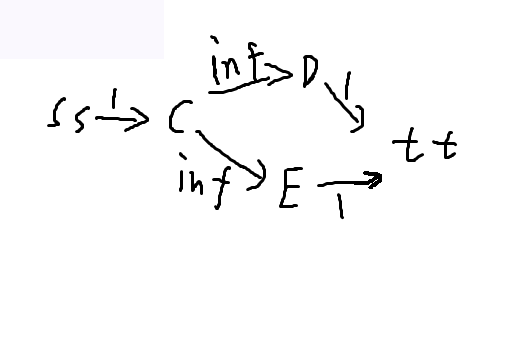
由于初始化ss->c的流量为1，所以走到tt是流量也只有1，换句话说也就是ss通过C只能走一条路到达tt吧。

代码：

#include<cstdio>
#include<cstring>
#include<cmath>
#include<cctype>
#include<iostream>
#include<sstream>
#include<algorithm>
#include<map>
#include<vector>
#include<set>
#include<stack>
#include<queue>
#include<string>
#include<utility>
#include<functional>

#define closeSync ios::sync_with_stdio(0);cin.tie(0);cout.tie(0)
#define multiCase int T;cin>>T;for(int t=1;t<=T;t++)
#define rep(i,a,b) for(int i=a;i<=b;i++)
#define repp(i,a,b) for(int i=a;i<b;i++)
#define per(i,a,b) for(int i=a;i>=b;i--)
#define perr(i,a,b) for(int i=a;i>b;i--)
#define pb push_back
#define eb push_back
#define mst(a,b) memset(a,b,sizeof(a))
using namespace std;

typedef long long ll;
typedef unsigned long long ull;
typedef pair<int,int> P;
const int INF=0x3f3f3f3f;
const ll LINF=0x3f3f3f3f3f3f3f3f;
const double eps=1e-12;
const double PI=acos(-1.0);
const double angcst=PI/180.0;
const ll mod=998244353;
ll max_3(ll a,ll b,ll c){if(a>b&&a>c)return a;if(b>c)return b;return c;}
ll min_3(ll a,ll b,ll c){if(a<b&&a<c)return a;if(b<c)return b;return c;}
ll gcd(ll a,ll b){return b==0?a:gcd(b,a%b);}
ll lcm(ll a,ll b){return a/gcd(a,b)*b;}
ll qpow(ll a,ll n){ll r=1;while(n){if(n&1)r=(r*a)%mod;n>>=1;a=(a*a)%mod;}return r;}
ll qmul(ll a,ll b){ll s=(long double)a/mod*b;s=a*b-s*mod;if(s<0)s+=mod;if(s>=mod)s-=mod;return s;}


template <typename _Tp> inline _Tp read(_Tp&x){
    char c11=getchar(),ob=0;x=0;
    while(c11^'-'&&!isdigit(c11))c11=getchar();if(c11=='-')c11=getchar(),ob=1;
    while(isdigit(c11))x=x*10+c11-'0',c11=getchar();if(ob)x=-x;return x;
}





const int maxn=666666;
struct edge
{
    int v,cost,rev;//边的终点、边权、反向边
};
vector<edge>g[maxn<<1];//vector存图
int deep[maxn];//表示源点到当前顶点的深度
int iter[maxn];//当前弧，在其之前的边已经没有用了，避免了搜寻已经增广过的路径

void add(int u,int v,int cost)//加边
{
    g[u].pb((edge){v,cost,g[v].size()});
    g[v].pb((edge){u,0,g[u].size()-1});
}
void bfs(int s)//建立分层网络，通过bfs计算从源点出发的距离标号
{
    mst(deep,-1);
    queue<int>q;
    deep[s]=0;//源点深度为0
    q.push(s);
    while(!q.empty())
    {
        int v=q.front();q.pop();
        for(int i=0;i<g[v].size();i++)
        {
            edge &e=g[v][i];
            if(e.cost>0&&deep[e.v]==-1)//如果还有容量能够到达i，并且i节点的深度未被标记
            {
                deep[e.v]=deep[v]+1;
                q.push(e.v);
            }
        }
    }
}
int dfs(int v,int t,int f)//基于分层网络，通过dfs寻找增广路,x表示当前节点，f表示当前这条增广路径上的最小流量
{
    if(v==t)return f;//找到汇点，返回
    for(int &i=iter[v];i<g[v].size();i++)
    {
        edge &e=g[v][i];
        if(e.cost>0&&deep[v]<deep[e.v])//找到能从v流通过去的相邻顶点
        {
            int d=dfs(e.v,t,min(f,e.cost));
            if(d>0)
            {
                e.cost-=d;//更新残余网络
                g[e.v][e.rev].cost+=d;//反向边
                return d;
            }
        }
    }
    return 0;//搜不到增广路径就返回0
}
int dinic(int s,int t)//求s到t的最大流
{
    int flow=0;
    while(1)
    {
        bfs(s);
        if(deep[t]<0)return flow;//不存在分层网络，算法结束
        mst(iter,0);
        int f;
        while((f=dfs(s,t,INF))>0)
            flow+=f;
    }
}
int X[111111],T[111111];
int a[222222],cnt;
int s,t;
void init()
{
    rep(i,1,2*cnt+2)g[i].clear();
    s=2*cnt+1;t=2*cnt+2;
}
void solve()
{
    int n;
    cin>>n;
    cnt=0;
    rep(i,1,n)
    {
        cin>>T[i]>>X[i];
        a[++cnt]=X[i]-T[i];
        a[++cnt]=X[i]+T[i];
    }
    sort(a+1,a+1+cnt);
    cnt=unique(a+1,a+cnt+1)-a-1;
    init();
    rep(i,1,n)
    {
        int x=lower_bound(a+1,a+cnt+1,X[i]-T[i])-a;
        int y=lower_bound(a+1,a+cnt+1,X[i]+T[i])-a;
        add(x,y+cnt,INF);
    }
    rep(i,1,cnt)
    add(s,i,1),add(i+cnt,t,1);
    cout<<dinic(s,t)<<'\n';
}
int main()
{
    closeSync;
    int TT;cin>>TT;
    while(TT--)
        solve();
    return 0;
}

posted @ 2020-08-08 21:18 chuliyou 阅读(177) 评论(1) 编辑收藏举报

刷新页面返回顶部

chuliyou

HDU 6808 Go Running(利用网络流求二分图的最小顶点覆盖、dinic）

Go Running

公告