打卡2

问题描述：

假设银行整存整取存款的不同期限的月息利益为：

0.63%，期限为1年

0.66%，2年

0.69%，3年

0.75%，5年

0.84%，8年

现在已知某人手上有2000元，要求通过计算选择出一种存钱方案，使得这笔钱存入银行20年后获得的利息最多，假定银行对超出存款期限的那部分时间不付利息。

流程图：

 

 

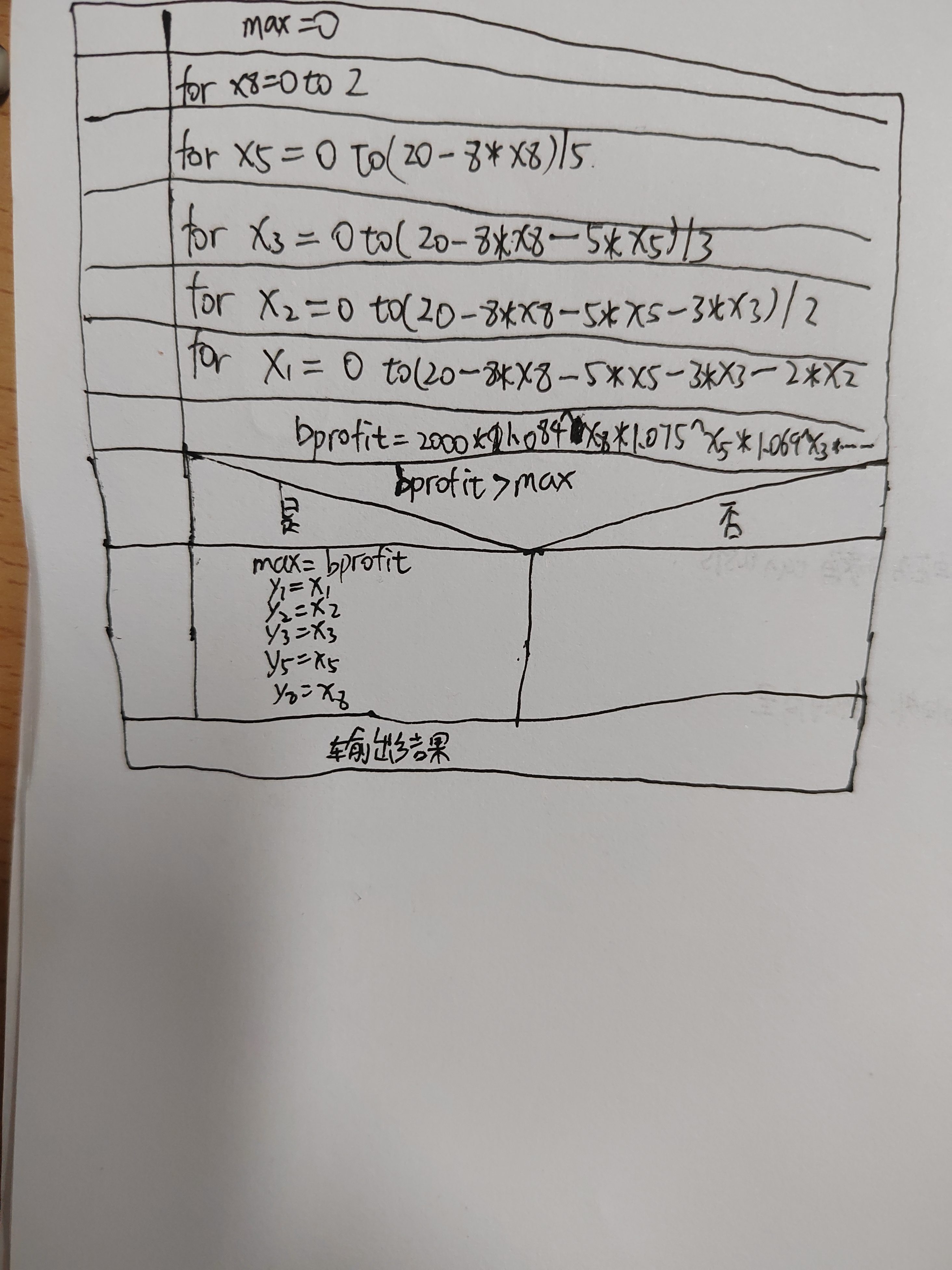
伪代码：

max=0

for x8<-0 to 2

for x5<-0 to (20-x8*8)/5

for x3<-0 to (20-x8*8-x5*5)/3

for x2<-0 to (20-x8*8-x5*5-x3*3)/2

for x1<-0 to 20-x8*8-x5*5-x3*3-x2*2

bprofit<-2000*(1+0.0084*8*12)^x8*(1+0.0075*5*12^x5*(1+0.0069*3*12)^x3*(1+0.0066*2*12)^x2*(1+0.0063*12)^x1

if max<bprofit

max<-bprofit

y1<-x1

y2<-x2

y3<-x3

y5<-x5

y8<-x8

output y1,y2,y3,y5,y8,max

代码：

#include <iostream>

#include <cmath>

using namespace std;

int main()

{

int x1,x2,x3,x5,x8,y1,y2,y3,y5,y8;

double max=0,bprofit;

for(x8=0;x8<=2;x8++)

{

for(x5=0;x5<=(20-x8*8)/5;x5++)

{

for(x3=0;x3<=(20-x8*8-x5*5)/3;x3++)

{

for(x2=0;x2<=(20-x8*8-x5*5-x3*3)/2;x2++)

{

for(x1=0;x1<=20-x8*8-x5*5-x3*3-x2*2;x1++)

{

bprofit=2000*pow(1+0.0084*8*12,x8)*pow(1+0.0075*5*12,x5)*pow(1+0.0069*3*12,x3)*pow(1+0.0066*2*12,x2)*pow(1+0.0063*12,x1);

if(bprofit>max)

{

max=bprofit;

y1=x1;

y2=x2;

y3=x3;

y5=x5;

y8=x8;

}

}

}

}

}

}

cout<<"1年"<<y1<<"次，"<<"2年"<<y2<<"次，"<<"3年"<<y3<<"次，"<<"5年"<<y5<<"次，"<<"8年"<<y8<<"次"<<endl<<"本息"<<max;

}