X Wing 数独Sudoku
https://www.learn-sudoku.com/x-wing.html
X Wing
An X Wing is a technique for removing candidates (pencil marks).
It starts with either two parallel rows or two parallel columns. Blocks are not involved here.
If you can find a row that contains the same pencil mark in exactly two spots, as well as another parallel row that mirrors it – containing the same pencil mark in only the same two spots, then you can use this information to eliminate similar pencil marks in the columns passing through those spots.
I know…that’s a mouthful. Let me illustrate. Here we see a row containing exactly two 4s:

Next, if we zoom out a bit, we can see that another row, two rows down, has the same two 4s, and in the same two spots:
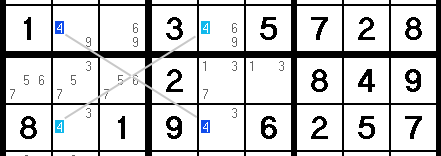
Now if we think about this, we know that each of these rows has to have a 4, right? And we also know the 4s cannot be on top of each other, because that would put two 4s in the same column.
Because of this, we can safely assume that either the light blue cells or the dark blue cells must be 4s.
Armed with this, let’s zoom out all the way and shift our focus to the columns involved here (indicated with arrows below). Based on what we said above, the 4s in these columns must exist where these two rows cross - that is, where the blue 4s are.
Knowing that, all other 4s in the columns are not possible, and can be erased (erase all the pink 4s).
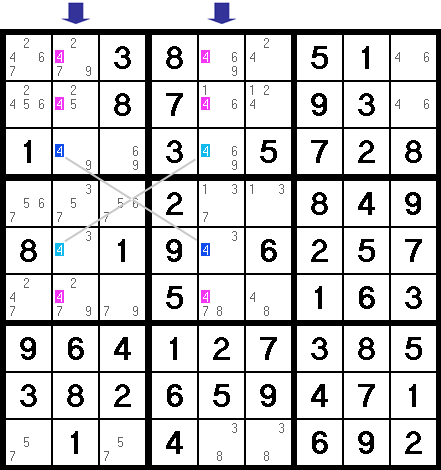
Again, this is one of those hard to find methods. In Sudoklue, the same pencil mark highlighting feature that helps me find hidden singles and omissions, can make X Wings easier to spot as well.
Of course, this whole concept can be rotated. If you can find two columns with only two identical positions for a given pencil mark, then the corresponding rows intersecting these positions can have all other candidates safely removed.
配置

下面这个,必须使用X-Wing来处理,点一下Hint,会提示

可以generate candidates来生成备选的

https://www.sudokuoftheday.com/techniques/x-wings/
X-Wings are fairly easy to spot, but a little harder to understand than some other techniques. Like others it relies on using positions of pencilmarks to infer enough to allow you to eliminate some other candidates.
X-Wings are when there are two lines, each having the same two positions for a number.
Take a look at this puzzle:

Once you’ve satisfied yourself that there aren’t any easy methods you can apply to move forward, take a look at the candidate positions for 6, in rows 4 and 9.

The trick to understanding X-Wings is to imagine what would happen if you chose just one of those positions – what would it do to the others?
Imagine making the top left of those cells be the 6 – it would force the
other candidate out on its row, and also force the candidate in the
bottom left out too (the red arrows).”,

In turn, this would force the final cell to also be a 6 (the green arrow)

So a 6 in the top left cell, would force the bottom right cell to also be a 6:

By exactly the same logic, a 6 in the top right cell would force the bottom left cell to be a 6.

See how these two forcing lines form an X? That’s how the technique got its name.
OK, I get the name, now what good does it do me?

If you think about it, whichever position 6 occupies in the top row, forces the other to occupy the opposite position in the bottom row.
Here’s the clever bit – even though you don’t know which row has the 6
at the left, and which row has the 6 at the right, you know for sure that both will be occupied
And because you know that the 6 will definitely be in both of those two
column positions, you can look up and down those columns, and remove any
other candidates!
We can’t remove any 6s from the left hand column this time, but there are two we can remove from the right hand column, and one of those leaves an 8 as a single candidate!
What is new about this technique is that knowledge about two (similar) rows, lets you make removals from columns. Of course, it works the other way too, if you can spot similar columns.
You’ll often spot X-Wings – they are quite common, but they won’t always lead to you being able to remove candidates.
Tip
The trick to spotting X-Wings is to look for the rectangles of possible candidates. If you find four candidates on the corners of a rectangle, check to see if they are an X-Wing for both rows and columns – that might save you some extra time!
Some more examples
X-Wing in rows for 8.

X-Wing in rows for 9.

X-Wing in rows for 4.

https://www.sudokuessentials.com/x-wing.html
https://www.sudokuessentials.com/sudoku_tips.html
Learn the Sudoku X-Wing to solve some tough puzzles.
Learn the Sudoku XY-Wing to solve more tough puzzles.
Learn the Sudoku Swordfish pattern to solve some tougher puzzles.
Try this brain teaser to solve some difficult puzzles.
https://www.sudokuessentials.com/sudoku-puzzle-solver.html
http://angusj.com/sudoku/ 下载到本地
https://github.com/tropicalwzc/ice_sudoku.github.io/releases
作者:Chuck Lu GitHub |




【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 记一次.NET内存居高不下排查解决与启示
· 探究高空视频全景AR技术的实现原理
· 理解Rust引用及其生命周期标识(上)
· 浏览器原生「磁吸」效果!Anchor Positioning 锚点定位神器解析
· 没有源码,如何修改代码逻辑?
· 全程不用写代码,我用AI程序员写了一个飞机大战
· DeepSeek 开源周回顾「GitHub 热点速览」
· MongoDB 8.0这个新功能碉堡了,比商业数据库还牛
· 记一次.NET内存居高不下排查解决与启示
· 白话解读 Dapr 1.15:你的「微服务管家」又秀新绝活了
2017-12-28 sql joins
2016-12-28 LayoutControl
2015-12-28 git使用ssh协议,生成公钥和私钥,并指定私钥
2015-12-28 在cmd中登录ftp服务器