人工智能-机器学习-支持向量机SVM

一、scikit-learn 中的SVM

1、导入模块

# 导入模块
import numpy as np
import matplotlib.pyplot as plt

2、导入鸢尾花数据集

#导入鸢尾花数据集，并只取其中的两个类别及两个特征值
from sklearn import datasets
iris = datasets.load_iris()
X = iris.data
y = iris.target
X = X[y<2,:2]
y = y[y<2]
print(X,y)
print(X.shape,y.shape)

image-20240516224742530

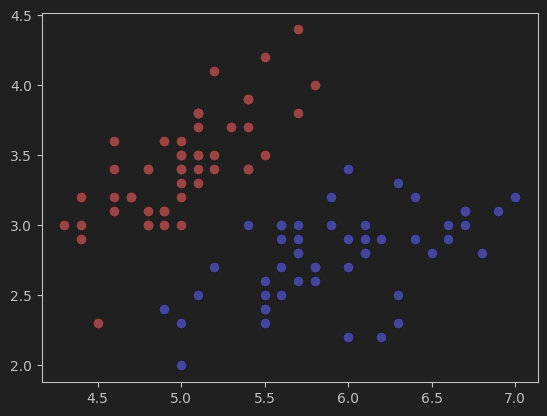
3、可视化数据集

#可视化数据集
plt.scatter(X[y==0,0],X[y==0,1],color='red')    # y==0,标签为0的数据
plt.scatter(X[y==1,0],X[y==1,1],color='blue')
plt.show()

image-20240516225057686

4、标准化数据集

# 标准化数据集
from  sklearn.preprocessing import StandardScaler
standardScaler = StandardScaler()
standardScaler.fit(X)
X_standard = standardScaler.transform(X)    # X_standard为标准化后的数据

5、定义绘制决策边界的函数

# 曲线勾画模型的决策边界函数
def plot_decision_boundary(model, axis):
    # 创建网格
    x0, x1 = np.meshgrid(
        np.linspace(axis[0], axis[1], int((axis[1] - axis[0]) * 100)).reshape(-1, 1),
        np.linspace(axis[2], axis[3], int((axis[3] - axis[2]) * 100)).reshape(-1, 1),
    )
    x_new = np.c_[x0.ravel(), x1.ravel()]
	# 预测
    y_predict = model.predict(x_new)
    zz = y_predict.reshape(x0.shape)
    # 引入自定义颜色映射
    from matplotlib.colors import ListedColormap
    custom_cmap = ListedColormap(['#EF9A9A','#FFF59D','#90CAF9'])
    # 绘制决策边界
    plt.contourf(x0, x1, zz, cmap=custom_cmap)

image-20240516225508240

6、实现硬间隔的SVM模型

# 导入硬间隔SVM，并训练模型
from sklearn.svm import LinearSVC
svc = LinearSVC(C=1e9)  # C=1e9表示正无穷大，C为错误样本的惩罚参数
svc.fit(X_standard,y)

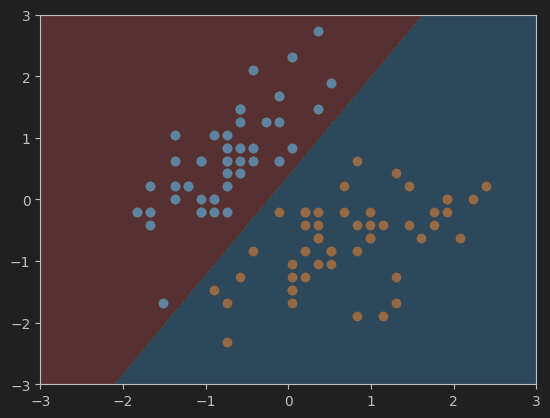
7、绘制硬间隔SVM决策边界

#画决策边界
plot_decision_boundary(svc, axis=[-3, 3, -3, 3])    # 横纵坐范围都为-3到3
plt.scatter(X_standard[y==0,0],X_standard[y==0,1])
plt.scatter(X_standard[y==1,0],X_standard[y==1,1])
plt.show()

image-20240516225814884

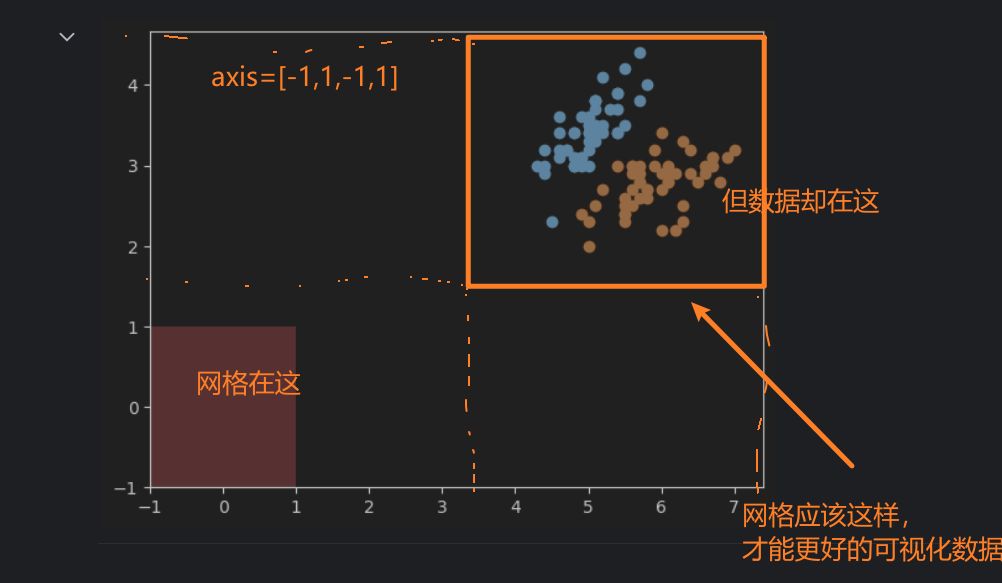
网格的大小应该如何设置？

image-20240516230124096

8、实现软间隔的SVM模型

#实现软间隔的SVM模型
svc2 = LinearSVC(C=0.01)
svc2.fit(X_standard,y)

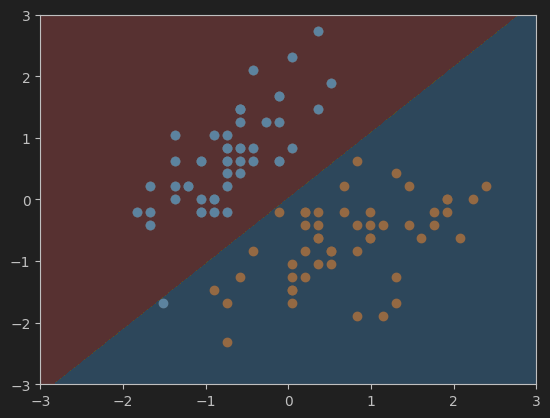
9、绘制软间隔的SVM决策边界

#可视化模型svc2的决策边界
plot_decision_boundary(svc2, axis=[-3, 3, -3, 3])   # model参数为svc2
plt.scatter(X_standard[y==0,0],X_standard[y==0,1])
plt.scatter(X_standard[y==1,0],X_standard[y==1,1])
plt.show()

image-20240516230224934

10、获取系数和截距

#获取系数和截距
print(svc2.coef_)
print(svc2.intercept_)

[[ 0.43789749 -0.410919  ]]
[0.00592601]

11、定义绘制决策边界、超平面的函数

#勾画决策边界以及支持向量机超平面函数
def plot_svc_decision_boundary(model, axis):
    # 决策边界（与上面的类似）
    x0, x1 = np.meshgrid(
        np.linspace(axis[0], axis[1], int((axis[1] - axis[0]) * 100)).reshape(-1, 1),
        np.linspace(axis[2], axis[3], int((axis[3] - axis[2]) * 100)).reshape(-1, 1),
    )
    x_new = np.c_[x0.ravel(), x1.ravel()]
    
    y_predict = model.predict(x_new)
    zz = y_predict.reshape(x0.shape)
    
    from matplotlib.colors import ListedColormap
    custom_cmap = ListedColormap(['#EF9A9A','#FFF59D','#90CAF9'])
    
    plt.contourf(x0, x1, zz, cmap=custom_cmap)
    
    # 超平面
    w = model.coef_[0]
    b = model.intercept_[0]
    
    # 超平面的方程是 w0*x0 + w1*x1 + b = 0，其中 w0 和 w1 是权重，x0 和 x1 是特征变量，b 是截距。
    # 以特征变量x1作为另一个特征变量x0的函数(可以理解为x0是自变量，x1是应变量)，来绘制平面==> x1 = -w0/w1 * x0 - b/w1
    plot_x = np.linspace(axis[0], axis[1], 200)
    
    # 计算超平面边界线、上下边界线，在x1轴上的值。(这里的x1轴类似于x-y坐标中的y轴,x0轴类似于x轴)
    y = -w[0]/w[1] * plot_x - b/w[1]
    up_y = -w[0]/w[1] * plot_x - (b+1)/w[1]
    down_y = -w[0]/w[1] * plot_x - (b-1)/w[1]
    
    # 筛选出位于axis[2]和axis[3]范围内的y_index、up_index、down_index
    # 也就是处于网格范围内的数据，网格之外的就不显示了
    y_index = (y >= axis[2]) & (y <= axis[3])
    up_index = (up_y >= axis[2]) & (up_y <= axis[3])
    down_index = (down_y >= axis[2]) & (down_y <= axis[3])
    
    # 画出超平面、上下边界线
    plt.plot(plot_x[y_index],y[y_index], color='black')
    plt.plot(plot_x[up_index], up_y[up_index], color='black')
    plt.plot(plot_x[down_index], down_y[down_index], color='black')

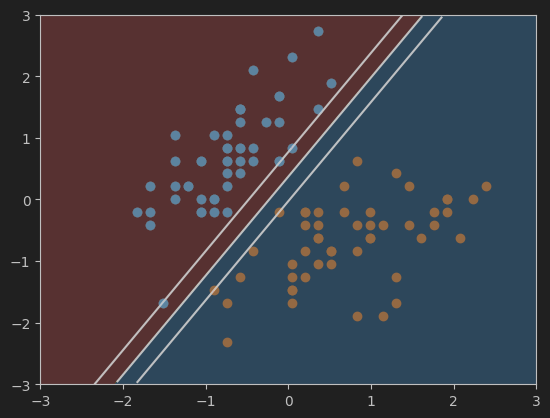
12、画软间隔SVM的超平面及决策边界

#画svc模型的超平面及决策边界
plot_svc_decision_boundary(svc, axis=[-3, 3, -3, 3])
plt.scatter(X_standard[y==0,0],X_standard[y==0,1])
plt.scatter(X_standard[y==1,0],X_standard[y==1,1])
plt.show()

image-20240516230717690

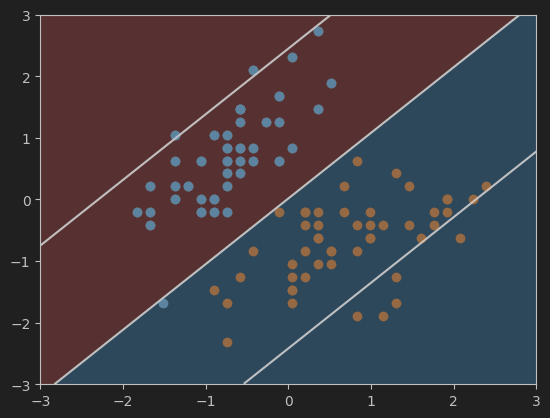
13、画硬间隔SVM的超平面及决策边界

#画svc2模型的超平面及决策边界
plot_svc_decision_boundary(svc2, axis=[-3, 3, -3, 3])
plt.scatter(X_standard[y==0,0],X_standard[y==0,1])
plt.scatter(X_standard[y==1,0],X_standard[y==1,1])
plt.show()

image-20240516230732085

二、SVM中使用多项式特征

1、导入make_moons数据集

#导入make_moons数据集
import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets

X, y = datasets.make_moons()    # 特征矩阵X和标签向量y
print(X.shape,y.shape)
print(X,y)

数据集形状和鸢尾花的差不多

image-20240516230914000

2、可视化数据集

#可视化导入的数据集
plt.scatter(X[y==0,0],X[y==0,1])
plt.scatter(X[y==1,0],X[y==1,1])
plt.show()

image-20240516230928318

3、重新导入打乱后的make_moons数据集并可视化

# 重新导入打乱后的make_moons数据集并可视化
X, y = datasets.make_moons(noise=0.15, random_state=666)

plt.scatter(X[y==0,0],X[y==0,1])
plt.scatter(X[y==1,0],X[y==1,1])
plt.show()

image-20240516231004037

4、使用Pipeline封装，并添加多项式特征

#使用Pipeline封装，并用PolynomialFeatures添加多项式特征
from sklearn.preprocessing import PolynomialFeatures,StandardScaler
from sklearn.svm import LinearSVC
from sklearn.pipeline import Pipeline

def PolynomialSVC(degree, C=1.0):
    # 使用Pipeline封装（简化了从原始特征到最终分类预测的整个流程）
    return Pipeline([
        ('poly', PolynomialFeatures(degree=degree)),    # 添加多项式特征
        ('std_scaler', StandardScaler()),   # 标准化数据
        ('linearSVC', LinearSVC(C=C))   # 使用线性支持向量机linearSVC进行分类
    ])

5、训练模型

#喂数据并训练模型
poly_svc = PolynomialSVC(degree=3)
poly_svc.fit(X,y)

6、定义绘制决策边界的函数

# 画模型的决策边界
def plot_decision_boundary(model, axis):
    # 创建网格
    x0, x1 = np.meshgrid(
        np.linspace(axis[0], axis[1], int((axis[1] - axis[0]) * 100)).reshape(-1, 1),
        np.linspace(axis[2], axis[3], int((axis[3] - axis[2]) * 100)).reshape(-1, 1),
    )
    x_new = np.c_[x0.ravel(), x1.ravel()]   # 合并网格
    
    y_predict = model.predict(x_new)
    zz = y_predict.reshape(x0.shape)    # 重塑为与网格相同形状的数组
    
    from matplotlib.colors import ListedColormap
    custom_cmap = ListedColormap(['#EF9A9A','#FFF59D','#90CAF9'])
    
    plt.contourf(x0, x1, zz, cmap=custom_cmap)  # 以填充的方式显示决策边界

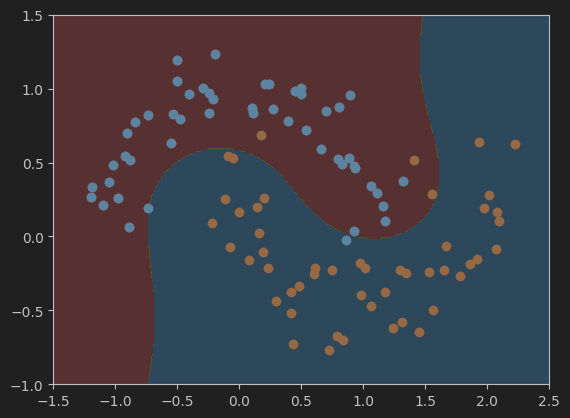
7、绘制决策边界

# 调用函数绘制决策边界
plot_decision_boundary(poly_svc, axis=[-1.5, 2.5, -1.0, 1.5])
# 画出数据集散点图
plt.scatter(X[y==0,0],X[y==0,1])
plt.scatter(X[y==1,0],X[y==1,1])
plt.show()

image-20240516231113714

8、使用多项式核函数的SVM

(1)、封装模型并训练

# 使用多项式核函数poly（并喂数据训练模型）
from sklearn.svm import SVC

# 定义封装模型
def PolynomialKernelSVC(degree, C=1.0):
    return Pipeline([
        ('sed_scaler', StandardScaler()),   # 标准化数据
        ('kernelSVC', SVC(kernel='poly', degree=degree, C=C))   # 使用多项式核函数poly
    ])

# 训练模型
poly_kernel_svc = PolynomialKernelSVC(degree=3)     # degree表示多项式的阶数
poly_kernel_svc.fit(X,y)

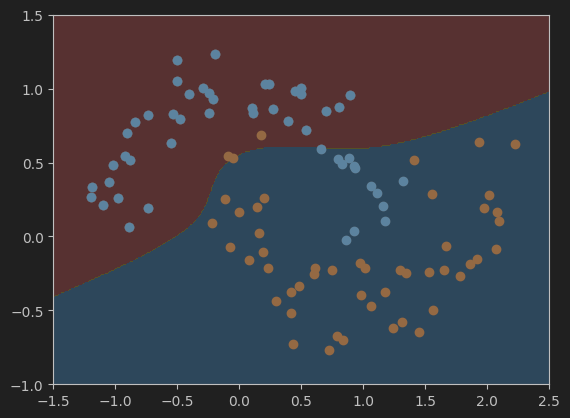
(2)、绘制模型决策边界

#可视化模型结果
# 绘制决策边界的函数plot_decision_boundary，在掐面膜已经定义过了，所以这里直接调用即可
plot_decision_boundary(poly_kernel_svc, axis=[-1.5, 2.5, -1.0, 1.5])
plt.scatter(X[y==0,0],X[y==0,1])
plt.scatter(X[y==1,0],X[y==1,1])
plt.show()

image-20240516231150749

三、直观理解高斯核函数

1、可视化一维数据

#可视化一维数据
import numpy as np
import matplotlib.pyplot as plt

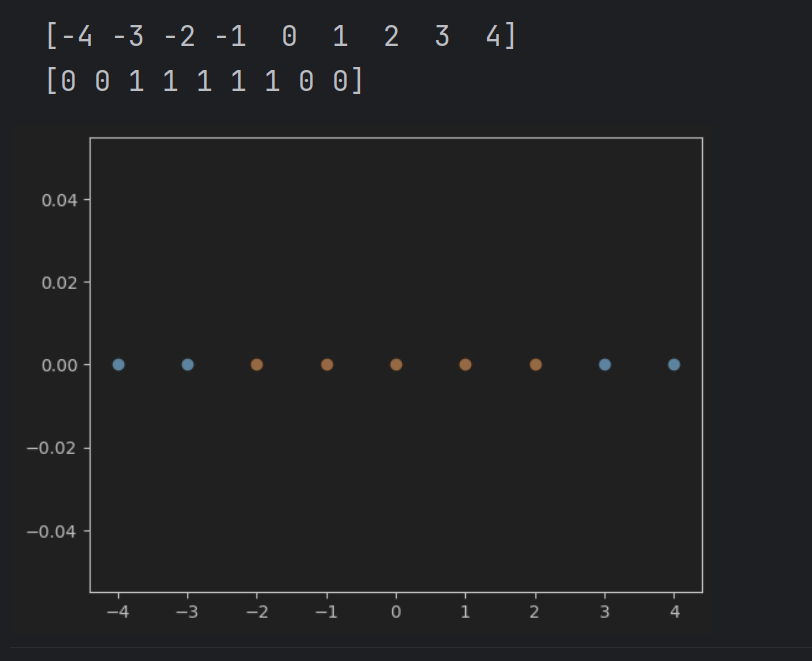
x = np.arange(-4,5,1)   # 与rnage类似
print(x)

y = np.array((x>=-2) & (x<=2), dtype = 'int')   # 在标签向量y中，标签向量值为1的元素表示对应的x值在-2到2之间
print(y)

# 画出数据集散点图
plt.scatter(x[y==0],[0]*len(x[y==0]))
# [0]*len(x[y==0])表示对应的y值都为0
plt.scatter(x[y==1],[0]*len(x[y==1]))
plt.show()

image-20240516231310295

2、可视化高斯函数升维后的结果

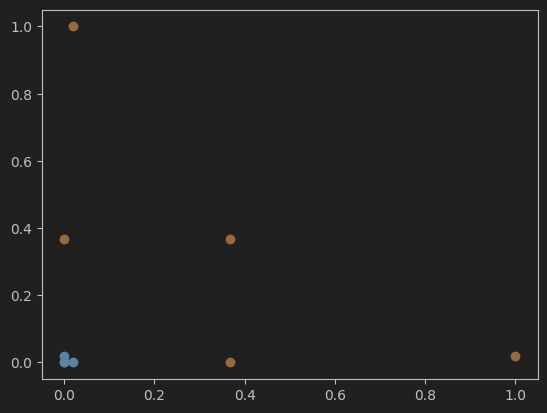
# 可视化使用高斯函数进行升维后的结果
def gaussian(x,l): 
    gamma = 1.0
    return np.exp(-gamma * ((x-l)**2))  # x与l之间距离的指数衰减值


l1, l2 = -1,1   # 高斯函数中心点

X_new = np.empty((len(x),2))
for i,data in enumerate(x):
    # 分别计算以l1和l2为中点，以l1和l2为中心的高斯值。
    X_new[i,0] = gaussian(data,l1)
    X_new[i,1] = gaussian(data,l2)

# 绘制高斯升维后的散点图
plt.scatter(X_new[y==0,0],X_new[y==0,1])
plt.scatter(X_new[y==1,0],X_new[y==1,1])
plt.show()

image-20240516231326120

四、scikit-learn 中的 RBF 核

1、加载并可视化make_moons数据集

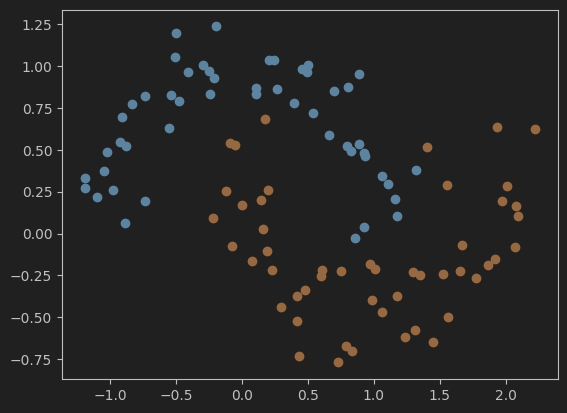
#加载并可视化make_moons数据集
import numpy as np
import matplotlib.pyplot as plt

from sklearn import datasets

X, y = datasets.make_moons(noise=0.15, random_state=666)
plt.scatter(X[y==0,0],X[y==0,1])
plt.scatter(X[y==1,0],X[y==1,1])
plt.show()

image-20240516231354425

2、使用RBF核函数的SVM训练模型

#使用带有高斯核函数（RBF）的SVM
from sklearn.preprocessing import StandardScaler
from sklearn.pipeline import Pipeline
from sklearn.svm import SVC

def RBFKernelSVC(gamma):
    return Pipeline([
        ('std_scaler', StandardScaler()),
        ('svc', SVC(kernel='rbf', gamma=gamma)) # 使用高斯核函数rbf
    ])

svc = RBFKernelSVC(gamma=1) # 建立模型
svc.fit(X,y)    # 训练模型

3、定义绘制决策边界的函数

#画决策边界的函数
def plot_decision_boundary(model, axis):
    
    x0, x1 = np.meshgrid(
        np.linspace(axis[0], axis[1], int((axis[1] - axis[0]) * 100)).reshape(-1, 1),
        np.linspace(axis[2], axis[3], int((axis[3] - axis[2]) * 100)).reshape(-1, 1),
    )
    x_new = np.c_[x0.ravel(), x1.ravel()]
    
    y_predict = model.predict(x_new)
    zz = y_predict.reshape(x0.shape)
    
    from matplotlib.colors import ListedColormap
    custom_cmap = ListedColormap(['#EF9A9A','#FFF59D','#90CAF9'])
    
    plt.contourf(x0, x1, zz, cmap=custom_cmap)

4、可视化决策边界

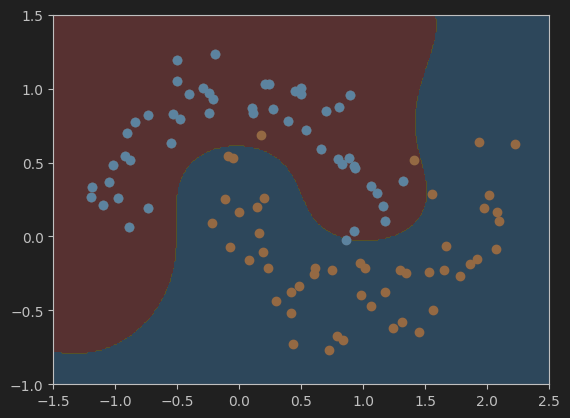
#可视化模型svc的决策边界
plot_decision_boundary(svc, axis=[-1.5, 2.5, -1.0, 1.5])
plt.scatter(X[y==0,0],X[y==0,1])
plt.scatter(X[y==1,0],X[y==1,1])
plt.show()

image-20240516231435044

5、分别绘制gamma值为100、10、0.5、0.1是的决策边界

#设置gamma值为100，并可视化模型的决策边界
svc_gamma100 = RBFKernelSVC(gamma=100)
svc_gamma100.fit(X,y)

plot_decision_boundary(svc_gamma100, axis=[-1.5, 2.5, -1.0, 1.5])
plt.scatter(X[y==0,0],X[y==0,1])
plt.scatter(X[y==1,0],X[y==1,1])
plt.show()

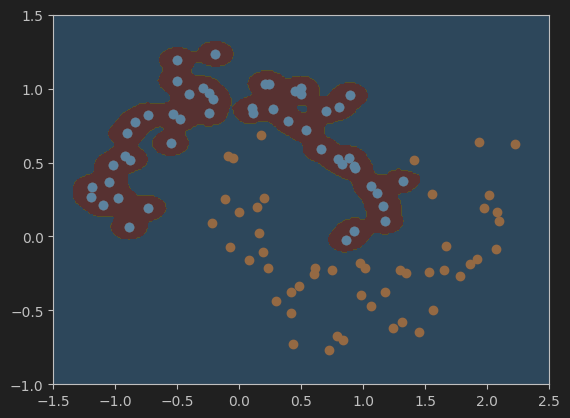
image-20240516231452640

#设置gamma值为10，并可视化模型的决策边界
svc_gamma10 = RBFKernelSVC(gamma=10)
svc_gamma10.fit(X,y)

plot_decision_boundary(svc_gamma10, axis=[-1.5, 2.5, -1.0, 1.5])
plt.scatter(X[y==0,0],X[y==0,1])
plt.scatter(X[y==1,0],X[y==1,1])
plt.show()

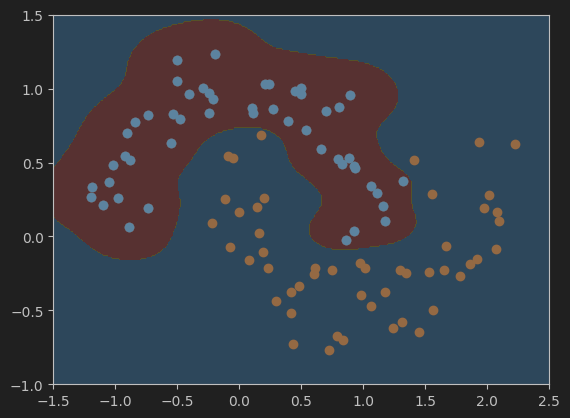
image-20240516231504864

#设置gamma值为0.5，并可视化模型的决策边界
svc_gamma05 = RBFKernelSVC(gamma=0.5)
svc_gamma05.fit(X,y)

plot_decision_boundary(svc_gamma05, axis=[-1.5, 2.5, -1.0, 1.5])
plt.scatter(X[y==0,0],X[y==0,1])
plt.scatter(X[y==1,0],X[y==1,1])
plt.show()

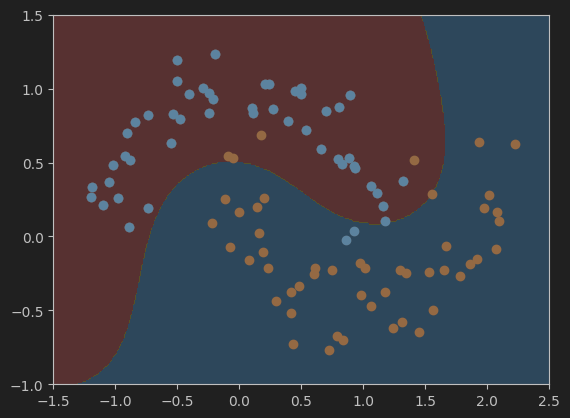
image-20240516231552318

#设置gamma值为0.1，并可视化模型的决策边界
svc_gamma01 = RBFKernelSVC(gamma=0.1)
svc_gamma01.fit(X,y)

plot_decision_boundary(svc_gamma01, axis=[-1.5, 2.5, -1.0, 1.5])
plt.scatter(X[y==0,0],X[y==0,1])
plt.scatter(X[y==1,0],X[y==1,1])
plt.show()

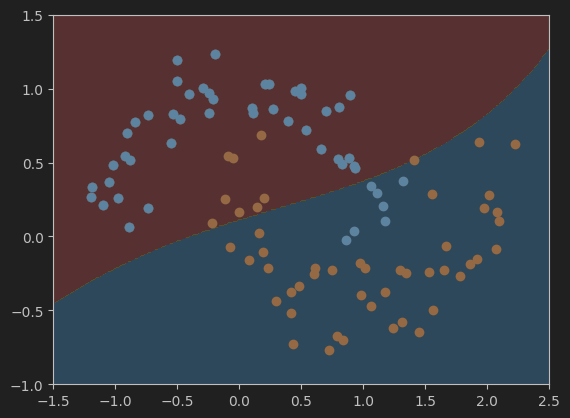
image-20240516231533301

总结

总的来说，不同gamma值会对模型的结果有一定的影响，所以在训练机器学习模型过程中超参数的选择也是一个比较重要的学习内容。

五、作业：

使用带有RBF核函数的SVM实现鸢尾花数据集的分类。
（1）导入鸢尾花数据集并可视化数据分布。
（2）导入模型。
（3）喂数据，训练模型。
（4）可视化模型决策边界。
（5）利用Accuracy评估模型效果。

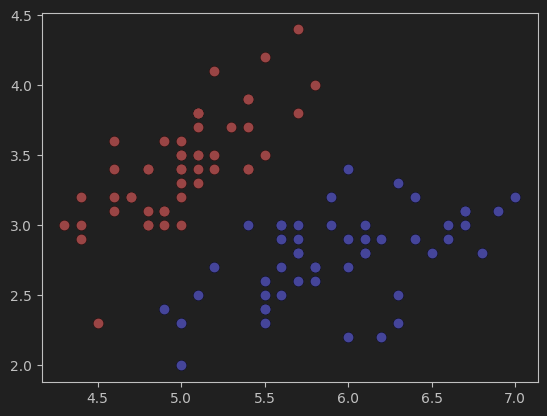
1、导入鸢尾花数据集并可视化数据分布

#导入鸢尾花数据集，并只取其中的两个类别及两个特征值
from sklearn import datasets
iris = datasets.load_iris()
X = iris.data
y = iris.target
X = X[y<2,:2]
y = y[y<2]

#可视化数据集
plt.scatter(X[y==0,0],X[y==0,1],color='red')    # y==0,标签为0的数据
plt.scatter(X[y==1,0],X[y==1,1],color='blue')
plt.show()

image-20240516231646939

2、创建并训练模型

#使用带有高斯核函数（RBF）的SVM
from sklearn.preprocessing import StandardScaler
from sklearn.pipeline import Pipeline
from sklearn.svm import SVC

def RBFKernelSVC(gamma):
    return Pipeline([
        ('std_scaler', StandardScaler()),   # 标准化
        ('svc', SVC(kernel='rbf', gamma=gamma)) # 使用高斯核函数rbf
    ])

svc = RBFKernelSVC(gamma=0.05) # 建立模型
# 一个个试，发现gamma=0.05效果最好(C默认为1)
# gamma=0.05效果就很好了，下面的网格搜搜索就不用了。
svc.fit(X,y)    # 训练模型

2.1、通过网格寻找合适的gamma值（可以不用）

# 通过网格寻找合适的gamma值
# 注意：这里说的网格和上面绘制决策边界时的网格不是一个意思。这里的网格应该说的是一种寻找最佳gamma和C值的方法。
from sklearn.model_selection import GridSearchCV

pipe = Pipeline([
    ('scaler', StandardScaler()),  # 首先对数据进行标准化
    ('svm', SVC(kernel='rbf'))  # 使用RBF核的SVM
])

# 一次次调整参数网格，找到最佳参数
param_grid = {'svm__gamma': [0.01, 0.1, 1, 10], 'svm__C': [0.1, 1, 10, 100]}  # 定义参数网格

grid_search = GridSearchCV(pipe, param_grid, cv=5)  # 使用5折交叉验证
grid_search.fit(X, y)  # 训练模型并找到最佳参数

best_gamma = grid_search.best_params_['svm__gamma']  # 获取最佳gamma值
best_C = grid_search.best_params_['svm__C']  # 获取最佳C值
print("Best gamma:", best_gamma)
print("Best C:", best_C)
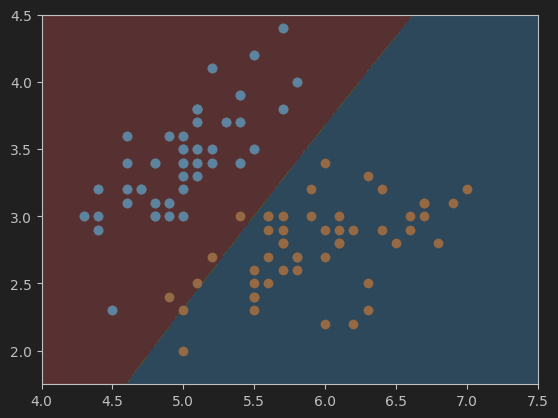
# 根据上面的网格搜索，得到的最佳参数如下。（效果不太好，准确度只有0.96）继续缩小范围，在0.1附近找。
# Best gamma: 0.1
# Best C: 0.1

# 训练模型
svc = SVC(kernel='rbf', gamma=best_gamma, C=best_C)
svc.fit(X, y)

这是gamma=0.1，Best C=0.1时的决策边界，准确度只有0.96。

image-20240516231821844

3、定义绘制决策边界的函数

#画决策边界的函数
def plot_decision_boundary(model, axis):
    
    x0, x1 = np.meshgrid(
        np.linspace(axis[0], axis[1], int((axis[1] - axis[0]) * 100)).reshape(-1, 1),
        np.linspace(axis[2], axis[3], int((axis[3] - axis[2]) * 100)).reshape(-1, 1),
    )
    x_new = np.c_[x0.ravel(), x1.ravel()]
    
    y_predict = model.predict(x_new)
    zz = y_predict.reshape(x0.shape)
    
    from matplotlib.colors import ListedColormap
    custom_cmap = ListedColormap(['#EF9A9A','#FFF59D','#90CAF9'])
    
    plt.contourf(x0, x1, zz, cmap=custom_cmap)

4、可视化决策边界

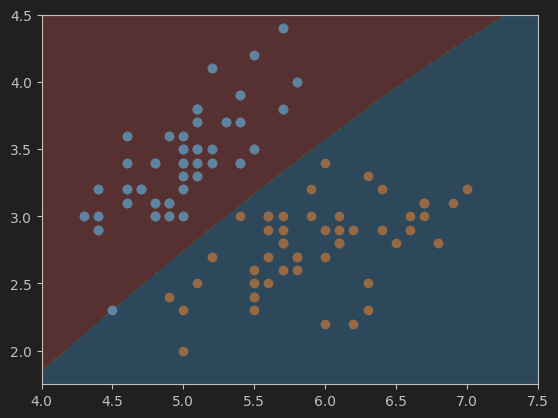
#可视化决策边界
plot_decision_boundary(svc, axis=[4.0, 7.5, 1.75, 4.5])	# 网格参数的选择（见下）
plt.scatter(X[y==0,0],X[y==0,1])
plt.scatter(X[y==1,0],X[y==1,1])
plt.show()

这是gamma=0.05，C=1时的决策边界，准确度为1.

image-20240516232254397

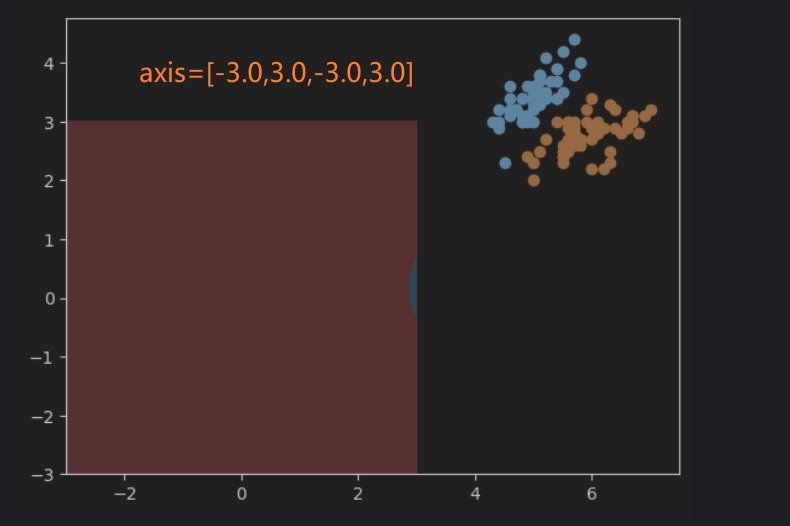
按照我的理解，网格的参数选取应该与数据在图中表示的范围有关。比如，鸢尾花原始的数据集在图中显示如下：

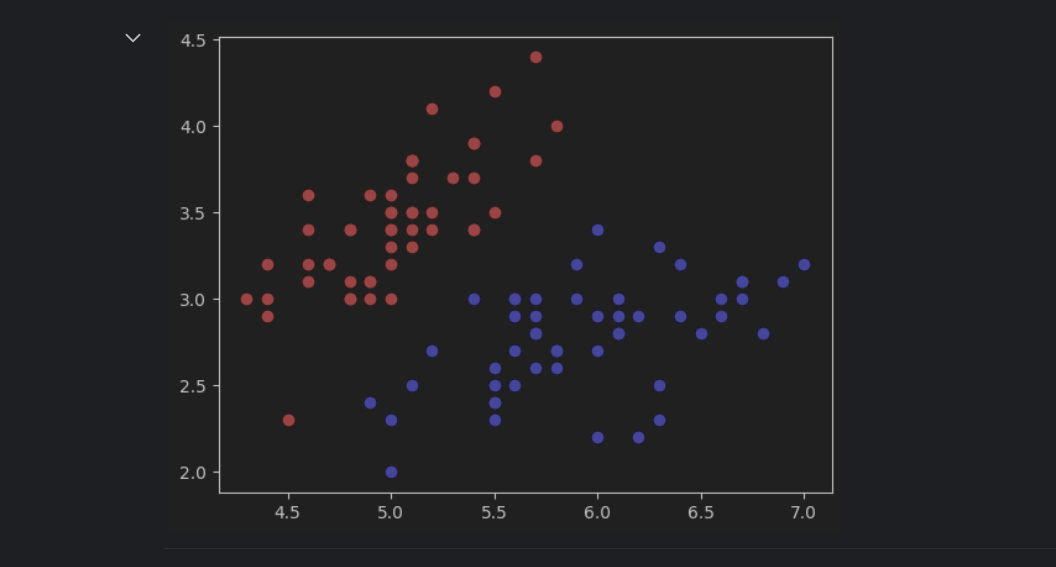
image-20240516232603934

x轴的范围大概在47.5之间，y轴的范围在1.54.5之间。根据这个范围来确定网格的参数，以保证网格能够正确的显示出数据。如果范围小了，可能会有一些数据显示不出来，大了的话，会导致数据在图像中太小，或者位置偏移中心，可视化效果不好。

image-20240516235518962

image-20240517000049264

5、使用Accuracy评估模型效果

# 使用Accuracy评估模型效果
from sklearn.metrics import accuracy_score
y_predict = svc.predict(X)
accuracy = accuracy_score(y, y_predict)
print('准确度：',accuracy)

写代码时问AI的一些记录，留作备份

鸢尾花数据集形状

image-20240516224742530

image-20240515202942213

image-20240515224719368

image-20240515225233017

image-20240515231547217

numpy数组

image-20240516103614832

SVM多项式

image-20240516105537775

直观理解高斯核函数

image-20240516112701638

gamma

image-20240516131015230

posted @ 2024-05-17 00:14  最爱喝开水  阅读(62)  评论(0)  编辑  收藏  举报