机器学习之聚类
公式实在不好敲呀,我拍了我笔记上的公式部分。原谅自己小学生的字体(太丑了)。
聚类属于无监督学习方法,典型的无监督学习方法还有密度估计和异常检测。
聚类任务:将数据集中的样本划分为若干个不相交的子集,每个子集为一个类。
性能指标(有效性指标):类内相似度高,类间相似度低。
性能度量:
(1)外部指标:
将性能结果C={Ci, i=1...k},与参考模型结果C*{C*i, i=1..s}进行对比(其中参考模型一般为专家根据经验划分的类),得出一些参数:

根据这些参数算出不同的外部指标,这些指标都在0-1之间,且值越大越好

(2)内部指标:(只考虑聚类结果,有距离来定义各个参数)

- 距离计算
距离性质:

常用距离(范数):
1、闵可夫斯基距离:

2、曼哈顿距离:
3、欧氏距离(最常用):
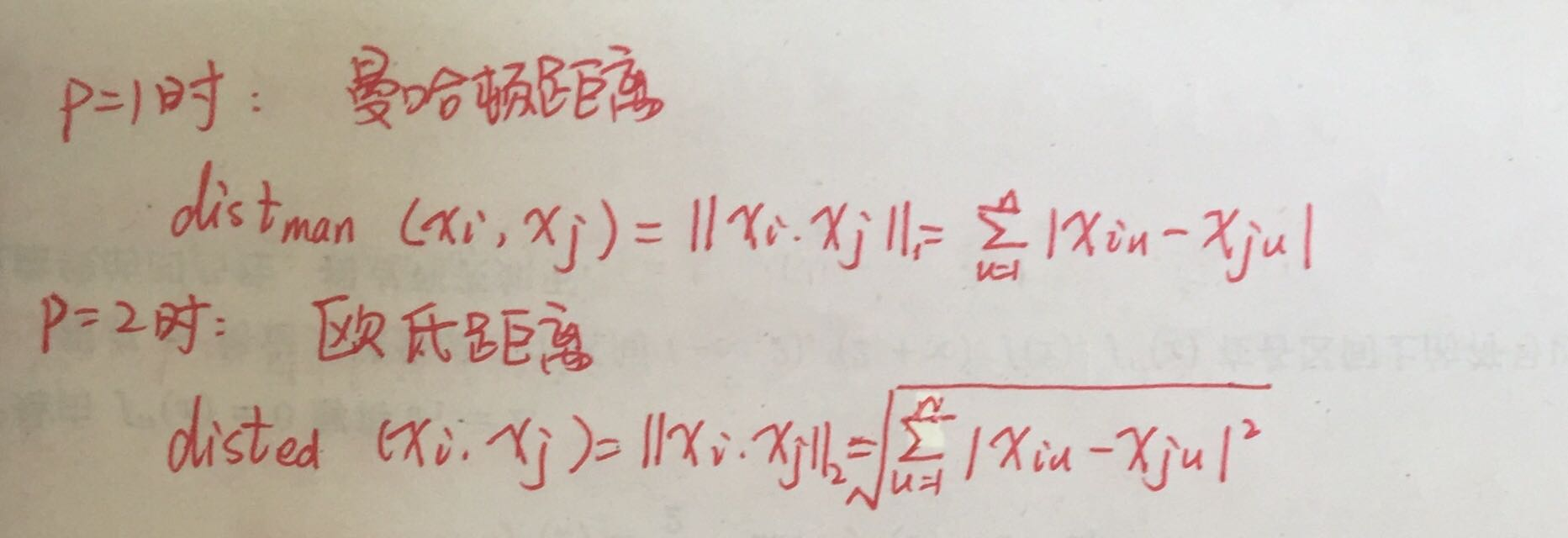
3、VDM距离

4、闵可夫与VDM结合(混合属性)
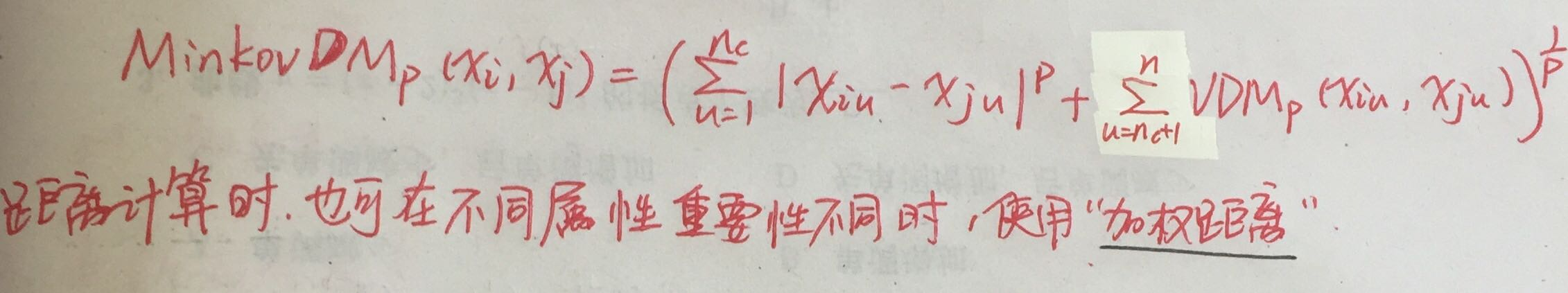
- 原型聚类
1、K-means(简单又经典的聚类方法):
input:样本集 D={xi, i=1...m},
k(欲分类类别个数)
output:划分为K类:C={Ci, i=1...k}
步骤:
(1)随机选取K个样本作为均值向量
(2)计算每个样本与各均值向量的距离
(3)由刚刚划分出的类别求出新的均值向量,再重复步骤(2)
(4)直到n+1轮迭代与第n轮相同(相似),算法停止迭代
2、学习向量量化(Learning Vector Quantization, LVQ)
思路:找一组原型你向量刻画聚类结构,但此算法假设数据样本都是带有类标记的。用样本本身的类标记进行辅助聚类。
input:样本集D={(xi,yi),i=1...m}
原型向量个数q,各原型向量预设类别标记{ti, i=1...q}
学习率:η
output:原型向量
步骤:
(1)初始化一组原型向量
(2)选取样本,找到与其最近的原型向量(以距离刻画)
(3)根据样本本身类标记与原型类标记是否一致决定如何更新原型向量。
(4)更新公式:
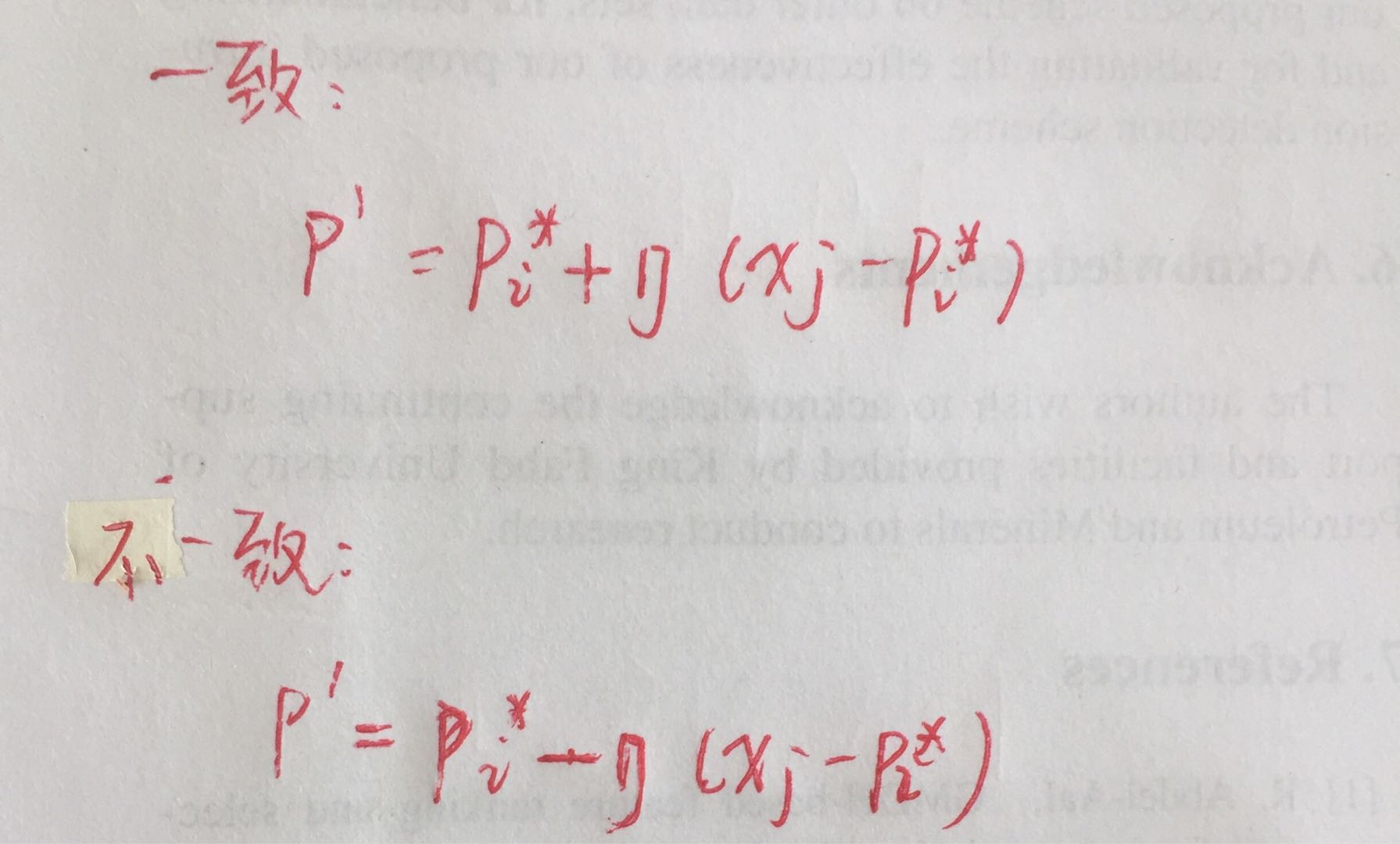
(5)满足条件(迭代次数或其他)后迭代停止。
3、高斯混合聚类
高斯分布(正态分布):
混合分布:



