机器学习之朴素贝叶斯&贝叶斯网络
- 贝叶斯决决策论
在所有相关概率都理想的情况下，贝叶斯决策论考虑基于这些概率和误判损失来选择最优标记，基本思想如下：
（1）已知先验概率和类条件概率密度（似然）
（2）利用贝叶斯转化为后验概率
（3）根据后验概率的大小进行决策分类
1、风险最小化
风险：根据后验概率可以获得将样本分为某类所产生的期望损失，即在该样本上的“条件风险”。
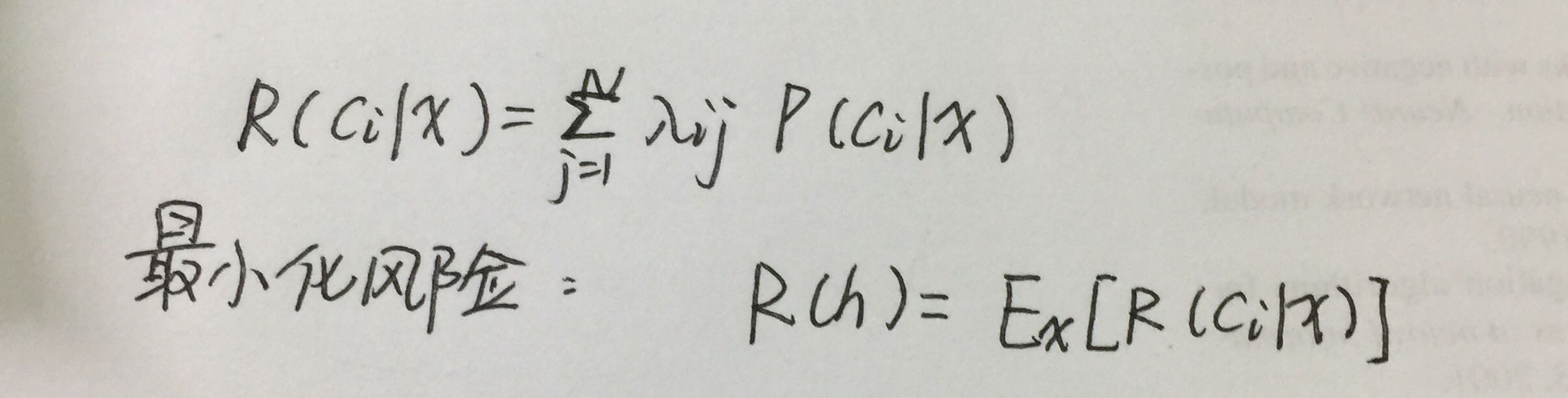
目的：寻找最小化总体风险，只需在每个样本上选择能使条件风险最小的类标记
2、决策风险最小化---后验概率最大化
获得后验概率有两种方法，机器学习也因为这两种方法被分为判别模型和生成模型。
判别模型：对于给定的x, 通过建模P(c|x)来预测c.
生成模型：先对联合分布P(c,x)建模，在算出P(c|x)
- 朴素贝叶斯（NB）
假设：属性之间需要相互独立
算法：
input： 训练集T={(xi,yi)|i=1...N}
output：实例x的分类
- 半朴素贝叶斯（SNB）
适当地考虑一些属性之间的相互依赖关系
问题变为：寻找被依赖的属性，即父属性。
SPODE：所有属性都依赖于同一属性，通过交叉验证的方法确定超父属性。
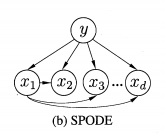
TAN（最大带权生成树）：
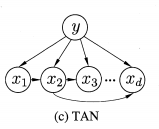
（1）计算量属性之间的互信息，作为两节点之间边的权重
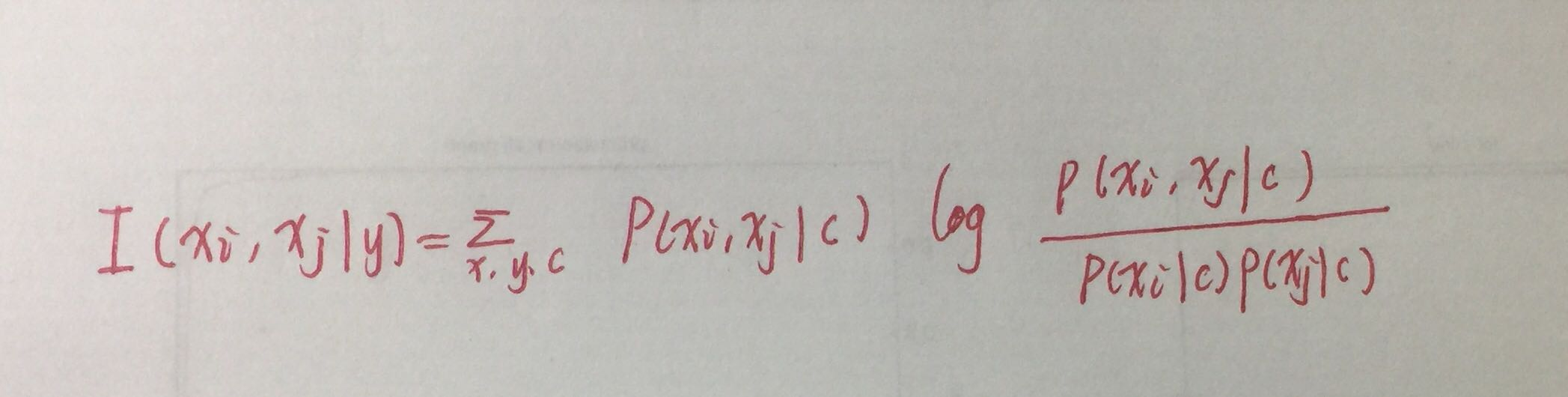
（2）插入最大权重边
（3）找到下一个最大边，并加入到树中，要求不成为环
（4）重复上述过程，直到插入n-1条边
（5）标出方向
AODE：
集成学习机制，更强大的独依赖分类器，尝试将每个属性作为超父来构建SPODE
- 贝叶斯网络（NB）
经典的概率图模型（有向无环图模型）
把某个研究系统中涉及的随机变量，根据能否条件独立的绘制在一张有向图中，就成了贝叶斯网络。一个贝叶斯网络由结构和参数两部分组成。
三个变量间的典型依赖关系：
（1）同父结构（tail-to-tail）
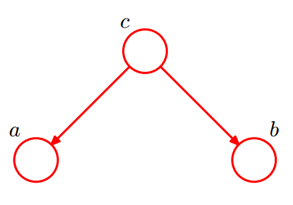
c已知的情况下，P(a,b,c)=P(a)P(b|c)P(b|c)，无法得出a,b独立。
c未知的情况下，a,b独立
（2）V型结构（head-to-head）
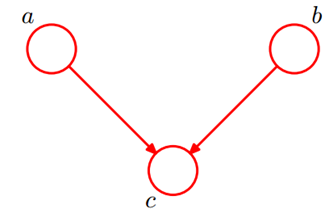c未知时，a,b独立
（3）顺序结构（head-to-tail）
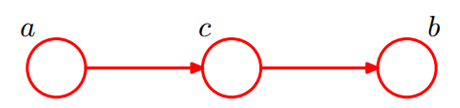
c已知时，a,b独立；反之，不独立。
- 如何学习构成一个贝叶斯网络
根据训练集学习出好的贝叶斯网络是解决问题的关键，“评分搜索”是常用的学习方法。
爬山算法：
（1）选择一个网络结构G（一般为空）
（2）计算这一结构的得分，并取最大得分
（3）随着得分的增大，循环进行：对边的增加和修正，更新最大得分
（4）返回一个有向图。
- R语言代码实现：
朴素贝叶斯：
贝叶斯网络：
