机器学习之决策树
小白我还记得前段时间问男神,分类决策树和回归决策树的区别是啥,现在回想起来,这个问题还真是很傻很无知呀。在粗去high之前又找了各种资料捋了一遍决策树的算法,为了不忘和更好的找到笔记,当然选择记录下来呀!啦啦啦!
一、决策树模型
决策树是一种基本的分类与回归方法,一般用于分类比较多。被认为是if-then规则的集合,也是在特征空间与类空间上的条件概率分布。
优点:可读性强(直观的展现变量之间的交互作用)
分类速度快(一般为二分类问题)
原则:损失函数最小化(一般用正则化的极大似然函数)
注:损失函数是用来度量预测错误的程度的,是预测值与真实值的非负实值函数,其值越小模型效果越好。
本质:从训练数据集中归纳出一种分类规则,从而与训练数据矛盾较小的树,同时具有较好的泛化能力。
决策树学习(训练)的三个步骤:(1)特征选择; (2)决策树的生成;(3)决策树的修剪。
发展历史:1986年Quinlan的ID3算法;1993年的C4.5算法,1984年Breiman的CART算法。
定义:一种描述对实例进行分类的树形结构,决策树由结点和有向边组成,结点分为两类:内结点与叶节点,内结点表示一个特种或属性,页节点表示一个类。
if-then规则:用于判断yes or no 。互斥并且完备的,即每一个实例都被有且仅有一条路径或一条规则所覆盖。
在特征空间与类空间上的条件概率分布:
设X为属性(特征),Y为类(类集合),条件分布P(Y|X),当P(Y=1|X=C)>0.5时,认为这个单元属于正类。
决策树学习算法三大要素:特征选择,决策树的生成,决策树的剪枝。
二、特征选择
准则:信息增益,信息增益比
1、信息增益:
- 熵(entroy,是随机变量的不确定性的度量)定义如下:

- 条件熵(conditional entropy)定义:
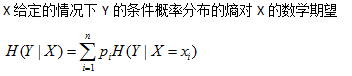
- 信息增益(information gain)定义:
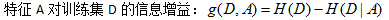
信息增益大的特征具有更强的分类能力。
- 信息增益算法:
input:训练集D和特征A
output:特征A对训练数据集D的信息增益g(D,A)
(1)计算数据集的经验熵H(D)
(2)计算特征A对数据集D的经验条件熵H(D|A)
(3)计算信息增益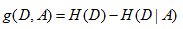
2、信息增益比:

三、决策树的生成
1、ID3算法
核心:在决策树的各个节点上应用信息增益准则选择特征,递归的构建决策树,相当于用极大似然法进行概率模型的选择。
缺点:该算法只有数的生成,故可能会产生过拟合现象
算法:
input:训练集D,特征集A,阈值ε
output:决策树T
(1)D中所有实例属于同一类,则T为单结点树,return T
(2)A=Φ,T为单结点树,return T
(3)否则,按照信息增益算法计算A中各特征对D的信息增益,选择信息增益最大的特征
(4)如果该信息的特征增益小于阈值ε,则T为单结点树,将训练集中实例数最大的类作为该节点的类标记,return T
(5)否则,对该特征的每一个可能值将训练集分为若干个子集,将子集中实例数最大的类作为标记,构建子结点,由结点和子结点构成数T,return T
(6)对每一个子节点,以自己作为训练集,以其余特征作为特征集,递归的调用前五步,生成树T,return T.
2、C4.5算法
这个算法是在ID3算法的基础上进行了改进,在C4.5生成决策树的过程中,用信息增益比来选择特征。
未完待续.........
笨宝宝要回去收拾行李出去玩了,回来再补全后面的CART算法和剪枝的内容吧!happy vacation!
浪了两个星期,根本不想学习,哈哈哈。
三、剪枝算法
决策树的剪枝一般是通过极小化决策树整体的损失函数或代价函数来实现的。
树的剪枝算法如下:
input:生成算法产生的整个树T, 参数α
output:修剪后的子树
(1)计算每个节点的经验熵
(2)递归的从树的叶节点向上回缩:如果子树的损失函数小,,则进行剪枝,即将父节点变为新的叶节点
(3)重复上述过程,直至不能继续为止,得到损失函数最小的子树
四、CART算法
此算法同样有特征选择、树的生成和剪枝组成,既可以用于分类树也可以用于回归树。其算法包括两部分:决策树的生成、剪枝
4.1、回归树的生成(最小二成回归法)
input:训练数据集D
output:回归树f(x)
(1)选择最优切分变量j与切分点s,求解:
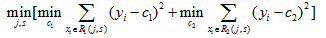
选择使上式达到最小值的(j,s)
(2)用选定的(j,s)划分区域并决定相应输出值
(3)继续对连个字区间调用(1)(2)直至满足条件
(4)将输入空间划分为M个区域,生成决策树
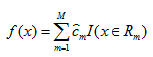
4.2、分类树的生成:
采用基尼指数选择最优特征,基尼指数值越大,样本集合的不确定性也就越大.
五、CART剪枝
由决策树的底端开始不断剪枝,直到根节点形成一个子树序列,然后通过交叉验证法在独立的验证数据集上对子数列进行测试,从中选择一个最优子树。



