离群值检测
离群值检测
离群值
outlier:样本中的一个或几个观测值,它们离其他观测值较远,暗示它们可能来自不同的总体。
离群值分类
- 总体固有变异性的极端表现,这类离群值与样本的其余观测值属于统一总体;
- 由于试验条件和试验方法的偶然偏离所产生的结果,或产生与观察、记录、计算中的失误,这类离群值与样本中其余观测值不属于统一总体。
数学小知识
方差:
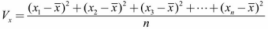
标准差:
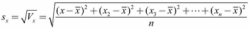
标准差能反映一个数据集的离散程度。
离群值检测方法
一、莱茵达准则(拉依达准则)
-
Z-score标准化辅助识别离群值,Z-score值表示原始样本x和样本均值μ之间的距离,而且这个距离以标准差σ为单位进行计算:Z-score(x)=(x-μ)/σ
-
得到样本的Z-score值后,通常将满足条件|Z-score(x)|>3的样本视为离群值(3σ法)。
![]()
-
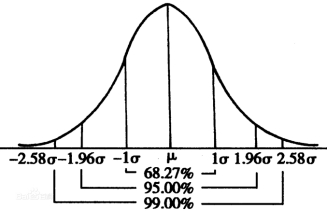
正态曲线下:
-
横轴区间(μ-σ,μ+σ)内的面积为68.268949%。
P{|X-μ|<σ}=2Φ(1)-1=0.6826
-
横轴区间(μ-1.96σ,μ+1.96σ)内的面积为95.449974%。
P{|X-μ|<2σ}=2Φ(2)-1=0.9544
-
横轴区间(μ-2.58σ,μ+2.58σ)内的面积为99.730020%。
P{|X-μ|<3σ}=2Φ(3)-1=0.9974
-
二、箱线图
-
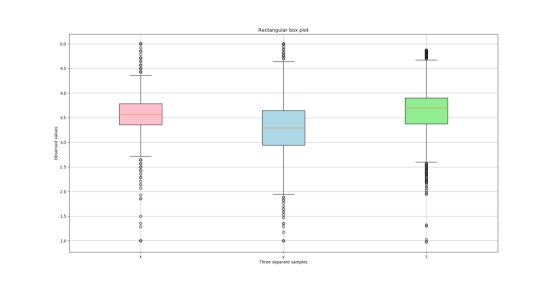
箱形图也叫箱线图,是检验样本数据中异常值的常用方法,与3σ法不同,箱形图法既可以用作服从正态分布样本数据异常值判断,也可以用作不服从正态分布样本数据异常值判断,适用范围广。
-
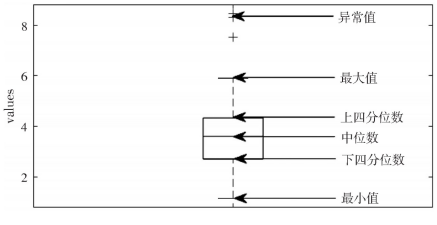
箱线图由最大值、上四分位数(Q3)、中位数(Q2)、下四分位数(Q1)和最小值五个统计量构成,Q1到Q3的间距为IQR,箱两端分别为上四分位数 (Q3)、下四分位数 (Q1) , 最大值、最小值分别为箱两端的须, 箱线图法中样本数据大于Q3+1.5IQR和小于Q-1.5IQR定义为异常值 (outlier) .箱线图结构下图所示.
![]()
-
Python做图示例
![]()
三、基于近邻判断离群值
-
对样本的离群程度进行量化,分数由它与K个最近邻的距离决定,分数的取值[0,+∞]:
- 计算每一个样本与其最近的K个近邻样本的距离,放到集合C中。
- 对C中的所有元素进行降序排列。
- 根据给定的距离阈值,选取C中大于给定阈值的距离所对应的样本作为离群值。
-
距离计算
-
欧氏距离
![]()
-
曼哈顿距离
![]()
-
欧式距离的缺点
-
欧式距离看起来非常合理,例如二维下的欧式距离就是勾股定理算距离,但是合理性这个需要在统一测量尺度的前提下,例如两个维度分别是{身高1700mm、体重0.060T},{身高1900mm、体重0.080T}这类数据肯定是身高特征对两点的距离影响大。但是两个维度特征是平等的,就因为测量尺度不统一,造成身高对两点的距离影响大,这就不合理了。
-
马氏距离:
表示数据的协方差距离。它是一种有效的计算两个未知样本集的相似度的方法。与欧氏距离不同的是,它考虑到各种特性之间的联系(例如:一条关于身高的信息会带来一条关于体重的信息,因为两者是有关联的),并且是尺度无关的(scale-invariant),即独立于测量尺度。
---以上总结参考于《数据科学导引》,国家标准GBT 4883-2008 数据的统计处理和解释 正态样本离群值的判断和处理



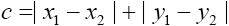


 浙公网安备 33010602011771号
浙公网安备 33010602011771号