动态规划(dynamic programming)
A - Coin Change[多重背包]
#include<stdio.h>
#include<string.h>
#include<iostream>
#include<algorithm>
const int MONEY= 251;
const int COIN = 101;
using namespace std;
int type[5]={1,5,10,25,50};
int dp[MONEY][COIN]={0};
void solve()
{
dp[0][0]=1;
for(int i=0;i<5;++i)
for(int j=1;j<COIN;++j)
for(int k = type[i] ; k < MONEY ; ++k)
dp[k][j]=dp[k][j] + dp[k - type[i]][j-1];
}
int main()
{
int s;
int ans[MONEY]={0};
solve();
for(int i=0;i<MONEY;++i)
for(int j=0;j<COIN;++j)
ans[i]+=dp[i][j];
while(cin>>s)
cout<<ans[s]<<endl;
return 0;
}
B - Bone Collector[01背包]
#include<stdio.h>
#include<string.h>
#include<iostream>
#include<algorithm>
#define MAX 1005
using namespace std;
struct a
{
int weight;
int value;
}bone[MAX];
int dp[MAX][MAX],T,N,V;
int main()
{
cin>>T;
while(T--)
{
cin>>N>>V;
memset(bone,0,sizeof(bone));
memset(dp,0,sizeof(dp));
for(int i=1;i<=N;++i) cin>>bone[i].value;
for(int i=1;i<=N;++i) cin>>bone[i].weight;
for(int i=1;i<=N;++i)
{
for(int j=V;j>=0;--j)
{
if(j>=bone[i].weight)
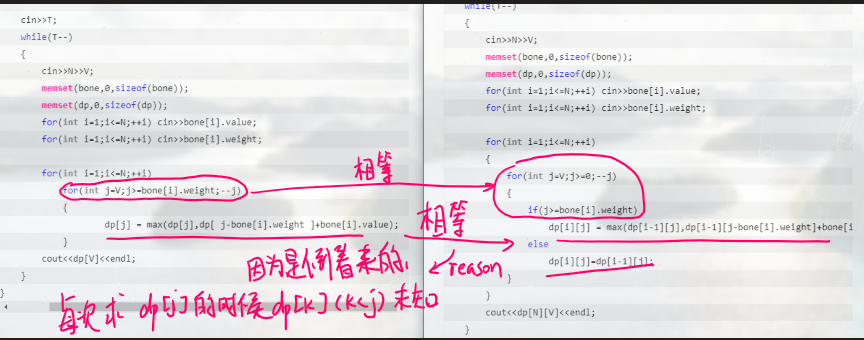
dp[i][j] = max(dp[i-1][j],dp[i-1][j-bone[i].weight]+bone[i].value);
else
dp[i][j]=dp[i-1][j];
}
}
cout<<dp[N][V]<<endl;
}
}
滚动数组二维化一维:
#include<stdio.h>
#include<string.h>
#include<iostream>
#include<algorithm>
#define MAX 1005
using namespace std;
struct a
{
int weight;
int value;
}bone[MAX];
int dp[MAX],T,N,V;
int main()
{
cin>>T;
while(T--)
{
cin>>N>>V;
memset(bone,0,sizeof(bone));
memset(dp,0,sizeof(dp));
for(int i=1;i<=N;++i) cin>>bone[i].value;
for(int i=1;i<=N;++i) cin>>bone[i].weight;
for(int i=1;i<=N;++i)
for(int j=V;j>=bone[i].weight;--j)
{
dp[j] = max(dp[j],dp[ j-bone[i].weight ]+bone[i].value);
}
cout<<dp[V]<<endl;
}
}
C - Common Subsequence
#include<stdio.h>
#include<string.h>
#include<string>
#include<iostream>
#include<algorithm>
#define MAX 1005
using namespace std;
int dp[1005][1005];
string str1,str2;
int LCS()
{
memset(dp,0,sizeof(dp));
for(int i=1;i<=str1.length();++i)
for(int j=1;j<=str2.length();++j)
{
if(str1[i-1]==str2[j-1]) dp[i][j]=dp[i-1][j-1]+1;
else dp[i][j] = max(dp[i-1][j],dp[i][j-1]);
}
return dp[str1.length()][str2.length()];
}
int main()
{
while(cin>>str1>>str2)
cout<<LCS()<<endl;
return 0;
}
Longest common subsequence问题:
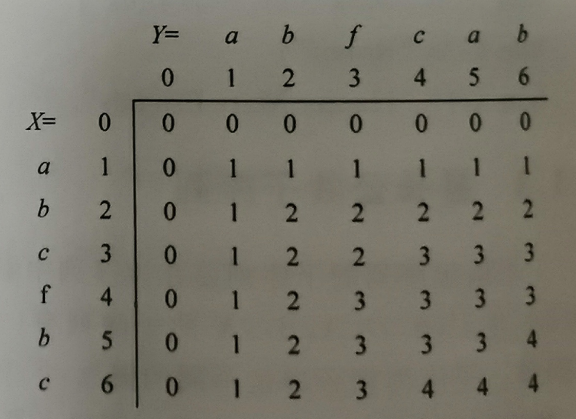
已知两序列,求这两个序列的最长公共子序列(不一定要连续)的长度。设二维数组dp[i][j]表示长度分别为i和j的序列A和B的LCS的最大长度,有状态转移方程:A[i]=B[j]时,dp[i][j]=dp[i-1][j-1]+1;A[i]≠B[j]时,dp[i][j]=max{dp[i-1][j],dp[i][j-1]}。
通过观察发现:
状态dp[i][j]只与当前行(dp[i][j-1])和上一行(dp[i-1][j],dp[i-1][j-1])的状态有关。这样,我们可以设置2个一维数组c1[],c2[],其中c1[]保存上一行的状态信息,c2[]更新当前行的状态信息,更新完毕之后再将c2[]的状态信息复制到c1[]中,循环结束后c1[length_B]就是所求LCS的最大长度,从而降低了空间需求。
滚动数组解法:
#include<stdio.h>
#include<string.h>
#include<string>
#include<iostream>
#include<algorithm>
#define MAX 1005
using namespace std;
int dp[1005][1005];
string str1,str2;
int LCS()
{
memset(dp,0,sizeof(dp));
for(int i=1;i<=str1.length();++i)
{
for(int j=1;j<=str2.length();++j)
{
if(str1[i-1]==str2[j-1])
dp[i%2][j]=dp[(i-1)%2][j-1]+1;
else
dp[i%2][j] = max(dp[(i-1)%2][j],dp[i%2][j-1]);
}
}
return dp[str1.length()%2][str2.length()];
}
int main()
{
while(cin>>str1>>str2)
cout<<LCS()<<endl;
return 0;
}
- 奇偶性——把行压缩成0,1,相邻两行的奇偶性一定是不同的,这样节省了复制的过程
- 相差1行-->奇偶性不同-->dp[i%2][j]=dp[(i-1)%2][j-1]+1
- 如果i为奇数:dp[i][j]在第1行,dpdp[(i-1)%2][j-1]在第0行
对于第一组数据,未使用滚动数组时dp的排列:
对第一组数据使用滚动数组时的排列:

D - 最少拦截系统[LCS]
#include<iostream>
#include<cstring>
#include<stdio.h>
#define MAX 10020
using namespace std;
int h[MAX];//导弹高度
int dp[MAX];//拦截系统
int main()
{
int n=0,v=0,m=0,pre=0;
while(~scanf("%d",&n))
{
for(int i=0;i<n;++i)
{
scanf("%d",&h[i]);
dp[i]=1;//每一个都可以被第一个拦截
}
for(int i=0;i<n;++i)
{
for(int j=0;j<i;++j)
{
if(h[i]>h[j]) dp[i]=max(dp[i],dp[j]+1);
}
}
m=0;
for(int i=0;i<n;++i) m=max(m,dp[i]);
cout<<m<<endl;
}
return 0;
}

G - 一只小蜜蜂...
wa了一次,到达50的时候用数据量超了int的范围,改成longlong就行了
#include<iostream>
#include
#include
#include
#define MAX 200
using namespace std;
long long dp[MAX];
int main()
{
int n=0,v=0,m=0;scanf("%d",&n);
for(int ii=0;ii<n;++ii)
{
scanf("%d%d",&m,&v);
memset(dp,0,sizeof(dp));
dp[m]=1,dp[m+1]=1;
for(int i=m+2;i<=v;++i)
{
dp[i]=dp[i-1]+dp[i-2];
}
cout<<dp[v]<<endl;
}
return 0;
}
F - 超级楼梯
#include<iostream>
#include<cstring>
#include<stdio.h>
#define MAX 200
using namespace std;
int dp[MAX];
int main()
{
int n,m;scanf("%d",&n);
for(int ii=0;ii<n;++ii)
{
scanf("%d",&m);
memset(dp,0,sizeof(dp));
dp[1]=1,dp[2]=1;
for(int i=3;i<=m;++i)
{
dp[i]=dp[i-1]+dp[i-2];
}
cout<<dp[m]<<endl;
}
return 0;
}
E - 母牛的故事
#include<iostream>
#include<cstring>
#include<stdio.h>
#define MAX 200
using namespace std;
int dp[MAX];
int main()
{
int n;
while(~scanf("%d",&n)&&(n!=0))
{
memset(dp,0,sizeof(dp));
dp[1]=1,dp[2]=2,dp[3]=3;
for(int i=4;i<=n;++i)
{
dp[i]=dp[i-1]+dp[i-3];
}
cout<<dp[n]<<endl;
}
return 0;
}
H - 折线分割平面
#include<stdio.h>
#include<string.h>
#include<string>
#include<iostream>
#include<algorithm>
#include<vector>
#define MAX 1005
using namespace std;
const int N=10000;
int dp[N];
int n,m;
int main()
{
cin>>n;
for(int i=0;i<n;++i)
{
cin>>m;
memset(dp,0,sizeof(dp));
for(int i=1;i<=m;++i)
{
dp[i] = dp[i-1]+(i-1)*4+1;
}
cout<<dp[m]+1<<endl;
}
return 0;
}

I - Frog[01背包?]
#include<stdio.h>
#include<string.h>
#include<string>
#include<iostream>
#include<algorithm>
#include<vector>
using namespace std;
const int MAX=205;
int dp[MAX][MAX],ins[MAX];
int N,n,A,B,K,res;
int main()
{
cin>>n;
for(int I=0;I<n;++I)
{
cin>>N>>A>>B>>K;
memset(dp,0,sizeof(dp));
memset(ins,0,sizeof(ins));
for(int ii =0;ii<N;++ii) cin>>ins[ii];
dp[0][0]=ins[0];
for(int i=1;i<N;++i)
{
for(int j=1;j<=K;++j)
{
for(int t=A;i>=t&&t<=B;++t)
{
dp[i][j] = max(dp[i][j],dp[i-t][j-1]+ins[i]);
res=max(res,dp[i][j]);
}
}
}
cout<<res<<endl;
}
return 0;
}

J - The King’s Ups and Downs[组合]
最烦组合了,欸蹭蹭很有道理,给别人讲也说有道理可就是不对,岂可休!
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
ll ans[25],dp[25][2],c[25][25];
void zuhe()
{
int i,j;
for (i=0;i<=20;i++)
c[i][0] = 1;
for (i=1;i<=20;i++)
for (j=1;j<=20;j++)
c[i][j] = c[i-1][j] + c[i-1][j-1];
}
void listt()
{
int k,i,j;
ans[1] = 1;
dp[0][0] = dp[0][1] = 1;
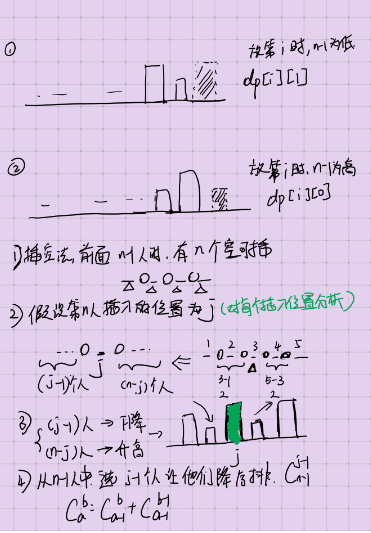
dp[1][0] = dp[1][1] = 1;//前面0个人,放前放后一种情况
for (k=2;k<=20;k++)
{
ll cnt = 0;
for (i=0;i<k;i++)
{
cnt += dp[i][0]*dp[k - i - 1][1]*c[k-1][i];
}
ans[k] = cnt;
dp[k][0] = dp[k][1] = cnt / 2;//对称分布
}
}
int main()
{
zuhe();//计算一下组合数
listt();
int t;
scanf("%d",&t);
while (t--)
{
ll cas,n;
scanf("%lld %lld",&cas,&n);
printf("%lld %lld\n",cas,ans[n]);
}
return 0;
}
#handwriting:
- 01背包从大到小枚举
- 完全背包从小到大枚举
- 二进制优化:(当要取的物品个数过多的时候,用二进制的形式来表示“取法”)把它的件数C 用分解成若干个件数,这里面数字可以组合成任意小于等于C的件数,而且不会重复,这样分解和二进制很相似,每个数都可以分解成2的多少次幂的和,把他们相加即可
- C=7,对每件物品有两种选择 “ 取or不取 ” (在状态转移方程中体现),7 可分解成 1 2 4 三个数字,则0-7的数都可以用1,2,4表示
- 选0个物品:;选1个物品:1;选 2个物品:2;选 3个物品:1+2 ;选4个物品:4;选5个物品:1+4;选6个物品:2+4;选7个物品:1+2+4
- C=10,10 可分解为1 2 4 3
- 选0个物品:;选1个物品:1;选 2个物品:2;选 3个物品:1+2 ;选4个物品:4;选5个物品:1+4;选6个物品:2+4;选7个物品:1+2+4;选8个物品:3+4+1;选9个物品:2+3+4;选10个物品:1+2+3+4
- 所以我们可以只对拆出来这组数逐一进行01背包,而不用从1到C都要01背包一次,就可以把O(c)的部分优化成O(logc)
-
 模板
模板#include<stdio.h> #include<string.h> #include<string> #include<iostream> #include<algorithm> #include<vector> #define MAX 1005 using namespace std; const int N=2010; int f[N]; int n,m; struct Good { int v,w; }; int main() { vector<Good>goods; cin>>n>>n; for(int i=0;i<n;++i) { int v,w,s; cin>>v>>w>>s; //对每件物品进行个数拆分 for(int k=1;k<=s;k*=2) { s-=k; goods.push_back({v*k,w*k}); } if(s>0) goods.push_back({v*s,w*s}); } //01背包 for(auto good:goods) for(int j=m;j>=good.v;j--) f[j] = max(f[j],f[j-good.v]+good.w); cout<<f[m]; return 0; }
- C=7,对每件物品有两种选择 “ 取or不取 ” (在状态转移方程中体现),7 可分解成 1 2 4 三个数字,则0-7的数都可以用1,2,4表示