第四周训练 | 并查集
A - How Many Tables
#include<iostream> using namespace std; const int maxn = 1050; int set[maxn]; void init_set() { for(int i=0;i<=maxn;++i)set[i]=i; } int find_set(int x) { return x==set[x]?x:find_set(set[x]); } void union_set(int x,int y) { x=find_set(x); y=find_set(y); if(x!=y)set[x]=set[y]; } int main() { int t,n,m,x,y; cin>>t; while(t--) { cin>>n>>m; init_set(); for(int i=1;i<=m;++i) { cin>>x>>y; union_set(x,y); } int ans=0; for(int i=1;i<=n;++i) { if(set[i]==i)ans++; } cout<<ans<<endl; } return 0; }
优化版,降低了树高:
#include<iostream> using namespace std; const int maxn = 1050; int set[maxn],height[maxn]; void init_set() { for(int i=0;i<=maxn;++i) { set[i]=i; height[i]=0; } } int find_set(int x) { return x==set[x]?x:find_set(set[x]); } void union_set(int x,int y) { x=find_set(x); y=find_set(y); if(height[x]==height[y]) { height[x]+=1; set[y]=x; } else { if(height[x]<height[y])set[x]=y; else set[y]=x; } } int main() { int t,n,m,x,y; cin>>t; while(t--) { cin>>n>>m; init_set(); for(int i=1;i<=m;++i) { cin>>x>>y; union_set(x,y); } int ans=0; for(int i=1;i<=n;++i) { if(set[i]==i)ans++; } cout<<ans<<endl; } return 0; }
路径压缩版本:
#include<iostream> using namespace std; const int maxn = 1050; int set[maxn],height[maxn]; void init_set() { for(int i=0;i<=maxn;++i) { set[i]=i; height[i]=0; } } int find_set(int x) { if(x!=set[x])set[x]=find_set(set[x]); return set[x]; } void union_set(int x,int y) { x=find_set(x); y=find_set(y); if(height[x]==height[y]) { height[x]+=1; set[y]=x; } else { if(height[x]<height[y])set[x]=y; else set[y]=x; } } int main() { int t,n,m,x,y; cin>>t; while(t--) { cin>>n>>m; init_set(); for(int i=1;i<=m;++i) { cin>>x>>y; union_set(x,y); } int ans=0; for(int i=1;i<=n;++i) { if(set[i]==i)ans++; } cout<<ans<<endl; } return 0; }
非递归写法:
#include<iostream> using namespace std; const int maxn = 1050; int set[maxn],height[maxn]; void init_set() { for(int i=0;i<=maxn;++i) { set[i]=i; height[i]=0; } } int find_set(int x) { int r=x; while(set[r]!=r)r=set[r]; int i=x,j; while(i!=r) { j=set[i];set[i]=r;i=j; } return set[x]; } void union_set(int x,int y) { x=find_set(x); y=find_set(y); if(height[x]==height[y]) { height[x]+=1; set[y]=x; } else { if(height[x]<height[y])set[x]=y; else set[y]=x; } } int main() { int t,n,m,x,y; cin>>t; while(t--) { cin>>n>>m; init_set(); for(int i=1;i<=m;++i) { cin>>x>>y; union_set(x,y); } int ans=0; for(int i=1;i<=n;++i) { if(set[i]==i)ans++; } cout<<ans<<endl; } return 0; }
B - Ubiquitous Religions
真·套板子
#include<iostream> #define MAX 50003 using namespace std; int n,m,i,j,index; int stu[MAX]; int height[MAX]; void intial() { for(int i=1;i<=n;++i) { stu[i]=i;height[i]=0; } } int find_father(int x) { int r=x; while(stu[r]!=r)r=stu[r]; int i=x,j; while(i!=r)//路径压缩 { j=stu[i];stu[i]=r;i=j; } return stu[x]; } void union_stu(int i,int j) { i=find_father(i); j=find_father(j); if(height[i]==height[j]) { height[i]+=1; stu[j]=i; } else { if(height[i]<height[j])stu[j]=i; else stu[i]=j; } } int main() { while(cin>>n>>m&&(n||m)) { intial(); index++; for(int a=0;a<m;++a) { cin>>i>>j; union_stu(i,j); } int ans=0; for(int i=1;i<=n;++i) { if(stu[i]==i)ans++; } cout<<"Case "<<index<<": "<<ans<<endl; } return 0; }
C - The Suspects
输入变一变的套板子
#include<iostream> #define MAX 30004 using namespace std; int n,m,k,j,index; int stu[MAX]; int height[MAX]; void intial() { for(int i=0;i<n;++i) { stu[i]=i;height[i]=0; } } int find_father(int x) { int r=x; while(stu[r]!=r)r=stu[r]; int i=x,j; while(i!=r)//路径压缩 { j=stu[i];stu[i]=r;i=j; } return stu[x]; } void union_stu(int i,int j) { i=find_father(i); j=find_father(j); if(height[i]==height[j]) { height[i]+=1; stu[j]=i; } else { if(height[i]<height[j])stu[j]=i; else stu[i]=j; } } int main() { while(cin>>n>>m&&(n||m)) { intial(); for(int b=0;b<m;++b) { cin>>k;//输入这个组的总人数 if(k>1) { //先输入一个,后面的都以它为父 int father=0;cin>>father; for(int a=1;a<k;++a) { cin>>j; union_stu(j,father); } } else { int father;cin>>father; // stu[father]=father; } } int ans=1; int tag=find_father(0); for(int i=1;i<n;++i) { // cout<<"stu["<<i<<"]="<<stu[i]<<endl; if(find_father(i)==tag)ans++; } cout<<ans<<endl; } return 0; }
D - Find them, Catch them(带权并查集|种类并查集)
一开始超时,用cin读入后来改成scanf又因为考虑不周wa了,最后只好在网上找大佬的代码,原来是带权并查集,太强了,这里贴一下:https://zhuanlan.zhihu.com/p/42496208
#include<iostream> #include<cstdio> #include<cstring> using namespace std; const int N=1e5+10; int t,n,m,f[N],w[N];//w代表了当前节点与其父节点的关系 int find(int x) { if(x==f[x]) return x; int temp=f[x];//存放一下x的父亲 f[x]=find(f[x]);//找到x的祖先 w[x]=(w[x]+w[temp]+1)%2;//跟新x和他祖先的关系 return f[x];//0代表当前节点与其父节点分属不同的团伙,1代表两者来自同一团体 } void join(int x,int y) { //这里有一个隐含关系x,y不是再一个组里 int fx=find(x),fy=find(y); if(fx!=fy) { f[fx]=fy;//把x家族挂在y家族后面 w[fx]=(w[x]+w[y])%2;//跟新关系数组 } } int main() { scanf("%d",&t); while(t--) { scanf("%d%d",&n,&m); for(int i=1;i<=n;i++) { //对当前的初始状态的各个节点分析其初始状态对应的状态数。 //我们设0代表当前节点与其父节点分属不同的团伙,1代表两者来自同一团体 //初始化的时候,每个节点的根节点都来自自己,而自己与自己当然是属于同一团伙 //所以全部初始化为1。 f[i]=i;w[i]=1; } char c;int a,b; while(m--) { scanf(" %c%d%d",&c,&a,&b); if(c=='D') join(a,b); else { if(find(a)!=find(b))printf("Not sure yet.\n"); else if((w[a]+w[b])%2)printf("In different gangs.\n"); else printf("In the same gang.\n"); } // for(int i=0;i<n;++i) // { // cout<<"father:"<<"f["<<i<<"]="<<f[i]<<","<<"关系:"<<"w["<<i<<"]="<<w[i]<<endl; // } } } return 0; }
E - Wireless Network
这题实质上也是套并查集的模板,就是要注意分析条件:
- 首先这里的数据是不限数量的
- 用cin会导致超时
- 题目给出的d是一个范围值,相当于一个圆的半径,在圆内的点都可以互相连通
- 题目给的computer,是像一个图一样离散分布的
- 可以加进并查集的前提是他依旧被修复好了并且两点之间的距离小于等于d
#include<iostream> #include<cmath> #include<string.h> #define MAX 1005 using namespace std; int set[MAX],height[MAX]; double dir[MAX][MAX]; int d,n,m,x,y; struct a { double x; double y; int tag; }point[MAX]; void init_set() { for(int i=0;i<=MAX;++i) { set[i]=i; height[i]=0; } memset(point,0,sizeof(struct a)*MAX); memset(dir,0,sizeof(double)*MAX*MAX); } int find_set(int x) { if(x!=set[x])set[x]=find_set(set[x]); return set[x]; } void union_set(int x,int y) { x=find_set(x); y=find_set(y); if(height[x]==height[y]) { height[x]+=1; set[y]=x; } else { if(height[x]<height[y])set[x]=y; else set[y]=x; } } int main() { init_set(); scanf("%d %d",&n,&d); for(int i=1;i<=n;++i)//所有的点都从1开始编号 { // cin>>point[i].x>>point[i].y;//输入坐标 scanf("%lf%lf",&point[i].x,&point[i].y); } for(int i=1;i<=n;++i) { for(int j=i+1;j<=n;++j) { dir[i][j]=sqrt(pow(point[i].x-point[j].x,2)+pow(point[i].y-point[j].y,2)); dir[j][i]=dir[i][j]; } }//计算各个点之间的距离 char opt[MAX]={}; getchar(); while(scanf("%s",&opt)!=EOF) { if(opt[0]=='O') { int a=0;scanf("%d",&a); point[a].tag=1;//修好了标记为1 for(int i=1;i<=n;++i) { if(point[i].tag&&i!=a&&!(dir[a][i]>d)) { union_set(i,a); } } } else if(opt[0]=='S') { int a=0,b=0;scanf("%d%d",&a,&b); if(find_set(a)==find_set(b)) { cout<<"SUCCESS"<<endl; } else { cout<<"FAIL"<<endl; } } } return 0; }
F - A Bug's Life
这题跟黑帮题很像,都是种类并查集的问题,套用到模板也是同一套。
- 设定的假设都是同性恋,因为自己跟自己咳咳,所以……
- 逻辑是:如果自己跟父亲相反,父亲跟爷爷相反,则自己跟爷爷相同
- 在找同性恋的时候,如果大家都是属于一个家族的就是彼此之间存在逻辑联系那么就开始判断,如果二者都是0那么就代表存在同性恋
y#include<iostream> #include<cstdio> #include<cstring> using namespace std; const int N=1e5+10; int t,n,m,f[N],w[N],flag=0;//w代表了当前节点与其父节点的关系 int find(int x) { if(x==f[x]) return x; int temp=f[x];//存放一下x的父亲 f[x]=find(f[x]);//路径压缩 w[x]=(w[x]+w[temp])%2;//跟新x和他祖先的关系 return f[x]; } void join(int x,int y) { int fx=find(x),fy=find(y); // cout<<">>"<<x<<"\n"; // for(int i=1;i<=n;++i) // { // cout<<i<<"的父亲:"<<f[i]<<",与父亲的关系:"<<w[i]<<endl; // } // cout<<endl; if(fx!=fy) { f[fx]=fy;//把x家族挂在y家族后面 w[fx]=(w[x]+w[y]+1)%2;//跟新关系数组 } else { if(w[x]==w[y])flag=1;return; } // cout<<"<<\n"; // for(int i=1;i<=n;++i) // { // cout<<i<<"的父亲:"<<f[i]<<",与父亲的关系:"<<w[i]<<endl; // } // cout<<endl; } int main() { scanf("%d",&t); for(int kk=1;kk<=t;++kk) { scanf("%d%d",&n,&m); for(int i=1;i<=n;i++) { f[i]=i;w[i]=0;//1代表异性恋,0代表同性恋 } int a,b; flag=0; while(m--) { scanf("%d%d",&a,&b); join(a,b); // for(int i=1;i<=n;++i) // { // if(!w[i])flag=1;break; // } } printf("Scenario #%d:\n",kk); if(flag) { printf("Suspicious bugs found!\n"); } else { printf("No suspicious bugs found!\n"); } printf("\n"); } return 0; }
G - Cube Stacking
思路是用两个并查集,一个放爸爸,一个放儿子,但是超时了,Orz

#include<iostream> #include<cstdio> #include<cstring> using namespace std; const int N=30004; int p,n,m,f[N],S[N]; char t; int c; void Inital() { for(int i=0;i<N;++i)f[i]=i,S[i]=i; t='\0'; c=0; } int find(int x) { if(x==f[x]) return x; return find(f[x]); } void join(int x,int y) { int fx=find(x),fy=find(y); if(fx!=fy) { f[fx]=S[y]; S[y]=fx; } } int counts(int x) { if(x==f[x]) return c; c++; return counts(f[x]); } int main() { Inital();scanf("%d",&p);getchar(); for(int kk=1;kk<=p;++kk) { scanf("%c",&t);getchar(); if(t=='M') { scanf("%d %d",&n,&m); join(n,m); } else { scanf("%d",&n); c=0;counts(n); printf("%d\n",c); } getchar(); } return 0; }
拖了一篇大佬的答案:https://blog.csdn.net/gauss_acm/article/details/26298125
#include<iostream> #include<cstdio> #define Maxn 30010 using namespace std; int fa[Maxn],dis[Maxn],height[Maxn]; int findset(int x) { if(fa[x]!=x) { int t=fa[x]; fa[x]=findset(fa[x]); dis[x]+=dis[t]; } return fa[x]; } void unionset(int x,int y) { x=findset(x),y=findset(y);//找到父节点 if(x==y) return;//如果两个属于同一个集合就结束 fa[y]=x;//将y家族的挂在x家族上(父节点之间的挂) dis[y]=height[x];//跟新y(最后一个结点)到根节点的距离 height[x]+=height[y];//跟新x(新的父亲)的树高 cout<<">>"<<x<<","<<y<<endl; for(int i=0;i<10;++i) { cout<<"height["<<i<<"]="<<height[i]<<",dis["<<i<<"]="<<dis[i]<<","<<"fa["<<i<<"]="<<fa[i]<<endl; } } int main() { int p,a,b; char s; cin>>p; for(int i=0;i<Maxn;i++) fa[i]=i,dis[i]=0,height[i]=1; for(int i=0;i<p;i++) { cin>>s; if(s=='M') { cin>>a>>b;unionset(a,b); } else { cin>>a; int t=findset(a); cout<<height[t]-dis[a]-1<<endl; } } return 0; }
H - 食物链
贴一份大佬的解答,清晰易懂tql:https://blog.csdn.net/m0_37579232/article/details/79920785

看了思路写也wa了好几次,挂家族挂反了,应把第一个全家挂在第二个后面 (ノへ ̄、)
#include<iostream> #include<cstdio> #include<cstring> using namespace std; const int N=50005; int cc; int k,n,m,a,b,d,f[N],w[N],flag=0; int find(int x) { if(x==f[x]) return x; int temp=f[x]; f[x]=find(f[x]); w[x]=(w[x]+w[temp])%3; return f[x]; } void join(int x,int y) { int fx=find(x),fy=find(y); if(fx!=fy) { f[fy]=fx; w[fy]=(w[x]+3-w[y]+d-1)%3; } } int main() { scanf("%d%d",&n,&k); for(int i=1;i<=n;i++) { f[i]=i;w[i]=0; } for(int kk=1;kk<=k;++kk) { scanf("%d%d%d",&d,&a,&b); if(a>n||b>n){++cc;continue;} if(d==2) { if(a==b){++cc;continue;} if(find(a)==find(b)) { if((3+w[b]-w[a])%3!=1) { ++cc; } } else { join(a,b); } } else if(d==1) { if(find(a)==find(b)) { if((3+w[b]-w[a])%3!=0) { ++cc; } } else { join(a,b); } } } printf("%d",cc); return 0; }
I - Dragon Balls HDU - 3635
一开始直接在主函数部分维护龙珠的移动次数,没有很好的理解题意:当1号龙珠移动到2号城市中时,如果下一次再去移动1号龙珠到3号城市,那么2号龙珠也会随之移动,2号龙珠的移动次数默认增加!!!

#include<iostream> #include<cstdio> #include<cstring> using namespace std; const int N=10005; char c; int a,b; int t,n,q,f[N],w[N],s[N],flag=0; int find(int x) { if(x==f[x]) return x; f[x]=find(f[x]); return f[x];//离父秦有几个就有几个龙珠数 } void join(int x,int y)//y是新节点,也是最后的城市,也是老祖宗 { int fx=find(x),fy=find(y); if(fx!=fy) { f[fx]=fy;//将a移动到b号城市里 w[fy]+=w[fx];//b城里的龙珠数等于原来的加上a城的 } // for(int i=1;i<=n;++i) // { // cout<<">>"<<i<<"的父亲是:"<<f[i]<<",城里的龙珠数:"<<w[i]<<",传输次数:"<<s[i]<<endl; // } } int main() { scanf("%d",&t); for(int tt=0;tt<t;++tt) { scanf("%d%d",&n,&q);getchar(); for(int i=1;i<=n;i++) { f[i]=i;w[i]=1;s[i]=0;//w存放第i个城市中的龙珠数量 } printf("Case %d:\n",tt+1); for(int kk=1;kk<=q;++kk) { scanf("%c",&c); if(c=='T') { scanf(" %d %d",&a,&b);getchar(); s[a]++;//传输次数自增 join(a,b); } else { scanf(" %d",&a);getchar(); int city=find(a); printf("%d %d %d\n",city,w[city],s[a]); } } } return 0; }
ac:
#include<iostream> #include<cstdio> #include<cstring> using namespace std; const int N=10005; char c; int a,b; int t,n,q,f[N],w[N],s[N]; int find(int x) { if(x==f[x]) return x; int temp=f[x]; f[x]=find(f[x]); s[x]+=s[temp]; return f[x]; } void join(int x,int y) { int fx=find(x),fy=find(y); if(fx!=fy) { f[fx]=fy; w[fy]+=w[fx]; s[fx]++; } } int main() { scanf("%d",&t); for(int tt=0;tt<t;++tt) { scanf("%d%d",&n,&q);getchar(); for(int i=1;i<=n;i++) { f[i]=i;w[i]=1;s[i]=0; } printf("Case %d:\n",tt+1); for(int kk=1;kk<=q;++kk) { scanf("%c",&c); if(c=='T') { scanf(" %d %d",&a,&b);getchar(); // s[a]++;//传输次数自增 join(a,b); } else { scanf(" %d",&a);getchar(); int city=find(a); printf("%d %d %d\n",city,w[city],s[a]); } } } return 0; }
J - More is better HDU - 1856
一发ac好开心ヾ(≧▽≦*)o,一开始看到5个0还以为会爆栈呢
#include<iostream> #include<algorithm> #include<cstdio> #include<cstring> using namespace std; const int N=10000001; char c; int a,b; int t,n,q,f[N],w[N]; int cmp(int a,int b) { return a>b; } int find(int x) { if(x==f[x]) return x; int temp=f[x]; f[x]=find(f[x]); // w[temp]+=w[x]; return f[x]; } void join(int x,int y) { int fx=find(x),fy=find(y); if(fx!=fy) { f[fx]=fy; w[fy]+=w[fx]; } // for(int i=1;i<12;++i) // { // cout<<i<<"的父亲是:"<<f[i]<<"此时圈中人数有:"<<w[f[i]]<<endl; // } } int main() { while(~scanf("%d",&t)) { for(int i=1;i<=N;i++) { f[i]=i;w[i]=1;//保存i圈中的人数 } int max=1; for(int kk=1;kk<=t;++kk) { scanf("%d%d",&n,&q); join(n,q); } for(int j=1;j<N;++j) { if(max<w[j])max=w[j]; } printf("%d\n",max); } return 0; }
K - 小希的迷宫 HDU - 1272
憨憨wa了三天,后来看一个博主的才知道自己的Yes,NO都是大写。。。。。

#include<iostream>
#include<algorithm>
#include<cstdio>
#include<cstring>
using namespace std;
#define N 100005
int t,n,q,a,b,f[N],w[N],flag;
void intial()
{
for(int i=0;i<=N;++i)f[i]=i,w[i]=1;
flag=1;//默认是一棵树
}
int find(int a)
{
int r=a;
while(f[r]!=r)
r=f[r];
int i=a;
int j;
while(i!=r)
{
j=f[i];
f[i]=r;
i=j;
}
return r;
}
void join(int x,int y)
{
w[x]=0;w[y]=0;
int fx=find(x),fy=find(y);
if(fx!=fy)
{
f[fy]=fx;
}
else
{
flag=0;
}
}
int main()
{
while(~scanf("%d%d",&a,&b))
{
if(a==0&&b==0)
{
printf("Yes\n");continue;
}
intial();
if(a==-1&&b==-1)break;
join(a,b);
while(scanf("%d%d",&a,&b)&&a&&b)
{
join(a,b);
}
if(flag)
{
int c=0;
for(int i=1;i<=N;++i)
{
if(!w[i]&&(f[i]==i)) c++;
}
if(c==1)
{
printf("Yes\n");
}
else
{
printf("No\n");
}
}
else
{
printf("No\n");
}
}
return 0;
}
L - Is It A Tree? HDU - 1325
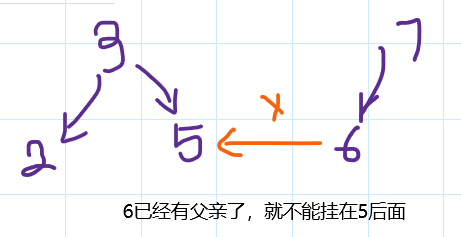
憨憨一开始只是简单的写了一个并查集来判断有没有环,并没有考虑周全,这是一个有向图,而简单的并查集是一个无向图
#include<iostream>
#include<algorithm>
#include<cstdio>
#include<cstring>
using namespace std;
#define N 100001
int t,n,q,a,b,f[N],w[N],flag;
void intial()
{
for(int i=0;i<=N;++i)
{
f[i]=i;
w[i]=0;
}
flag=0;//默认是一棵树
q=0;
}
int find(int a)
{
int r=a;
while(f[r]!=r)r=f[r];
int i=a;
int j;
while(i!=r)
{
j=f[i];
f[i]=r;
i=j;
}
return r;
}
void join(int x,int y)
{
w[x]=1;
w[y]=1;
int fx=find(x),fy=find(y);
if(fx!=fy)
{
f[fy]=fx;
q++;
}
else
{
flag=1;//判断环
}
}
int main()
{
int index=0;
while(~scanf("%d%d",&a,&b))
{
intial();
if(a<0&&b<0)break;
join(a,b);
index++;
printf("Case %d ",index);
if(a==0&&b==0)
{
printf("is a tree.\n");continue;
}
while(scanf("%d%d",&a,&b)&&a&&b)
{
if(a==b||f[b]!=b)flag=1;
//自己不能指向自己||已经有父亲了就不要再挂了
//树的根节点就只有一个
join(a,b);
}
if(flag)
{
printf("is not a tree.\n");
}
else
{
int cc=0;
for(int i=1;i<=N;++i)
{
if(w[i])cc++;//计算一下结点数量
}
if(cc==q+1)//n个结点的数中,边数只能是n-1条
{
printf("is a tree.\n");
}
else
{
printf("is not a tree.\n");
}
}
}
return 0;
}
M - Farm Irrigation HDU - 1198
- 一开始比较晕,想到要考虑四个方向什么的,后来参考了大佬的博客,发现如果先把这个图存起来在遍历就只用考虑2个方向(从左往右,从下到上)刚好是我们遍历二维数组的顺序
- 先不考虑所有的联通情况,把所有的格子都默认设定为不连通,这样就需要n*m个泉眼,发现连通的时候再一个一个删去就行了

#include<iostream>
#include<algorithm>
#include<cstdio>
#include<cstring>
#include<string>
using namespace std;
#define N 2550
int n,m,c,f[N];
string farm[N];
int map[11][4]={//左上右下顺时针
{1,1,0,0},//A
{0,1,1,0},//B
{1,0,0,1},//C
{0,0,1,1},//D
{0,1,0,1},//E
{1,0,1,0},//F
{1,1,1,0},//G
{1,1,0,1},//H
{1,0,1,1},//I
{0,1,1,1},//J
{1,1,1,1} //K
};
void intial(int a,int b)
{
for(int i=0;i<=(a*b+1);++i)f[i]=i;
c=0;
}
int find(int a)
{
int r=a;
while(f[r]!=r)r=f[r];
int i=a;
int j;
while(i!=r)
{
j=f[i];
f[i]=r;
i=j;
}
return r;
}
void join(int x1,int y1,int x2,int y2,int dir)
{
if(x2>=n||y2>=m)return;
int t1=farm[x1][y1]-'A';
int t2=farm[x2][y2]-'A';
int flag=0;
if(dir)//竖直方向-右边
{
if(map[t1][3]&&map[t2][1])flag=1;
}
else//水平方向-上边
{
if(map[t1][2]&&map[t2][0])flag=1;
}
if(flag)//只要有一个方向是可以连通的
{
int x=find(x1*m+y1+1);
int y=find(x2*m+y2+1);
if(x!=y)
{
f[y]=x;
--c;
}
}
}
int main()
{
while(~scanf("%d %d",&n,&m))
{
if(n<0||m<0)break;
intial(n,m);
for(int i=0;i<n;++i)
{
cin>>farm[i];
}
c=n*m;
for(int i=0;i<n;++i)
{
for(int j=0;j<m;++j)
{
join(i,j,i+1,j,1);
join(i,j,i,j+1,0);
}
}
printf("%d\n",c);
}
return 0;
}



