HDU | Friend Chains-4460 SPFA

题目：

Problem Description
For a group of people, there is an idea that everyone is equals to or less than 6 steps away from any other person in the group, by way of introduction. So that a chain of "a friend of a friend" can be made to connect any 2 persons and it contains no more than 7 persons.
For example, if XXX is YYY’s friend and YYY is ZZZ’s friend, but XXX is not ZZZ's friend, then there is a friend chain of length 2 between XXX and ZZZ. The length of a friend chain is one less than the number of persons in the chain.
Note that if XXX is YYY’s friend, then YYY is XXX’s friend. Give the group of people and the friend relationship between them. You want to know the minimum value k, which for any two persons in the group, there is a friend chain connecting them and the chain's length is no more than k .

Input
There are multiple cases.
For each case, there is an integer N (2<= N <= 1000) which represents the number of people in the group.
Each of the next N lines contains a string which represents the name of one people. The string consists of alphabet letters and the length of it is no more than 10.
Then there is a number M (0<= M <= 10000) which represents the number of friend relationships in the group.
Each of the next M lines contains two names which are separated by a space ,and they are friends.
Input ends with N = 0.

Output
For each case, print the minimum value k in one line.
If the value of k is infinite, then print -1 instead.

Sample Input
3
XXX
YYY
ZZZ
2
XXX YYY
YYY ZZZ
0

Sample Output
2

6
1
2
3
4
5
6
6
6 1
6 2
1
2
1 3
3 4
3 5

 

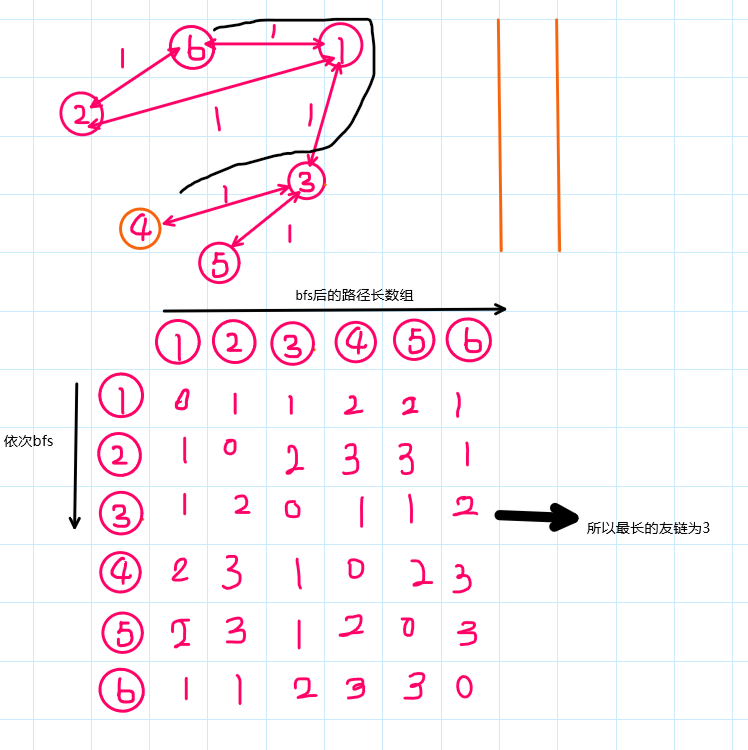
 答案：

源码来自： https://www.xuebuyuan.com/3265778.html

#include <cstdio>
#include <cstring>
#include <map>
#include <string>
#include <queue>
#include <vector>
#include <iostream>
#include <algorithm>

using namespace std;

const int maxn = 1005;
const int inf = 0x3f3f3f3f;

int N, Q, D[maxn];
vector<int> g[maxn];
map<string, int> idx;
queue<int> que;

int bfs(int s)
{
    memset(D, inf, sizeof(D));//direction数组初始化每一个值都赋为inf
    int ret = D[s] = 0;
    que.push(s);//把开始搜索的这个人入队

    while (!que.empty())
    {
        int u = que.front();
        que.pop();

        for (int i = 0; i < g[u].size(); i++)
        {
            //有可能u有多个朋友，所以这里设定为一个循环
            int v = g[u][i];//提取出u的朋友的下标
            if (D[v] > D[u] + 1) //边权都是为1的
            {
                //跟新direction数组
                D[v] = D[u] + 1;
                que.push(v);
            }
        }
    }

    //取得最短路中的最大值返回他
    for (int i = 1; i <= N; i++)
    {
        cout<<D[i]<<",";
        ret = max(ret, D[i]);
    }
    cout<<endl;
    return ret;
}

int main()
{
    while (scanf("%d", &N) == 1 && N)
    {
        idx.clear();
        string name, a, b;

        for (int i = 1; i <= N; i++)
        {
            g[i].clear();
            cin >> name;
            idx[name] = i;//记录它在数组中的位置
        }

        scanf("%d", &Q);
        for (int i = 0; i < Q; i++)
        {
            cin >> a >> b;
            g[idx[a]].push_back(idx[b]);//记录他朋友在数组中的位置
            g[idx[b]].push_back(idx[a]);//双向记录
        }

        int ans = 0;
        //对每一个i都进行了bfs;有几个人就(从他)bfs几次
        for (int i = 1; i <= N; i++)
        {
            cout<<i<<">>";
            ans = max(ans, bfs(i));
        }
        printf("%d\n", ans == inf ? -1 : ans);
    }
    return 0;
}

WAcode: 

一开始是打算在大佬的代码下改改的，后来发现根本不行，这种结构在处理环的适合相当麻烦

#include<iostream>
#include<queue>
#include<string>
#include<string.h>
#include<algorithm>
#define MAX_LENGTH 6 

using namespace std;
typedef struct f
{
    string name;
    int index;
    int my_friend_index[1002];
    int my_index;
}Friends;
Friends x[1002]; 
int n,m;
int length;
int Bfs(Friends x)
{
    queue<Friends> q;
    q.push(x);
    Friends temp;
    while(!q.empty())
    {
        temp=q.front();
        q.pop();
        for(int i=0;i<temp.index;++i)
        {
            if(CHRCK(temp.my_friend_index[i],temp.my_index))
            {
                //如果朋友链没到底，就将下一个人入队 
                ++length;
                q.push(x[temp.my_friend_index]);    
            } 
        if(x[temp.my_friend_index].my_friend_index==temp.my_index) return length;

        }
    } 
    return -1;
}
int main()
{
    while(scanf("%d",&n)!=EOF&&n)
    {
        if(!n)break;
        memset(x,0,sizeof(Friends)*1002);
        for(int i=1;i<=n;++i)
        {
            cin>>x[i].name;
            x[i].my_index=i;//记录下我的地址 
        }
        //输入人名 
        cin>>m;
        string one="",two="";
        int j,k;
        for(int i=0;i<m;++i)
        {
            cin>>one>>two;//输入两个人名 
            for(j=1;j<=n;++j)
            {
                if(one==x[j].name)
                {
                    break;    
                }
            }
            for(k=1;k<=n;++k)
            {
                if(two==x[k].name)
                {
                    break;
                }
            }
            x[j].my_friend_index[x[j].index]=k;//记录朋友在数组中的地址
            ++(x[j].index);
            x[k].my_friend_index[x[k].index]=j;//双向记录 
            ++(x[k].index);//有可能有多个朋友 
        }
        int result=-2;
        for(int j=1;j<=n;++i)
        {
            result=max(result,Bfs(x[i]);
        } 
        cout<<result<<endl;
    }
    
    return 0;
}