第二周训练 | 搜索技术 4.3 BFS
A - Red and Black
There is a rectangular room, covered with square tiles. Each tile is colored either red or black. A man is standing on a black tile. From a tile, he can move to one of four adjacent tiles. But he can't move on red tiles, he can move only on black tiles.
Write a program to count the number of black tiles which he can reach by repeating the moves described above.
Write a program to count the number of black tiles which he can reach by repeating the moves described above.
InputThe input consists of multiple data sets. A data set starts with a line containing two positive integers W and H; W and H are the numbers of tiles in the x- and y- directions, respectively. W and H are not more than 20.
There are H more lines in the data set, each of which includes W characters. Each character represents the color of a tile as follows.
'.' - a black tile
'#' - a red tile
'@' - a man on a black tile(appears exactly once in a data set)
OutputFor each data set, your program should output a line which contains the number of tiles he can reach from the initial tile (including itself).
Sample Input
6 9
....#.
.....#
......
......
......
......
......
#@...#
.#..#.
11 9
.#.........
.#.#######.
.#.#.....#.
.#.#.###.#.
.#.#..@#.#.
.#.#####.#.
.#.......#.
.#########.
...........
11 6
..#..#..#..
..#..#..#..
..#..#..###
..#..#..#@.
..#..#..#..
..#..#..#..
7 7
..#.#..
..#.#..
###.###
...@...
###.###
..#.#..
..#.#..
0 0
Sample Output
45 59 6 13
DFS:
#include<iostream> #include<cstdio> #include<queue> using namespace std; char room[25][25]; int dir[4][2]={{-1,0},{0,-1},{1,0},{0,1}}; int Wx,Hy,num; //Wx,Hy:长宽的边界 ，num:从初始瓷砖到能到达的瓷砖的总数 #define CHECK(x,y) (x<Wx&&x>=0&&y>=0&&y<Hy) //检查是否越界 struct node { int x,y; }; void DFS(int dx,int dy) { room[dx][dy]='#'; // cout<<"walk:"<<dx<<","<<dy<<endl; num++; for(int i=0;i<4;++i) { int newx=dx+dir[i][0]; int newy=dy+dir[i][1]; if(CHECK(newx,newy)&&room[newx][newy]=='.') { DFS(newx,newy); // cout<<" back:"<<dx<<","<<dy<<endl; } } } int main() { int x,y,dx,dy; //dx,dy： 人的站位 while(cin>>Wx>>Hy) { if(Wx==0&&Hy==0) { break; } for(y=0;y<Hy;++y) { for(x=0;x<Wx;++x) { cin>>room[x][y]; if(room[x][y]=='@') { dx=x; dy=y; } } } for(y=0;y<Hy;++y) { for(x=0;x<Wx;++x) { cout<<room[x][y]; } cout<<endl; } num=0; DFS(dx,dy); cout<<num<<endl; } return 0; }
BFS:
#include<iostream>
#include<cstdio>
#include<queue>
using namespace std;
char room[25][25];
int dir[4][2]={{-1,0},{0,-1},{1,0},{0,1}};
int Wx,Hy,num;
//Wx,Hy:长宽的边界 ，num:从初始瓷砖到能到达的瓷砖的总数
#define CHECK(x,y) (x<Wx&&x>=0&&y>=0&&y<Hy)
//检查是否越界
struct node
{
int x,y;
};
void BFS(int dx,int dy)
{
queue<node> q;
node start,next;
start.x = dx;
start.y = dy;
q.push(start);//把当前节点入队
while(!q.empty())
{
start = q.front();
q.pop();
for(int i=0;i<4;++i)
{
next.x=start.x+dir[i][0];
next.y=start.y+dir[i][1];
if(CHECK(next.x,next.y)&&room[next.x][next.y]=='.')
{
room[next.x][next.y]='#';//标记一下当前节点已经走过了
num++;//步数自增
q.push(next);//将子节点入队
}
}
}
}
int main()
{
int x,y,dx,dy;
//dx,dy： 人的站位
while(cin>>Wx>>Hy)
{
if(Wx==0&&Hy==0)
{
break;
}
for(y=0;y<Hy;++y)
{
for(x=0;x<Wx;++x)
{
cin>>room[x][y];
if(room[x][y]=='@')
{
dx=x;
dy=y;
}
}
}
num=1;
BFS(dx,dy);
cout<<num<<endl;
}
return 0;
}
B - Catch That Cow
Farmer John has been informed of the location of a fugitive cow and wants to catch her immediately. He starts at a point N (0 ≤ N ≤ 100,000) on a number line and the cow is at a point K (0 ≤ K ≤ 100,000) on the same number line. Farmer John has two modes of transportation: walking and teleporting.
* Walking: FJ can move from any point X to the points X - 1 or X + 1 in a single minute
* Teleporting: FJ can move from any point X to the point 2 × X in a single minute.
If the cow, unaware of its pursuit, does not move at all, how long does it take for Farmer John to retrieve it?
Input
Line 1: Two space-separated integers: N and K
Output
Line 1: The least amount of time, in minutes, it takes for Farmer John to catch the fugitive cow.
Sample Input
5 17
Sample Output
4
Hint
The fastest way for Farmer John to reach the fugitive cow is to move along the following path: 5-10-9-18-17, which takes 4 minutes.
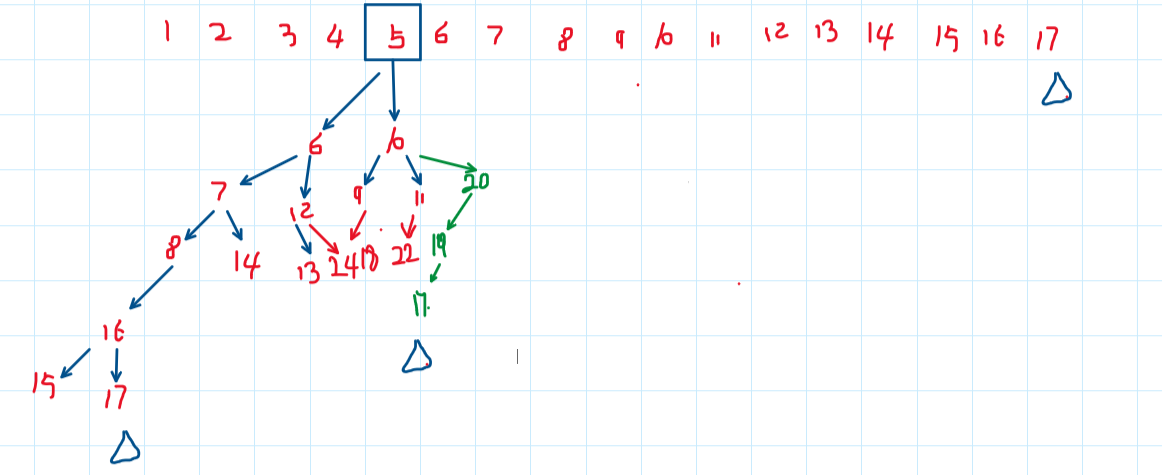
#include<iostream>
#include<string.h>
#include<queue>
using namespace std;
int to[2]={1,-1};
int a,b,sum;
int vis[100000];
struct place
{
int x,time;
};
int check(place k)
{
if(k.x<0||k.x>100000||vis[k.x]==1)
return 0;
return 1;
}
int bfs(place n)
{
place m,next;
queue<place>w;
w.push(n);
while(!w.empty())
{
m=w.front();
w.pop();
if(m.x==b)
return m.time;
for(int i=0;i<2;i++)
{
next.x=m.x+to[i];
next.time=m.time+1;
if(next.x==b)
return next.time;
if(check(next))
{
w.push(next);
vis[next.x]=1;
}
}
next.x=m.x*2;
next.time=m.time+1;
if(next.x==b)
return next.time;
if(check(next))
{
w.push(next);
vis[next.x]=1;
}
}
return 0;
}
int main()
{
int i,j,t;
place x1;
while(~scanf("%d %d",&a,&b))
{
x1.x=a;
x1.time=0;
vis[x1.x]=1;
sum=0;
sum=bfs(x1);
printf("%d\n",sum);
}
return 0;
}
第一次的awful代码：
感觉不足之处就在于我的记录步长的没有跟每一个节点一一对应，用结构体的化每一次遍历都可以得到到达当前节点的时间，这样多次累加后就可以得到通用时间，而我这里用的是num去更新result，虽然不知道哪里有问题，但是不如上面解法思路清晰，而且多次更新result容易超时,而且在操作多个数组的时候，结构体比数组更快：
作者：刘子昂在频繁操作同一个节点的情况下，用结构体更快。
用数组的那个方案是缓存不友好的，因为每次读写不同的数组都更可能无法命中缓存，从而产生额外的缓存IO操作。而用结构体的话，这个结构体整个都会被加载进缓存里（只要不是超大的结构体），程序每次读写结构体都是直接对缓存进行修改，再加上编译器的寄存器优化，这个性能就秒杀数组方案了。当然这里的“秒杀”是夸张手法，绝大多数情况下，cache missing不会产生显著的性能差异，除非真的是性能要求特别变态的场景。
链接：https://www.zhihu.com/question/285229473/answer/442702496
#include<iostream> #include<cstdio> #include<queue> using namespace std; #define LEN 1000000 int dir[3]={-1,1,2}; int Wx,Hy,num; //检查是否访问过 int mark[LEN]; int dx,dy; int result=LEN; struct node { int number; int steep; }; bool flag(int x,int y) { if(x>y) { return true; } else { return false; } } bool CHECK(int x) { if(!mark[x]) { mark[x]=1; return true; } else { return false; } } void BFS(int dx) { queue<int> q; int start; q.push(dx);//把当前人的位置入队 CHECK(dx); while(!q.empty()) { start = q.front(); q.pop(); // cout<<"当前出队："<<start<<endl; // cout<<"当前的步长是："<<num<<endl; for(int i=0;i<3;++i) { int temp=0; if(dir[i]==2) { temp=start*dir[i]; } else { temp=start+dir[i]; } if(flag(dx,dy)&&temp>dx) { //当牛在人的左边时，人要往左边走 continue; } if(!flag(dx,dy)&&temp<dx) { //当牛在人的右边时，人要往右边走 continue; } if(temp==dy) { if(result>num&&num!=0) result=num; num=0; continue; } else if(CHECK(temp)&&temp>=0&&temp<dy*2) { //如果没有访问过就入队 q.push(temp); } } num++; } return ; } int main() { //dx,dy： 人的站位和牛的站位 cin>>dx>>dy; num=0; BFS(dx); cout<<result; return 0; }
C - Find The Multiple
Given a positive integer n, write a program to find out a nonzero multiple m of n whose decimal representation contains only the digits 0 and 1. You may assume that n is not greater than 200 and there is a corresponding m containing no more than 100 decimal digits.
Input
The input file may contain multiple test cases. Each line contains a value of n (1 <= n <= 200). A line containing a zero terminates the input.
Output
For each value of n in the input print a line containing the corresponding value of m. The decimal representation of m must not contain more than 100 digits. If there are multiple solutions for a given value of n, any one of them is acceptable.
Sample Input
2
6
19
0
Sample Output
10
100100100100100100
111111111111111111
这题只要输出的结果对就行，没有统一答案。
#include<iostream>
using namespace std;
int flag=1;
void dfs(long long temp,int num,int count)
{
// cout<<"temp="<<temp<<" count="<<count<<endl;
if(flag==0) return;
if(count>18) return;//long long 越界
if(temp%num==0)
{
flag=0;
cout<<temp<<endl;
return;
}
dfs(temp*10,num,count+1);
dfs(temp*10+1,num,count+1);
return;
}
int main()
{
int n;
while(1){
cin>>n;
flag=1;
if(n==0) break;
dfs(1,n,0);
}
return 0;
}
D - Prime Path
The ministers of the cabinet were quite upset by the message from the Chief of Security stating that they would all have to change the four-digit room numbers on their offices.
— It is a matter of security to change such things every now and then, to keep the enemy in the dark.
— But look, I have chosen my number 1033 for good reasons. I am the Prime minister, you know!
— I know, so therefore your new number 8179 is also a prime. You will just have to paste four new digits over the four old ones on your office door.
— No, it’s not that simple. Suppose that I change the first digit to an 8, then the number will read 8033 which is not a prime!
— I see, being the prime minister you cannot stand having a non-prime number on your door even for a few seconds.
— Correct! So I must invent a scheme for going from 1033 to 8179 by a path of prime numbers where only one digit is changed from one prime to the next prime.
Now, the minister of finance, who had been eavesdropping, intervened.
— No unnecessary expenditure, please! I happen to know that the price of a digit is one pound.
— Hmm, in that case I need a computer program to minimize the cost. You don't know some very cheap software gurus, do you?
— In fact, I do. You see, there is this programming contest going on... Help the prime minister to find the cheapest prime path between any two given four-digit primes! The first digit must be nonzero, of course. Here is a solution in the case above.
— It is a matter of security to change such things every now and then, to keep the enemy in the dark.
— But look, I have chosen my number 1033 for good reasons. I am the Prime minister, you know!
— I know, so therefore your new number 8179 is also a prime. You will just have to paste four new digits over the four old ones on your office door.
— No, it’s not that simple. Suppose that I change the first digit to an 8, then the number will read 8033 which is not a prime!
— I see, being the prime minister you cannot stand having a non-prime number on your door even for a few seconds.
— Correct! So I must invent a scheme for going from 1033 to 8179 by a path of prime numbers where only one digit is changed from one prime to the next prime.
Now, the minister of finance, who had been eavesdropping, intervened.
— No unnecessary expenditure, please! I happen to know that the price of a digit is one pound.
— Hmm, in that case I need a computer program to minimize the cost. You don't know some very cheap software gurus, do you?
— In fact, I do. You see, there is this programming contest going on... Help the prime minister to find the cheapest prime path between any two given four-digit primes! The first digit must be nonzero, of course. Here is a solution in the case above.
1033The cost of this solution is 6 pounds. Note that the digit 1 which got pasted over in step 2 can not be reused in the last step – a new 1 must be purchased.
1733
3733
3739
3779
8779
8179
Input
One line with a positive number: the number of test cases (at most 100). Then for each test case, one line with two numbers separated by a blank. Both numbers are four-digit primes (without leading zeros).
Output
One line for each case, either with a number stating the minimal cost or containing the word Impossible.
Sample Input
3
1033 8179
1373 8017
1033 1033
Sample Output
6
7
0
#include<iostream>
#include<queue>
#include<string.h>
using namespace std;
int start,finish,prime[10001]={1,1,0},vis[10001];
struct node
{
int cur;//保存当前的素数
int step;
};
// init():生成一张素数表：不是素数标记为1，是素数标记为0
void init(){
for(int i=2;i<10001;i++)
{
if(!prime[i])
{
for(int j=2;i*j<10001;j++)
prime[i*j] = 1;
}
}
}
int BFS(){
queue<node>q;
vis[start]=1;
node m,n;
m.cur=start;
m.step=0;
q.push(m);
//将第一个素数入队
while(!q.empty())
{
int i,j;
char num[5];
m = q.front();
q.pop();
if(m.cur==finish) return m.step;
for(i=0;i<4;i++)
{
sprintf(num,"%d",m.cur);//sprintf主要功能是把格式化的数据写入某个字符串中
for(j=0;j<10;j++)
{
if(j==0&&i==0) continue;//如果不是四位数就过
if (i == 0)
n.cur = j * 1000 + (num[1] - '0') * 100 + (num[2] - '0') * 10 + (num[3] - '0');//第一位数字的1-9遍历
else if (i == 1)
n.cur =(num[0] - '0') * 1000 + j * 100 + (num[2] - '0') * 10 + (num[3] - '0');//第二位数字的1-9遍历
else if (i == 2)
n.cur =(num[0] - '0') * 1000 + (num[1] - '0') * 100 + j * 10 + (num[3] - '0');//第三位数字的1-9遍历
else if (i == 3)
n.cur =(num[0] - '0') * 1000 + (num[1] - '0') * 100 + (num[2] - '0') * 10 + j ;//第四位数字的1-9遍历
if(!prime[n.cur]&&!vis[n.cur])
{
//如果是素数并且没有访问过
//当前这个数入队，并且记录到达它的步长
n.step=m.step+1;
vis[n.cur]=1;
q.push(n);
}
}
}
}
return -1;
}
int main()
{
int t,x;
cin>>t;
init();
while(t--)
{
cin>>start>>finish;
memset(vis, 0, sizeof(vis));
x=BFS();
if(x == -1) cout<<"Impossible"<<endl;
else cout<<x<<endl;
}
return 0;
}
E - Pots
这题要注意的是visited数组要开到100开外
You are given two pots, having the volume of A and B liters respectively. The following operations can be performed:
- FILL(i) fill the pot i (1 ≤ i ≤ 2) from the tap;
- DROP(i) empty the pot i to the drain;
- POUR(i,j) pour from pot i to pot j; after this operation either the pot j is full (and there may be some water left in the pot i), or the pot i is empty (and all its contents have been moved to the pot j).
Write a program to find the shortest possible sequence of these operations that will yield exactly C liters of water in one of the pots.
Input
On the first and only line are the numbers A, B, and C. These are all integers in the range from 1 to 100 and C≤max(A,B).
Output
The first line of the output must contain the length of the sequence of operations K. The following K lines must each describe one operation. If there are several sequences of minimal length, output any one of them. If the desired result can’t be achieved, the first and only line of the file must contain the word ‘impossible’.
Sample Input
3 5 4
Sample Output
6
FILL(2)
POUR(2,1)
DROP(1)
POUR(2,1)
FILL(2)
POUR(2,1)
#include<iostream>
#include<queue>
#include<string>
using namespace std;
int As,Bs,Cs;
#define LEN 109
int visited[LEN][LEN];
string mark_list[6]={"FILL(1)\n","DROP(1)\n","POUR(1,2)\n","FILL(2)\n","DROP(2)\n","POUR(2,1)\n"};
struct pots
{
int A;
int B;
int steep;
string state;
};
queue<struct pots> q;
int bfs(int A,int B)
{
pots temp,head;
head.A=A;
head.B=B;
head.steep=0;
head.state="";
visited[A][B]=1;
q.push(head);
while(!q.empty())
{
head=q.front();
q.pop();
// cout<<"当前的锅(A,B+steep)："<<head.A<<" "<<","<<head.B<<"+"<<head.steep<<" state:"<<head.state<<endl;
if(head.A==Cs||head.B==Cs)
{
cout<<head.steep<<endl;
for(int i=0;i<head.state.length();++i)
{
cout<<mark_list[head.state[i]-'0'-1];
}
return 1;
}
for(int i=1;i<=6;++i)
{
temp=head;
// if(B>Bs||A>As)continue;
switch(i)
{
case 1:
temp.A=As;
break;
case 2:
temp.A=0;
break;
case 3:
if((Bs-temp.B)<=temp.A)
{
temp.A=temp.A-(Bs-temp.B);
temp.B=Bs;
}
else
{
temp.B+=temp.A;
temp.A=0;
}
break;
case 4:
temp.B=Bs;
break;
case 5:
temp.B=0;
break;
case 6:
if((As-temp.A)<=temp.B)
{
temp.B=temp.B-(As-temp.A);
temp.A=As;
}
else
{
temp.A+=temp.B;
temp.B=0;
}
break;
}
// cout<<i<<"操作后的锅(A,B+steep)："<<temp.A<<" "<<","<<temp.B<<"+"<<temp.steep<<" state:"<<temp.state<<endl;
if(visited[temp.A][temp.B]==0)
{
visited[temp.A][temp.B]=1;
temp.steep++;
temp.state+=i+'0';
q.push(temp);
}
}
};
return -1;
}
int main()
{
int A,B;
cin>>As>>Bs>>Cs;
int num=bfs(0,0);
if(num==-1)
{
cout<<"impossible"<<endl;
}
return 0;
}
