李宏毅机器学习课程笔记-10.4基于Smoothness假设的半监督学习
Smoothness假设
Smoothness假设的定义
基于Smoothness假设的半监督学习的基本思路是“近朱者赤近墨者黑”,即相似的\(x\)具有相同的\(\hat y\),其具体定义为:
- \(x\)的分布不平均,在某些地方(high density region)很集中,在某些地方很分散
- 如果\(x^1\)和\(x^2\)在一个high density region中距离非常近,则\(x^1\)和\(x^2\)通过1个high density path相连、\(\hat y^1=\hat y^2\)。
举一个例子,如下图所示,\(x^1,x^2,x^3\)是3个样本,如果单纯地看它们之间的相似度,显然\(x^2\)和\(x^3\)更接近一些。但对于smoothness assumption来说,\(x^1\)和\(x^2\)是位于同一个high density region中,它们之间有high density path;而\(x^2\)与\(x^3\)之间则是“断开”的,没有high density path,因此\(x^1\)与\(x^2\)更“像”。

手写数字识别举例
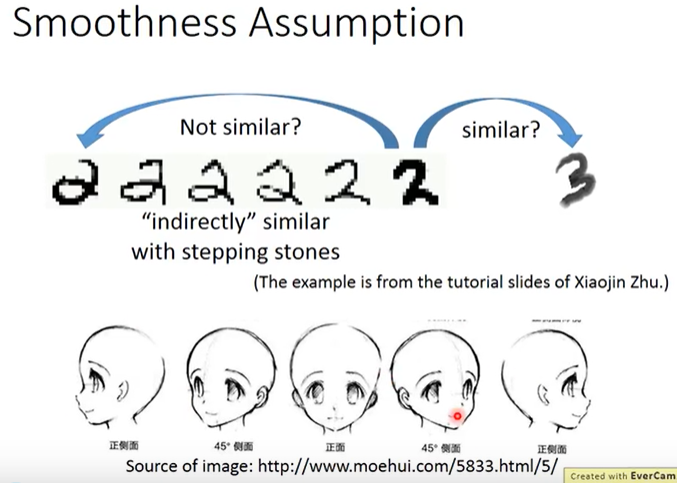
再举一个手写数字识别和人脸识别的例子,如下图所示,最左侧的2、最右侧的2和最右侧的3,从pixel角度来看明显是最右侧的2和3更加相似(尽管两者并非是同一个数字),但如果考虑最左侧的2朝着最右侧的2的演化过程,可以发现产生了一种“间接相似性”(high density path)。根据Smoothness假设,由于这6个2之间存在间接的相似而这6个2和最右侧的3之间不存在high density path,因此这6个2是彼此相似的;而最右侧的3和这6个2是不相似的。
文章分类举例
假设对天文学(astronomy)和旅行(travel)的文章进行分类,它们有各自的专属词汇,此时如果unlabeled data与label data的词汇是相同或重合(overlap)的,那么就很容易分类;但真实情况中unlabeled data和labeled data之间可能没有任何重复的word,因为世界上的词汇太多了,sparse的分布中overlap难以发生。
但如果unlabeled data足够多,就会以一种相似传递的形式,建立起文档之间相似的桥梁。
cluster and then label
如何实现基于Smoothness假设的半监督学习呢?在具体实现上,最简单的方式是cluster and then label。
cluster and then label就是先把所有样本(包括有标签样本和无标签样本)分成几个cluster,然后根据每个cluster中各类别有标签样本的数量确定该cluster中所有样本的label,然后进一步用这些cluster学习得到分类器。
这种方法不一定会得到好的结果,因为该方法有个前提是我们能够把同类别的样本分到同一个cluster,而这并不容易。对图像分类来说,如果仅仅依据pixel-wise相似度来划分cluster,得到的结果一般都会很差。所以为了满足这个前提,我们需要设计较好的方法来描述一张图片(比如使用Deep Autoencoder提取图片特征feature),以保证cluster时能够将同类别的样本分到同一个cluster。
Graph-based Approach
high density path
如何实现基于Smoothness假设的半监督学习呢?我们可以将每个样本视为图中的1个点,通过图来表示connected by a high density path。Graph-based方法的基本思路是图中的有标注样本会影响与它们邻近的无标注样本并在图中产生“间接相似性”,即使某些无标注样本没有直接与有标注样本相连也仍然可以被判定为相似。如果想要让这种方法生效,收集到的数据一定要足够多,否则可能导致无法形成path、失去了information的传递效果。
如何建立一张图
有时候点之间的边是比较好建立的(比如网页超链接、论文引用),有时候需要我们自行建立点之间的边。图的好坏对最终结果的影响是非常关键的,但如何建图是一件heuristic的事情,需要我们凭经验和直觉来做,建图步骤如下:
-
定义两个样本\(x^i,x^j\)之间的相似度计算方法\(s(x^i,x^j)\)
如果是基于pixel-wise的相似度,那结果可能比较差,建议使用更好的方法(比如使用Autoencoder提取图片特征,并基于提取到的特征计算相似度)。
推荐使用的相似度计算方法为高斯径向基函数(Gaussian Radial Basis Function):\(s(x^i,x^j)=exp(-\gamma||x^i-x^j||^2)\),其中\(x^i,x^j\)均为vector。经验上来说exp(exponential)通常是可以帮助提升性能的,因为它使得仅当\(x^i,x^j\)非常接近时similarity才会大、只要距离稍微远一点similarity就会迅速变小,也就是使用exponential可以做到只有非常近的两个点才能相连、稍微远一点就无法相连的效果。
-
建立点和点之间的边
-
k-Nearest Neighbor(K近邻算法)
在特征空间中,如果一个样本附近的k个最近样本的大多数属于某一类别,则该样本也属于这个类别
-
e-Neighborhood
-
-
设置点和点之间边的权重
一条边的权重应该和该边两个顶点的相似度成比例
如何定量地评估一个图符合Smoothness假设的程度
那如何定量地评估一个图符合Smoothness假设的程度呢?
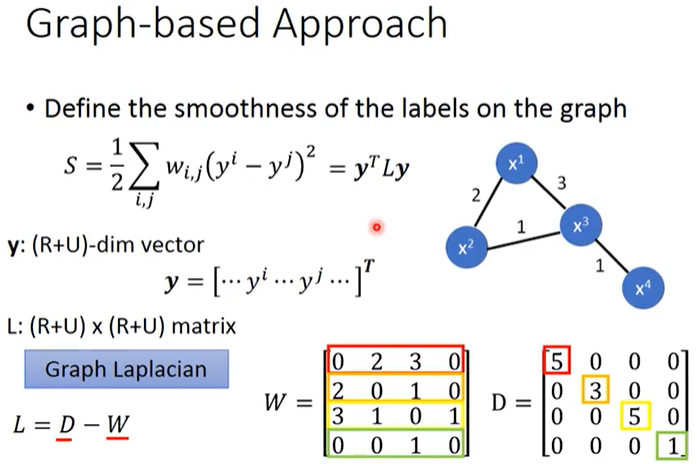
如上图所示,我们定义1个图的Smoothness为\(S=\frac{1}{2}\sum_{i,j}w_{i,j}(y^i-y^j)^2\)并希望它越小越好,其中\(i,j\)为所有样本点的索引、\(x^i\)表示样本的特征、\(y^j\)表示样本的标注(有可能是伪标签)、\(w_{i,j}\)是2个样本之间边的权重、\(\frac{1}{2}\)只是为了方便计算。
上式Smoothness定义还可以表示为\(S=y^TLy\),其中\(y\)是1个(R+U)-dim的vector:\(y=[\dots,y^i,\dots,y^j,\dots]^T\)、\(L\)是1个(R+U)×(R+U)的矩阵(名字叫做Graph Laplacian)。
Graph Laplacian的定义为\(L=D-W\),其中\(W_{i,j}\)为2个样本点之间边的权重,把\(W\)每行元素之和放在该行对应的对角线上其它元素值为0即可得到\(D\),如上图所示。在图神经网络(Spectral-based Convolution)中,有关于Graph Laplacian的介绍。
如何训练
Smoothness定义\(S=y^TLy\)中\(y\)是模型的输出(预测得到的类别),它是取决于模型参数的,因此训练时仅需在有标注数据的损失函数上加上Smoothness即可:\(L=\sum_{x^r}C(y^r,\hat y^r)+\lambda S\),其中\(\lambda S\)可以被视为正则项。
由上可知,训练目标为:
- 有标注数据的交叉熵越小越好,即模型的输出与标注越接近越好
- 所有数据的Smoothness越小越好,即不管是有标注数据还是无标注数据,模型输出都要符合Smoothness Assumption的假设
注:训练时可以不仅仅要求整个模型的输出层要smooth,还可以对模型中任意一个隐藏层加上smooth的限制。
Github(github.com):@chouxianyu
Github Pages(github.io):@臭咸鱼
知乎(zhihu.com):@臭咸鱼
博客园(cnblogs.com):@臭咸鱼
B站(bilibili.com):@绝版臭咸鱼
微信公众号:@臭咸鱼
转载请注明出处,欢迎讨论和交流!



