李宏毅机器学习课程笔记-2.2如何选择模型、减小误差

模型选择（How to select model）

• 模型越复杂，一般其在训练集上的误差（Error）越小。

  因为更复杂的模型（函数集）包含了更多的函数。比如二次模型包含了线性（一次）模型。

• 模型越复杂，其在测试集上的误差（Error）不一定越小。

  因为模型过于复杂时，越容易被数据影响，可能导致过拟合。

误差（Error）

误差的来源

暂时称通过机器学习得到的函数为人工函数，它其实是对“上帝函数”的估计（Estimator），和“上帝函数”之间是有误差的。

误差来源于两方面：一是Bias，二是Variance，需要权衡（trade-off）两者以使总误差最小。

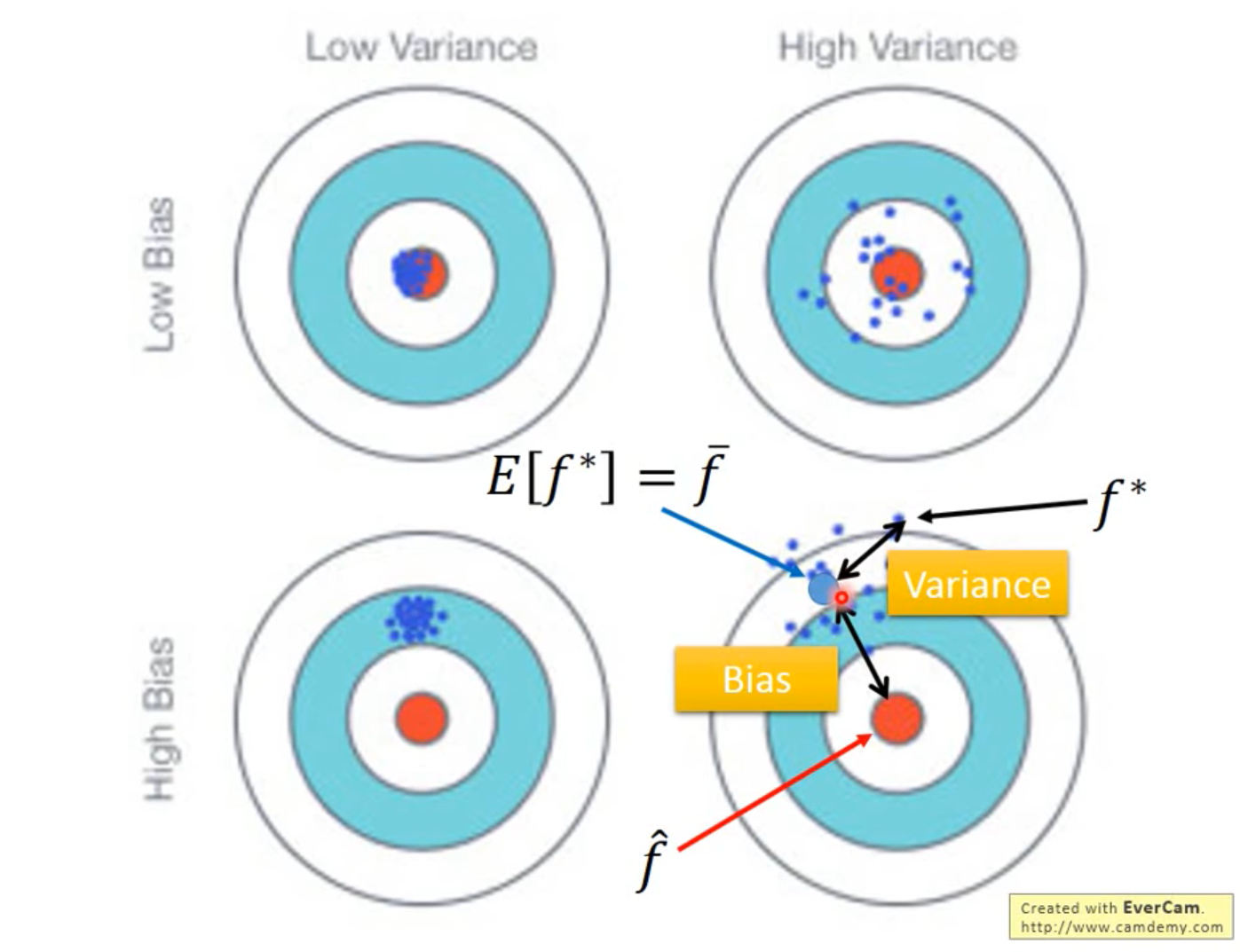
如上图所示，Bias是指人工函数（的期望）和上帝函数之间的距离，Variance是指人工函数的离散程度（或者说是不稳定程度）。

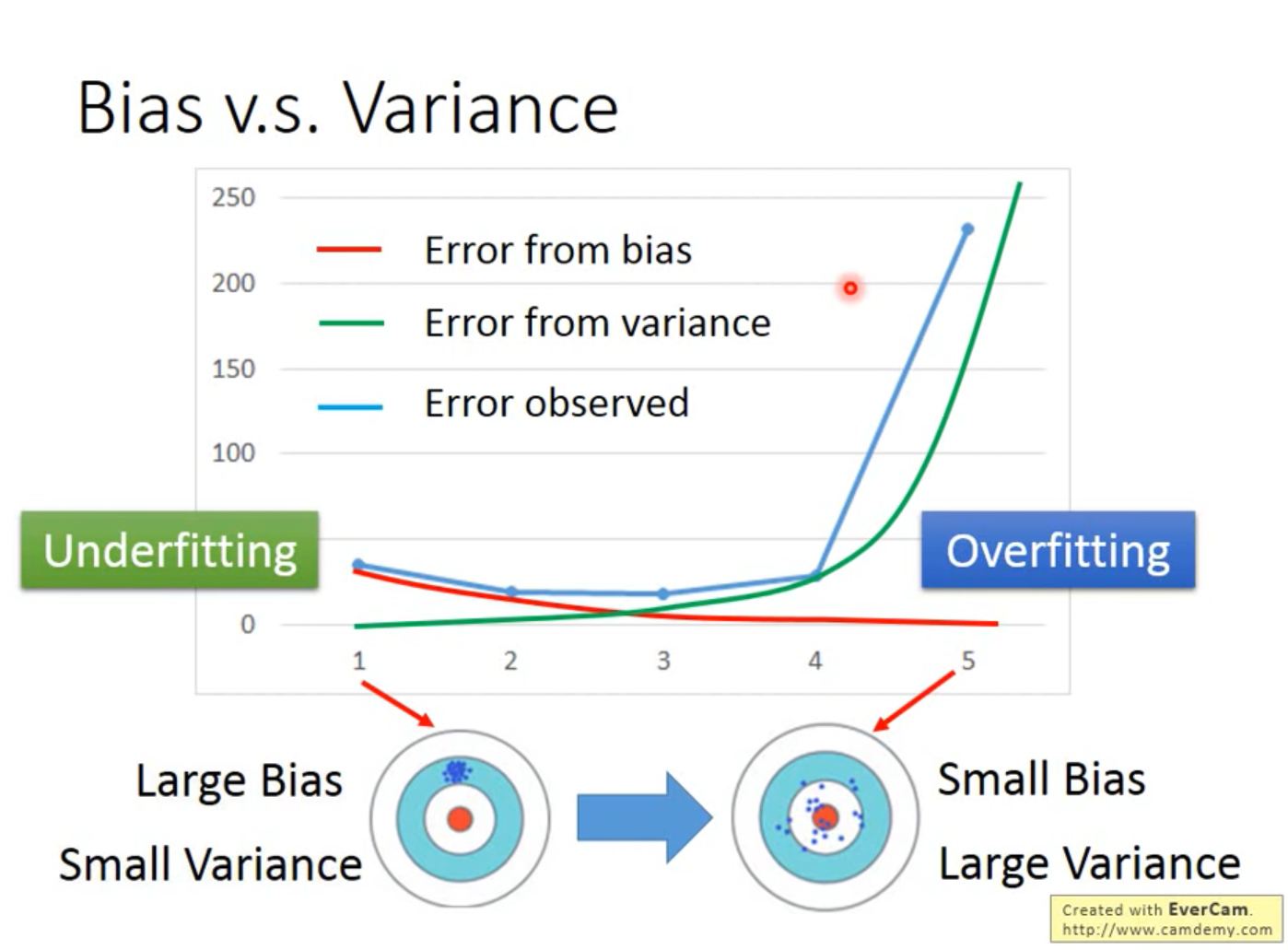
如上图所示，横轴是模型的复杂程度（1次幂、2次幂、……），纵轴是误差大小。模型越复杂，Bias越小，Variance越大。

Variance

定义

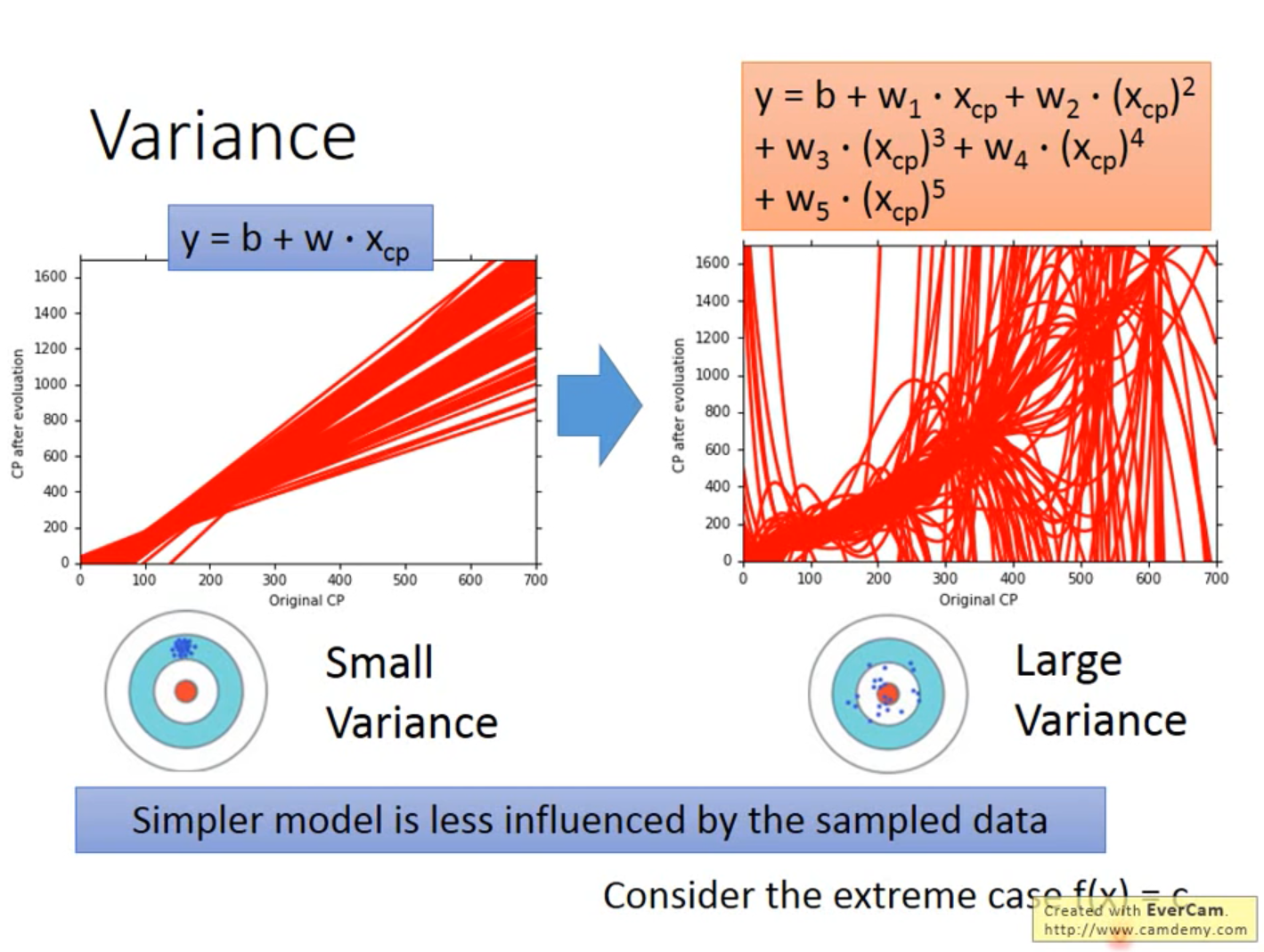
使用相同模型在不同数据上拟合得到的函数是不同的，这些函数之间的离散程度就是Variance。

以射箭为例，Variance衡量的就是射得稳不稳。

模型越复杂，Variance越大。

因为模型越简单，越不容易被数据影响（对数据不敏感，感知数据变化的能力较差），那Variance就越小。

Bias

定义

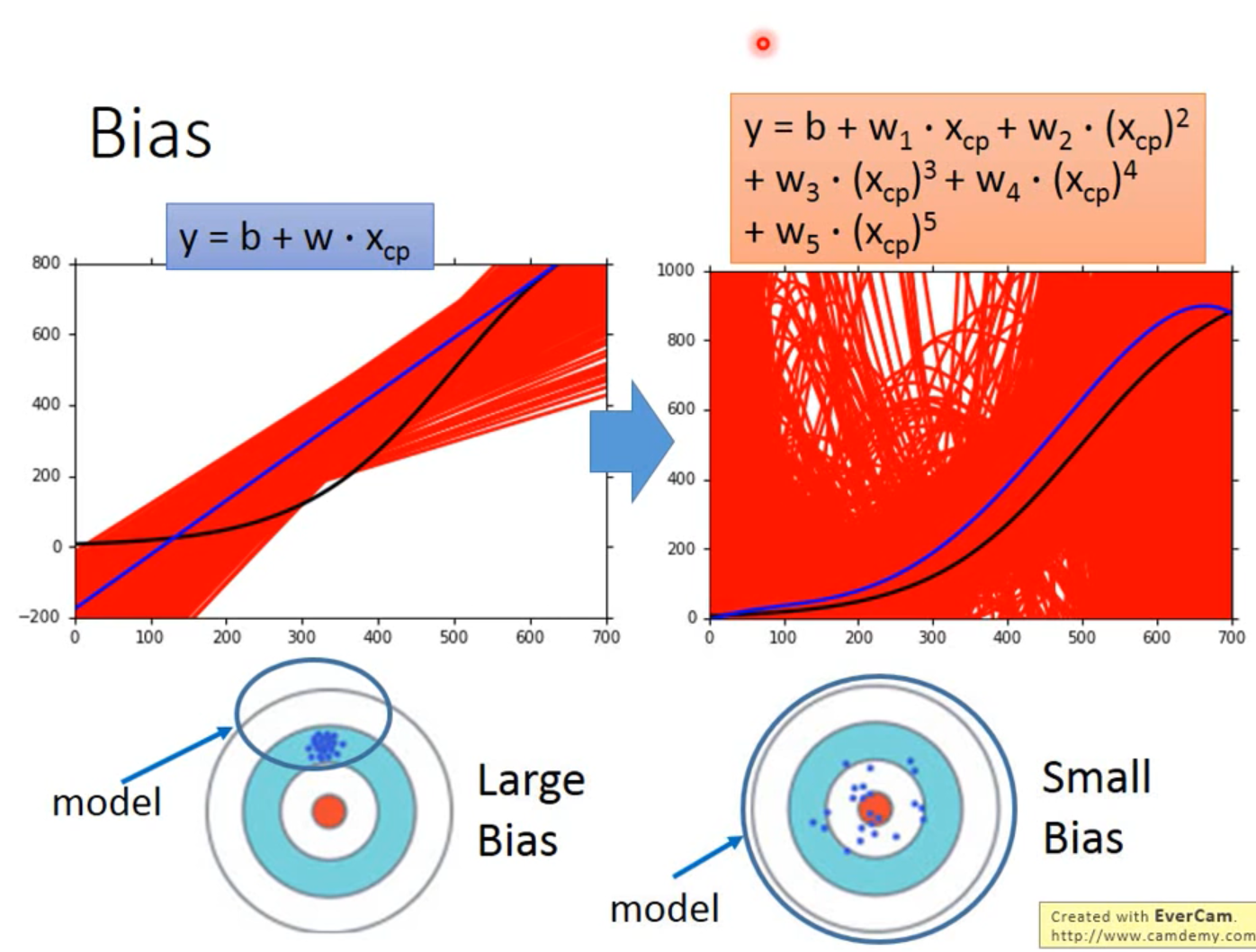
使用相同模型在不同数据上拟合得到的函数是不同的，取这些函数的“期望”，该期望与“真理”的差距就是Bias。

以射箭为例，Bias衡量的就是射得准不准（这里的“准”的含义有待商榷）。

模型越简单，Bias越大。

因为模型就是个函数集（Function Set）。模型越简单，则其包含的函数就越少、包含“上帝函数”的几率就越小，甚至可能不包括上帝函数。

在函数集很小的情况下，即使是其中最好的函数，它与“上帝函数”的差距也还是很大的。

---

Github（github.com）：@chouxianyu

Github Pages（github.io）：@臭咸鱼

知乎（zhihu.com）：@臭咸鱼

博客园（cnblogs.com）：@臭咸鱼

B站（bilibili.com）：@绝版臭咸鱼

微信公众号：@臭咸鱼的快乐生活

转载请注明出处，欢迎讨论和交流!

---