使用Python和OpenCV实现SIFT与ORB

目录如下：

目录

程序运行环境

  • python 3.7.3
  • numpy 1.16.6
  • opencv-python 4.4.0.40

SIFT_pratice.py

程序

import cv2
import numpy as np

"""
该程序使用dataset中的1.jpg和2.jpg，使用SIFT对这2张图片进行特征检测和特征提取，使用暴力匹配法对这2张图片进行特征匹配，最后计算匹配程度较高的特征点的单应性矩阵
"""

# 读取图片
img1 = cv2.imread('./dataset/1.jpg')
img2 = cv2.imread('./dataset/2.jpg')

# 创建SIFT
sift = cv2.xfeatures2d.SIFT_create()

# 检测关键点并提取特征
kp1, des1 = sift.detectAndCompute(img1, None)
kp2, des2 = sift.detectAndCompute(img2, None)

# 特征匹配：暴力匹配
bf = cv2.DescriptorMatcher_create(cv2.DescriptorMatcher_BRUTEFORCE)
matches = bf.match(des1, des2)

# 绘制特征匹配结果
matches = sorted(matches, key=lambda x: x.distance)
good_matches = matches[:50]  # 只取前XX个匹配
result = cv2.drawMatches(img1, kp1, img2, kp2, good_matches,
                         None, matchColor=(0, 0, 255), singlePointColor=(255, 0, 0))  # 只画前XX个匹配
cv2.imshow('result', result)

# 计算单应性矩阵
pts1, pts2 = [], []
for f in good_matches:
    pts1.append(kp1[f.queryIdx].pt)
    pts2.append(kp2[f.trainIdx].pt)
H, _ = cv2.findHomography(np.float32(pts1), np.float32(pts2), cv2.RHO)
print('单应性矩阵：')
print(H)

cv2.waitKey(0)

程序功能

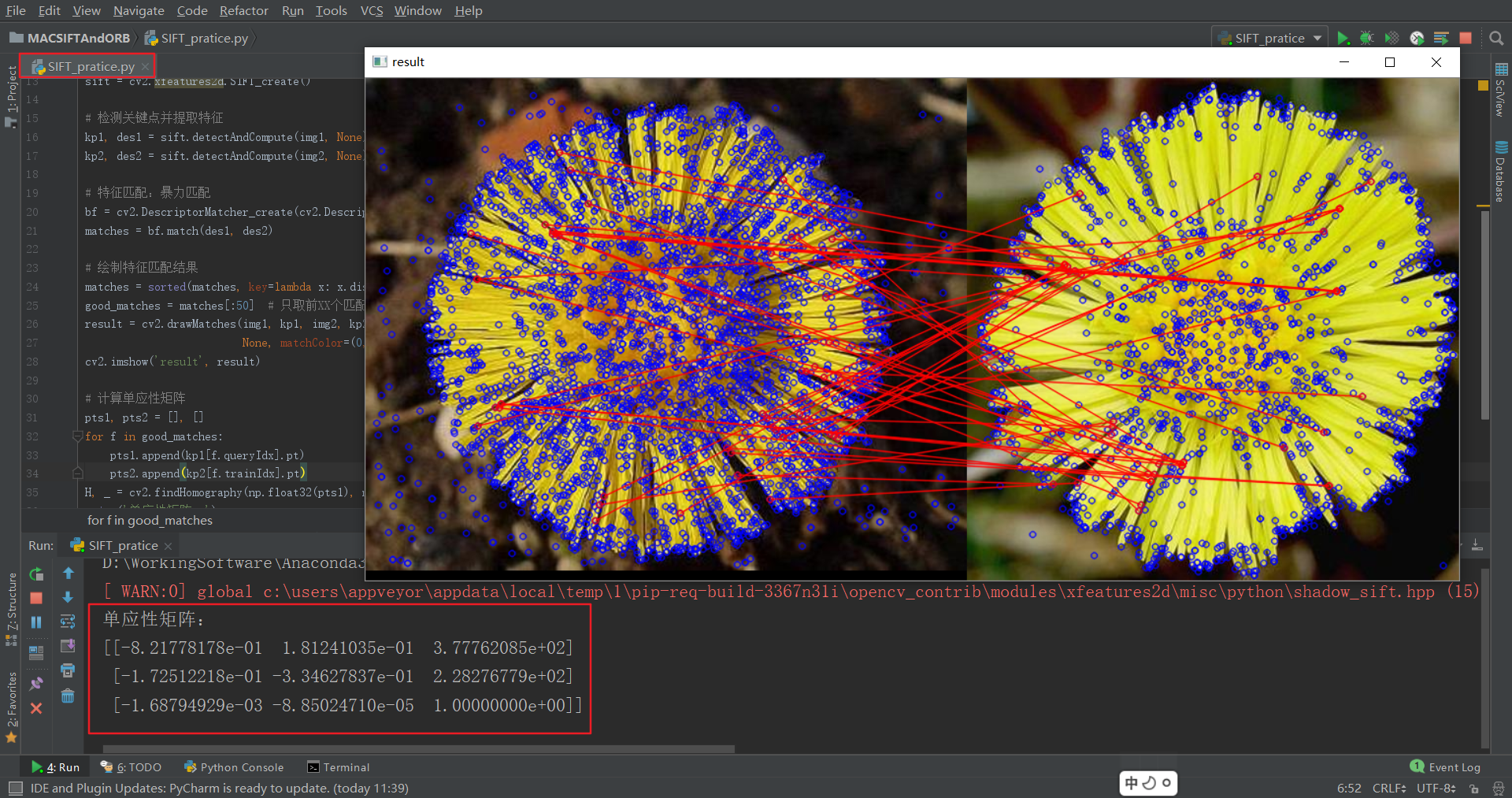
该程序使用dataset中的1.jpg和2.jpg，使用SIFT对这2张图片进行特征检测和特征提取，使用暴力匹配法对这2张图片进行特征匹配，最后计算匹配程度较高的特征点的单应性矩阵。

运行结果

SIFT_pratice运行结果

ORB_pratice.py

程序

import cv2
import numpy as np

"""
该程序使用dataset中的3.jpg和4.jpg，使用ORB对这2张图片进行特征检测和特征提取，使用暴力匹配法对这2张图片进行特征匹配，，最后计算匹配程度较高的特征点的单应性矩阵
"""

# 读取图片
img1 = cv2.imread('./dataset/3.jpg')
img2 = cv2.imread('./dataset/4.jpg')

# 创建ORB
orb = cv2.ORB_create()

# 检测关键点并提取特征
kp1, des1 = orb.detectAndCompute(img1, None)
kp2, des2 = orb.detectAndCompute(img2, None)

# 特征匹配：暴力匹配、汉明距离
bf = cv2.BFMatcher(cv2.NORM_HAMMING, crossCheck=True)
matches = bf.match(des1, des2)

# 绘制特征匹配结果
matches = sorted(matches, key=lambda x: x.distance)
good_matches = matches[:50]  # 只取前XX个匹配
result = cv2.drawMatches(img1, kp1, img2, kp2, good_matches, None)
cv2.imshow('result', result)

# 计算单应性矩阵
pts1, pts2 = [], []
for f in good_matches:
    pts1.append(kp1[f.queryIdx].pt)
    pts2.append(kp2[f.trainIdx].pt)
H, _ = cv2.findHomography(np.float32(pts1), np.float32(pts2), cv2.RHO)
print('单应性矩阵：')
print(H)

cv2.waitKey(0)

程序功能

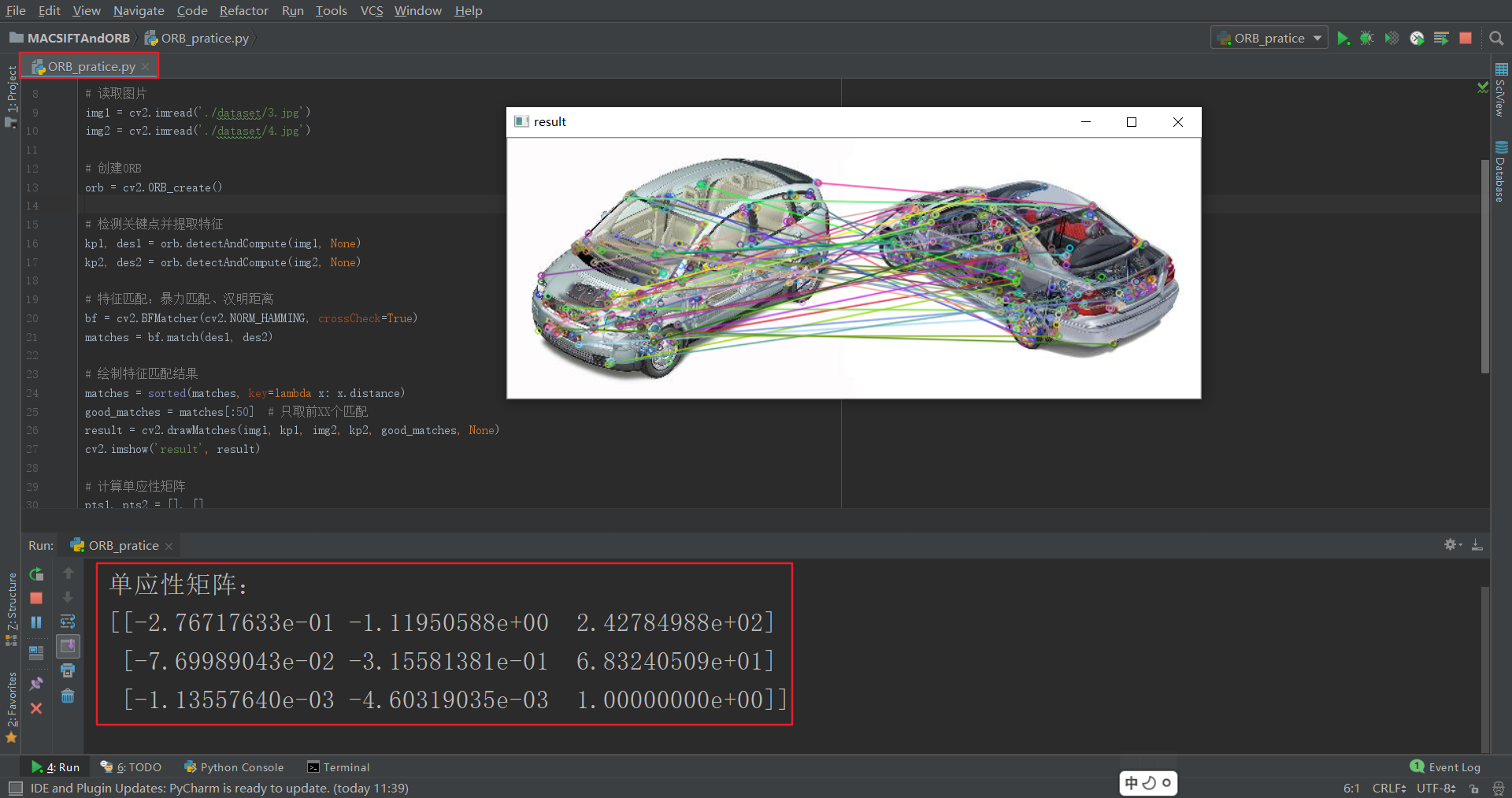
该程序使用dataset中的3.jpg和4.jpg，使用ORB对这2张图片进行特征检测和特征提取，使用暴力匹配法对这2张图片进行特征匹配，，最后计算匹配程度较高的特征点的单应性矩阵。

运行结果

ORB_pratice运行结果

相关理论

SIFT

  • 作者

    David Lowe

  • 发表

    David Lowe于1999年发表于ICCV，经过整理和完善，在2004年发表于IJCV。

  • 特点

    对图片大小和旋转不敏感，而且对光照、噪声等影响的抗击能力也非常优秀。

  • 实现

    可以分为4个步骤

    1. Scale-space extrema detection
      • 使用高斯差分函数（DoG）来计算并搜索所有尺度上的图像位置，用于识别对尺度和方向不变的潜在兴趣点。
      • 由于平滑区域临近像素之间变化不大，但是在边、角、点这些特征较丰富的地方变化较大，因此通过DOG比较临近像素可以检测出候选关键点。
    2. Keypoint localization
      • 通过一个拟合精细的模型在每个候选位置上确定位置和尺度，关键点的选择依赖于它们的稳定程度。
      • 根据关键点的稳定性来选择关键点。在每个候选位置，通过一个模型来确定位置和比例。
    3. Orientation assignment
      • 基于局部图像的梯度方向，将一个或多个方向分配给每个关键点位置。
      • 后续所有对图像数据的操作都是相对于关键点的方向、尺度和位置进行变换，从而为这些变换提供了不变性。
    4. Keypoint descriptor
      • 在每个关键点周围的区域内以选定的比例计算局部图像梯度，这些梯度被变换成一种表示。
      • 这种表示允许比较大的局部形状的变形和光照变化。

ORB

  • 作者

    Ethan Rublee在2011年发表于ICCV

  • 提出

    • SIFT算法

      不管是特征提取还是特征描述，SIFT都十分复杂，并且特征向量的匹配采用浮点数之间计算欧式距离，较为耗时。

    • FAST特征提取算法

      于2006年ECCV上提出，作为十分高效的特征点提取算法，其并没有提取出特征点的主方向，因而后续无法根据主方向对特征点进行描述。

    • BRIEF特征描述算法

      于2010年CVPR上提出，其是一种十分简单的特征点描述算法，其输出向量为二进制、进而极大的节省了向量的保存空间和简化了特征向量间的距离计算，但该算法对方向的改变十分敏感，因此对特征点的描述将不具有旋转不变性。

    • ORB

      ORB算法在FAST算法的基础上，提取了特征点的方向。同时根据特征点的方向，采用改进BRIEF算法的Rotated BRIEF算法对特征进行描述。ORB取长补短，既高效地完成了特征提取和特征描述，又使得特征描述向量具有旋转不变性。

  • 特点

  • 实现

    可以分为4个步骤

    1. 构造图像金字塔

      在不同降采样大小的图像下进行FAST特征点提取，进而得到特征点的尺度信息

    2. FAST算法

      1. 对于图像中一个像素点p，其灰度值为Ip
      2. 以该像素点为中心考虑一个半径为3的离散化的Bresenham圆，圆边界上有16个像素
      3. 设定一个合适的阈值t，如果圆上有n个连续像素点的灰度值小于Ip−t或者大于Ip+t，那么这个点即可判断为特征点（角点），n的值可取9、11、12。

      运行完FAST算法，会得到大量特征点，需要用NMS筛选

    3. 计算旋转角度

      • 利用灰度质心法求一个圆形区域的质心，连接质心和圆心形成一个向量，这个向量的角度就是角点的角度。
      • 其中圆的半径取为15，因为整个patch一般取的是31×31的。
      • 这个角度可以用来指导BRIEF描述子的提取，保证每次都在相同的方向上计算描述子，实现角度不变性。

    4. 计算旋转后的BRIEF描述子

      • BRIEF
        • 在特征点的描述区域范围（系数*尺度）内，随机生成256个位置对。对于每对位置，如果位置1点的像素值大于位置2点的像素值，则该对位置的输出为1，反之为0。
        • 一共有256个位置对，所以最终特征描述将用一个256向量组成，向量的每个元素都是二进制数。
        • 对于随机生成的256个位置对，BRIEF作者尝试了五种方法，最终选择二维高斯函数作为位置对的分布。
        • 位置对的生成为初始随机生成，但生成后位置对便固定下来，最终匹配的时候所有特征点均采用相同的位置对。
      • Steered BRIEF
        • BRIEF算法中，位置对是以右方向为x轴。
        • 在Steered BRIEF算法中，特征点的位置对以特征点的主方向为x轴，因此当主方向为θ时，原BRIEF算法中的位置对的位置也需要根据θ进行坐标转换。
          • 具体方法是已选好的256个位置对乘上旋转矩阵，从而得到以特征点的主方向为x轴时坐标系下的位置。
          • 通过该256个位置对对特征点进行描述，由于位置对的位置已经根据方向发生了相应的改变，因此Steered BRIEF算法具有一定的旋转不变性。
      • Rotated BRIEF
        • 在Steered BRIEF算法，其256维度的特征描述向量，每一个位置对的位置与其输出有一定的相关性，进而使得特征描述向量的信息熵减少。由此， Rotated BRIEF 提出用统计学习的方法选择位置对代替二维高斯随机分布选择位置对。

单应性变换

  • 单应性变换是什么

    • 单应性变换是一个平面内的点映射到另一个平面内的二维投影变换，对应的变换矩阵称为单应性矩阵。
    • 在这里，平面是指图像或者三维中的平面表面。

  • 单应性变换的作用

    单应性变换具有很强的实用性，比如图像配准，图像纠正和纹理扭曲，以及创建全景图像。

  • 关于齐次坐标

    • 对于图像平面内的点，齐次坐标是个非常有用的表示方式。
    • 点的齐次坐标是依赖于尺度定义的，所以x=[x,y,w]=[αx,αy,αw]=[x/w,y/w,1] 都表示同一个点。因此单应性矩阵H也依赖尺度定义。

作者：@臭咸鱼

转载请注明出处：https://www.cnblogs.com/chouxianyu/

欢迎讨论和交流!

posted @ 2020-10-19 19:07  臭咸鱼  阅读(2881)  评论(2)  编辑  收藏  举报