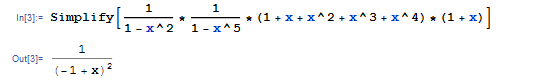母函数入门笔记（施工中…

定义：对于一个数列a_i，它的母函数（即生成函数）为G(x)=\sum_{i=0}^{\infty}a_i*x^i

 

为了对这个G(x)准确求值，我们设-1<x<1\&x\neq0 

 

举一个简单的例子

例1

对于数列a_i=1

他的生成函数为G(x)=\sum_{i=0}^{\infty}x^i ，那么应用一下等比数列求和公式

G(x)=\sum_{i=0}^{\infty}x^i=a_1*\frac{1-x^n}{1-x}

这里由于-1<x<1\&x\neq0

所以当n\to\infty时x^n\to0

那么G(x)=\sum_{i=0}^{\infty}x^i=a_1*\frac{1-x^n}{1-x}=\frac{1}{1-x}

 

例2

对于数列a_i=b^i

生成函数G(x)=\sum_{i=0}^{\infty}b^i*x^i

就是上面那个的比例系数放大到b

那么就是G(x)=\sum_{i=0}^{\infty}b^i*x^i=\frac{1}{1-bx}

例3

对于数列a_i=i\%2

生成函数G(x)=\sum_{i=0}^{\infty}x^{2i}

就是比例系数放大到x^2

可以得出G(x)=\sum_{i=0}^{\infty}x^{2i}=\frac{1}{1-x^2}

类比可以得到G(x)=\sum_{i=0}^{\infty}x^{ki}=\frac{1}{1-x^k}

 

例4

然后是一个很鬼的

对于数列a_i=i+1求生成函数G(x)=\sum_{i=0}^{\infty}(i+1)x^{i}

我们考虑这个东西是在无限定义下的

所以G(x)=\sum_{i=0}^{\infty}(i+1)x^{i}等价于G(x)=(\sum_{i=0}^{\infty}x^i)^2=\frac{1}{(1-x)^2}

同时可以扩展到

G(x)=\sum_{i=0}^{\infty}\begin{pmatrix}i+m-1\\m-1\end{pmatrix}x^{i}=\sum_{i=0}^{\infty}(\frac{1}{1-x})^m

例5

然后是一个稍微麻烦点的

对于数列a_i=i^2求生成函数

 

然后为了把这个东西化简成我们知道的。。就把它用导数公式乱套套

 

G(x)=\sum_{i=0}^{\infty}i^2x^i=(\sum_{i=0}^{\infty}nx^n)'*x

=((\sum_{i=0}^{\infty}(n+1)x^n)*x)'*x=(\frac{1}{(1-x)^2}*x)'*x=\frac{x(x+1)}{(1-x)^3}

 

一个实例

image

找规律超快的

我们分四个水果的情况求下生成函数

G_A(x)=\sum_{i=0}^{\infty}x^{2i}=\frac{1}{1-x^2}

G_B(x)=\sum_{i=0}^{\infty}x^{5i}=\frac{1}{1-x^5}

G_C(x)=1+x+x^2+x^3+x^4

G_D(x)=1+x

然后四个东西乘起来

G(x)=\frac{1}{1-x^2}*\frac{1}{1-x^5}*(1+x+x^2+x^3+x^4)*(1+x)

}2%$SU9LA]K}{PRHFDL3NN0然后做完了

为了拯救大家的工作量 我们打开mathematica

image

 

那么源问题答案就是f_n=n+1

 

相似例题：BZOJ3028:食物

posted @ 2016-08-23 21:52  zhouyis  阅读(244)  评论(0)  编辑  收藏  举报