最长公共子序列PK最长公共子串

1、先科普下最长公共子序列 & 最长公共子串的区别：

找两个字符串的最长公共子串，这个子串要求在原字符串中是连续的。而最长公共子序列则并不要求连续。

(1)递归方法求最长公共子序列的长度

　　　　1)设有字符串a[0...n]，b[0...m]，下面就是递推公式。

             当数组a和b对应位置字符相同时，则直接求解下一个位置；当不同时取两种情况中的较大数值。

　　　　

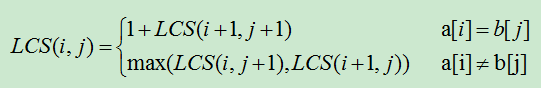
　　　　2)代码如下：

#include<stdio.h>
#include<string.h>
char a[30],b[30];
int lena,lenb;
int LCS(int,int);　　///两个参数分别表示数组a的下标和数组b的下标

int main()
{
    strcpy(a,"ABCBDAB");
    strcpy(b,"BDCABA");
    lena=strlen(a);
    lenb=strlen(b);
    printf("%d\n",LCS(0,0));
    return 0;
}

int LCS(int i,int j)
{
    if(i>=lena || j>=lenb)
        return 0;
    if(a[i]==b[j])
        return 1+LCS(i+1,j+1);
    else
        return LCS(i+1,j)>LCS(i,j+1)? LCS(i+1,j):LCS(i,j+1);
}

用递归的方法优点是编程简单，容易理解。缺点是效率不高，有大量的重复执行递归调用，而且只能求出最大公共子序列的长度，求不出具体的最大公共子序列。

　　(2)动态规划求最长公共子序列的长度

　　　　动态规划采用二维数组来标识中间计算结果，避免重复的计算来提高效率。

　　　　1)最长公共子序列的长度的动态规划方程

　　　　设有字符串a[0...n]，b[0...m]，下面就是递推公式。字符串a对应的是二维数组num的行，字符串b对应的是二维数组num的列。

　　　　

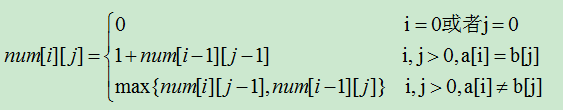
代码如下：

#include<stdio.h>
#include<string.h>

char a[500],b[500];
char num[501][501]; ///记录中间结果的数组
char flag[501][501];    ///标记数组，用于标识下标的走向，构造出公共子序列
void LCS(); ///动态规划求解
void getLCS();    ///采用倒推方式求最长公共子序列

int main()
{
    int i;
    strcpy(a,"ABCBDAB");
    strcpy(b,"BDCABA");
    memset(num,0,sizeof(num));
    memset(flag,0,sizeof(flag));
    LCS();
    printf("%d\n",num[strlen(a)][strlen(b)]);
    getLCS();
    return 0;
}

void LCS()
{
    int i,j;
    for(i=1;i<=strlen(a);i++)
    {
        for(j=1;j<=strlen(b);j++)
        {
            if(a[i-1]==b[j-1])   ///注意这里的下标是i-1与j-1
            {
                num[i][j]=num[i-1][j-1]+1;
                flag[i][j]=1;  ///斜向下标记
            }
            else if(num[i][j-1]>num[i-1][j])
            {
                num[i][j]=num[i][j-1];
                flag[i][j]=2;  ///向右标记
            }
            else
            {
                num[i][j]=num[i-1][j];
                flag[i][j]=3;  ///向下标记
            }
        }
    }
}

void getLCS()
{

    char res[500];
    int i=strlen(a);
    int j=strlen(b);
    int k=0;    ///用于保存结果的数组标志位
    while(i>0 && j>0)
    {
        if(flag[i][j]==1)   ///如果是斜向下标记
        {
            res[k]=a[i-1];
            k++;
            i--;
            j--;
        }
        else if(flag[i][j]==2)  ///如果是斜向右标记
            j--;
        else if(flag[i][j]==3)  ///如果是斜向下标记
            i--;
    }

    for(i=k-1;i>=0;i--)
        printf("%c",res[i]);
}

(3)图示

 

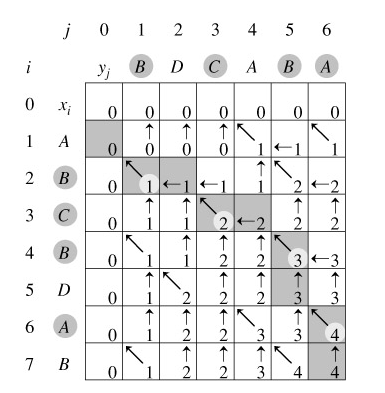
最长公共子串

import java.util.Scanner;

public class Main {
    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        Main mainObj = new Main();
        int len = mainObj.getCommonStrLength(sc.next(),sc.next());
        System.out.println(len);
    }
    
    int getCommonStrLength(String str1, String str2) {
             str1 = str1.toLowerCase();  
            str2 = str2.toLowerCase();  
            int len1 = str1.length();  
            int len2 = str2.length();  
            String min = null;  
            String max = null;  
            String target = null;
            min = len1 <= len2 ? str1 : str2;
            max = len1 >  len2 ? str1 : str2;
            //最外层：min子串的长度，从最大长度开始
            for (int i = min.length(); i >= 1; i--) {
                //遍历长度为i的min子串，从0开始
                for (int j = 0; j <= min.length() - i; j++) {  
                    target = min.substring(j, j + i);  
                    //遍历长度为i的max子串，判断是否与target子串相同，从0开始
                    for (int k = 0; k <= max.length() - i; k++) {  
                        if (max.substring(k,k + i).equals(target)) {  
                            return i;  
                        }
                    }
                }
            }  
            return 0;  
    }
}