编译原理第八次作业
1.设有 NFA M=( {0,1,2,3}, {a,b},0,{3},)其中 f(0,a)={0,1} f(0,b)={0} f(1,b)={2} f(2,b)={3}写出状态转换矩阵,状态转换图
状态转换矩阵：
状态转换图：
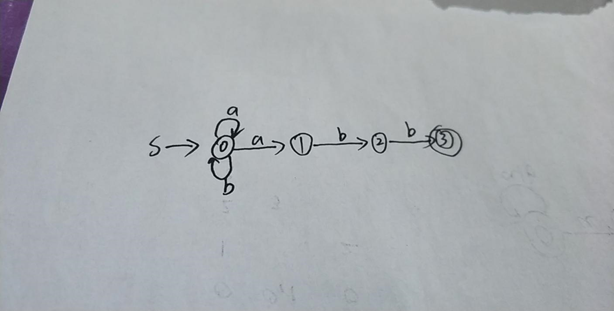
2.NFA 确定化为 DFA
2.1解决多值映射：子集法
（1）. 上述练习1的NFA
状态转换矩阵：
|
|
|
a |
b |
|
A |
0 |
{0,1} |
{0] |
|
B |
{0,1} |
{0,1} |
{0,2} |
|
C |
{0,2} |
{0,1} |
{0,3] |
|
D |
{0,3} |
{0,1} |
{0} |
状态转换图：
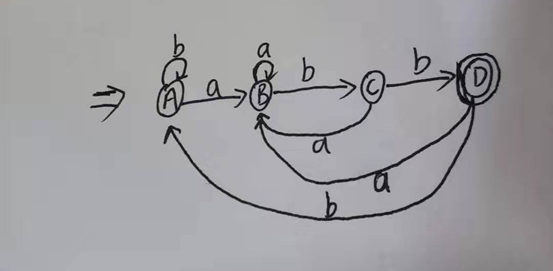
（2）P64页练习3
状态转换矩阵：
|
|
|
0 |
1 |
|
a |
{S} |
{V,Q} |
{U,Q} |
|
b |
{V,Q} |
{Z,V} |
{Q,U} |
|
c |
{Z,V} |
{Z} |
{Z} |
|
d |
{U,Q} |
{V} |
{Z,Q,U} |
|
e |
{Z,Q,U} |
{Z,V} |
{Z,Q,U} |
|
f |
{Z} |
{Z} |
{Z} |
|
g |
{V} |
{Z} |
Ø |
状态转换图：
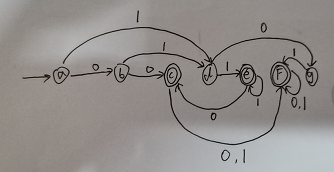
2.2
(1)发给大家的图2
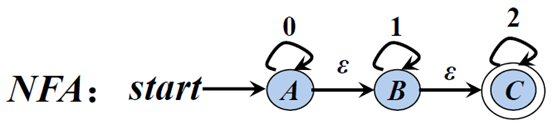
状态转换矩阵：
|
|
|
0 |
1 |
2 |
|
D |
∑{A}=ABC |
∑(A)=ABC |
∑(B)=BC |
∑(C)=C |
|
E |
∑(BC)=BC |
- |
∑(B)=BC |
∑(C)=C |
|
F |
∑(C)=C |
- |
- |
∑(C)=C |
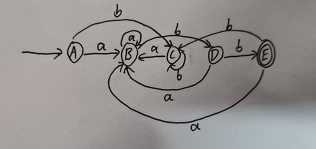
状态转换图：
(2).P50图3.6
状态转换矩阵：
|
|
|
a |
b |
|
A |
ε{0}={0,1,2,4,7} |
ε{3,8}={3,6,7,1,2,4,8} |
ε{5}={5,6,7,1,2,4} |
|
B |
ε{1,2,3,4,6,7,8} |
ε{3,8}={3,6,7,8,1,2,4} |
ε{59}={5,6,7,1,2,4,9} |
|
C |
ε{1,2,4,5,6,7} |
ε{3,8}={3,6,7,8,1,2,4} |
ε{5}={1,2,4,5,6,7} |
|
D |
ε{1,2,4,5,6,7,9} |
ε{3,8}={3,6,7,8,1,2,4} |
ε{5,10}={5,6,7,1,2,4,10} |
|
E |
ε{1,2,4,5,6,7,10} |
ε{3,8}={3,6,7,8,1,2,4} |
ε{5}={1,2,4,5,6,7} |
状态转换图：
