B-Tree算法分析与实现

　　在数据库系统中，或者说在文件系统中，针对存储在磁盘上的数据读取和在内存中是有非常大的区别的，因为内存针对任意在其中的数据是随机访问的，然而从磁盘中读取数据是需要通过机械的方式来读取一个block，不能指定的只读取我们期望的数值，比如文件中的某个int。那么针对存储在磁盘中数据结构的组织就很重要，为了提高访问数据的效率，在多种数据库系统中，采用B-Tree及其变种形式来保存数据，比如B+-Tree。我们这里先主要针对B-Tree的算法进行分析和实现。

　　一、 B-Tree的定义与意义

　　B-Tree的定义是这样的：

　　1、根结点至少有两个子女；

　　2、每个非根节点所包含的关键字个数 j 满足：m/2 - 1 <= j <= m - 1；

　　3、除根结点以外的所有结点（不包括叶子结点）的度数正好是关键字总数加1，故内部子树个数 k 满足：m/2 <= k <= m ；

　　4、所有的叶子结点都位于同一层。

　　根据上诉定义，我们可以看出B-Tree是一个自平衡的树，从第4条可以看出来，1、2、3条主要是规定了B-Tree的节点（Node）分裂（split）的前提一定是满了（overflow）才会进行，而且一定会分裂成数量几乎相同的2个子节点。

　　那么使用B-Tree在数据库中存储数据有什么优势呢？ 我们知道B-Tree是一个扇出（fan-out，也就是可以拥有的子节点数量）不固定的树，和二叉树不同，二叉树的扇出固定只有2，而B-Tree的扇出可以任意大，比如100。扇出非常大，那么在同一个block，或者page中能存放的关键字key也就越多，那么针对文件系统进行数据查找的时候，需要搜索的目录深度也就越少，很简单的算术。二叉树，32层可以存储最多21亿左右的key，100扇出的B-Tree 5层就可以最多存储100亿左右的key！！那么在磁盘中查找数据，或者对数据进行更新时，读取磁盘的次数将大大减少，整体性能有非常非常高的提升。

 

　　二、B-Tree Insert分析实现

　　在了解了B-Tree的定义和意义之后，我们来看下B-Tree insert算法是如何实现的。B-Tree insert算法的描述是这样的：

1、using the SEARCH procedure for M-way trees (described above) find the leaf node to which X should be added.
2、add X to this node in the appropriate place among the values already there. Being a leaf node there are no subtrees to worry about.
3、if there are M-1 or fewer values in the node after adding X, then we are finished.
If there are M nodes after adding X, we say the node has overflowed. To repair this, we split the node into three parts:

Left:
the first (M-1)/2 values
Middle:
the middle value (position 1+((M-1)/2)
Right:
the last (M-1)/2 values

　　简单来说分为3步：

　　1、首先查找需要插入的key在哪个叶节点中

　　2、然后将关键字插入到指定的叶节点中

　　3、如果叶节点没有overflow，那么就结束了，非常简单。如果叶节点overflow了，也就是满了，那么就拆分（split）此节点，将节点中间的关键字放到其父节点中，剩余部分拆分为左右子节点。如果拆分出来放到父节点后，父节点也overflow了，那么继续拆分父节点，父节点当做当前，直到当前节点不再overflow。

　　实现的代码如下：btree.h

　　

#ifndef BTREE_BTREE_H
#define BTREE_BTREE_H

#define NULL 0
#include <algorithm>

// btree节点
struct b_node {
    int num;                // 当前节点key的数量
    int dim;
    int* keys;
    b_node* parent;            // 父节点
    b_node** childs;        // 所有子节点

    b_node() {
    }

    b_node (int _dim) : num(0), parent(NULL) {
        dim = _dim;
        keys = new int[dim + 1];                // 预留一个位置，方便处理节点满了的时候插入操作
        childs = new b_node*[dim + 2];            // 扇出肯定需要比key还多一个
        for (int i=0; i<dim+1; ++i) {
            keys[i] = 0;
            childs[i] = NULL;
        }
        childs[dim+1] = NULL;
    }

    // 返回插入的位置
    int insert(int key) {
        int i = 0;
        keys[num] = key;
        for (i = num; i > 0; --i)
        {
            if (keys[i-1] > keys[i])
            {
                std::swap(keys[i-1], keys[i]);
                continue;
            }
            break;
        }
        ++num;                            // 数量添加
        return i;
    }

    bool is_full() {
        if (num < dim) {
            return false;
        }
        return true;
    }

    // 获取需要插入的位置
    int get_ins_pos(int key) {
        int i = 0;
        for (i=0; i<dim; ++i) {
            if (key > keys[i] && keys[i]) {
                continue;
            }
        }

        return i;
    }
};

// 表达某个值的位置
struct pos {
    b_node* node;            // 所在位置的node指针
    int index;                // 所在node节点的索引
    pos() : node(NULL), index(-1) {
    }
};

class btree {
public:
    btree (int _dim) : dim(_dim), root(NULL) {
    }

    pos query(int key);            // 查找某个某个key
    void insert(int key);        // 插入某个key
    void print();                // 分层打印btree

private:
    pos _query(b_node* root, int key);

    void _print(b_node* node, int level);

    void _insert(b_node* node, int key);
    void _split_node(b_node* node);
    void _link_node(b_node* parent, int pos, b_node* left_child, b_node* right_child);

private:
    int dim;                    // 维度
    b_node* root;                // 根节点
};

#endif

　　所有函数以"_"为开头的，都是内部函数，对外不可见。将针对节点本身的插入操作和基础判断都放在b_node结构中，增加代码的可读性。

　　btree.cpp 代码如下

#include "btree.h"
#include <iostream>
using namespace std;

void btree::insert(int key) {
    _insert(root, key);
}

void btree::_insert(b_node* node, int key) {

    // 根节点为空
    if (root == NULL)
    {
        root = new b_node(dim);
        root->insert(key);
        return;
    }
    
    int index = node->num;
    while (index > 0 && node->keys[index-1] > key)                // 找到对应的子节点
    {
        --index;
    }
    
    // 如果当前node插入节点已经没有左右儿子了，那么就在当前节点中插入
    if (!node->childs[index])                    // 因为btree一定是既有左儿子，又有右儿子，所以只判断其中一个是否存在就可以了
    {
        // 如果节点没有满
        if (!node->is_full())
        {
            node->insert(key);
            return;
        }

        // 如果当前节点已经满了，需要将中间节点拆分，然后加入到父节点中，将剩余的2个部分，作为新节点的左右子节点
        // 如果父节点加入新的key之后也满了，那么递归上一个步骤
        node->insert(key);
        _split_node(node);
        return;
    }

    // 已经遍历到最右key了
    if (index == node->num)
    {
        _insert(node->childs[index], key);
        return;
    }

    _insert(node->childs[index], key);
    return;
}

void btree::_split_node(b_node* node) {
    if (!node || !node->is_full()) {
        return;
    }

    int split_pos = (node->dim-2)/2 + 1;                // 分割点
    int split_value = node->keys[split_pos];
    b_node* split_left_node = new b_node(dim);
    b_node* split_right_node = new b_node(dim);
    
    // 处理左儿子节点
    int i = 0;
    int j = 0;
    for (; i<split_pos; ++i, ++j) {
        split_left_node->keys[i] = node->keys[j];
        split_left_node->childs[i] = node->childs[j];
    }
    split_left_node->childs[i] = node->childs[j];
    split_left_node->num = split_pos;

    // 处理右儿子节点
    for (i = 0, j=split_pos+1; i < dim - split_pos; ++i, ++j) {
        split_right_node->keys[i] = node->keys[j];
        split_right_node->childs[i] = node->childs[j];
    }
    split_right_node->childs[i] = node->childs[j];
    split_right_node->num = dim - split_pos;

    // 将分割的节点上升到父节点中
    b_node* parent = node->parent;
    if (!parent) {            // 父节点不存在
        b_node* new_parent = new b_node(dim);
        new_parent->insert(split_value);

        _link_node(new_parent, 0, split_left_node, split_right_node);

        // 重置根节点
        root = new_parent;    
        return;
    }

    // 如果父节点也满了，那么先将split出来的节点加入父节点，然后再对父节点split
    if (parent->is_full()) {
        int new_pos = parent->insert(split_value);

        _link_node(parent, new_pos, split_left_node, split_right_node);
        _split_node(parent);                    // 如果父节点也满了， 那么继续split父节点
    }
    else {
        int pos = parent->insert(split_value);
        _link_node(parent, pos, split_left_node, split_right_node);
    }

    return;
}

void btree::_link_node(b_node* parent, int pos, b_node* left_child, b_node* right_child) {
    parent->childs[pos] = left_child;
    left_child->parent = parent;

    parent->childs[pos+1] = right_child;
    right_child->parent = parent;
}

void btree::print() {
    cout << "==================================" << endl;
    _print(root, 1);
    cout << "==================================" << endl;
}

void btree::_print(b_node* node, int level) {
    if (!node) {
        return;
    }

    cout << level << ":";
    for (int i=0; i<node->num; ++i)    {
        cout << node->keys[i] << ",";
    }
    cout << endl;

    for (int i=0; i<node->num+1; ++i) {
        _print(node->childs[i], level+1);
    }
    return;
}

　　（1） insert接口调用内部的_insert函数。

　　（2） _insert中首先判断B-Tree是否为空，要是空的话，先创建根节点，然后简单的将key插入就可以了。

　　（3）如果不是空的话，判断key在当前节点是否可以插入，如果当前节点就是叶子节点，那么肯定是没有子节点了，也就是childs是空了。如果不是叶子节点，那么就需要递归下层子节点做判断，直到直到可以插入的叶子节点，然后做插入操作。

　　（4）插入的时候先判断当前节点是否已经满了，如果没有满，那么就简单的直接插入，调用b_node的insert就结束了。否则先将key插入，然后_split_node针对节点进行分裂。

　　（5）在_split_node中，先找到需要上升到父节点的key，然后将key左边的所有key变成左子树，将key右边的所有key变成右子树，对里面的key和子节点指针做复制。然后将split_value添加到父节点中，没有父节点就先创建一个父节点，有就加入。如果父节点也overflow了，就递归的进行_split_node，直到当前节点没有overflow为止。

　　代码中的dim是维度的意思，维度为3，就是指fan-out为4，也就是一个node可以保持3个key，拥有最多4个子节点。这个概念可能不同的地方略有差异，需要根据实际的说明注意一下。

　　测试代码：

#include "btree.h"

int main() {
    btree btr(3);
    
    btr.insert(10);
    btr.insert(12);
    btr.insert(50);
    btr.insert(11);
    btr.print();

    btr.insert(20);
    btr.insert(22);
    btr.print();

    btr.insert(33);
    btr.insert(35);
    btr.print();

    btr.insert(40);
    btr.print();

    btr.insert(42);
    btr.print();

    btr.insert(13);
    btr.insert(1);
    btr.insert(23);
    btr.print();
    return 0;
}

　　

　　三、BTree删除

　　BTree删除的算法，比插入还要稍微的复杂一点。通常的做法是，当删除一个key的时候，如果被删除的key不在叶子节点中，那么我们使用其最大左子树的key来替代它，交换值，然后在最大左子树中删除。

　　

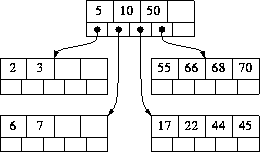
　　以上图为例，如果需要删除10，那么我们使用7和10进行交换，然后原来的[6,7]变成[6,10]，删除10.

从BTree中删除key就可以保证一定是在叶子节点中进行的了。删除主要分为2步操作：

　　1、将key从当前节点删除，由于一定是在叶子节点中，那么根本不需要考虑左右子树的问题。

　　2、由于从节点中删除了key，那么节点中key的数量肯定减少了。如果节点中key的数量小于(M-1)/2了，我们就认为其underflowed了。如果underflowed没有发生，那么这次删除操作就简单的结束了，如果发生了，那么就需要修复这种问题（这是由于BTree的自平衡特性决定的，可以回头看下一开始说的BTree定义）。

　　针对BTree的删除，复杂的部分就是修复underflowed的问题。如何修复这种问题呢？做法是从被删除节点的邻居“借”key来修复，那么一个节点可能有2个邻居，我们选择key数量更多的邻居来“借”。那么借完之后，我们将被删除节点，其邻居，以及其父节点中key来生成一个新的node，“combined node”（连接节点）。生成新的节点之后，如果其数量大于（M-1），或者等于（M-1）的做法是不一样的，分为2中做法。

　　（1）如果大于（M-1），那么处理方法也比较简单，将新的combined node分裂成3个部分，Left，Middle，Right，Middle就是combined node正中间的key，用来替代原来的父节点值，Left和Right作为新的左右子树。由于大于（M-1），那么可以保证新的Left和Right都是满足BTree要求的。

　　（2）如果等于（M-1）就比较复杂了。由于新的Combined node的节点数量刚好满足BTree要求，而且也不能像（1）的情况那样进行分裂，那么就等于新节点从父节点“借”了一个值，如果父节点被借了值之后，数量大于等于（M-1）/2，那么没问题，修复结束。如果父节点的值也小于(M-1)/2了，那么就需要再修复父节点，重复这个步骤，直到根节点为止。

　　比如上面的树，删除key=3，那么删除后的树为

　　

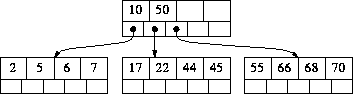
　　由于BTree根节点的特殊性，它只需要最少有一个节点就可以了，如果修复到根节点还有至少一个节点，那么修复结束，否则删除现有根节点，使用其左子树替代，左子树可能为空，那么整棵BTree就是空了！

　　代码如下：

　

void btree::del(int key) {
    _del(root, key);
}

void btree::_del(b_node* node, int key) {
    // 先找到删除节点所在的位置
    pos p = query(key);

    // 查找其最大左子树key
    pos left_max_p = _get_left_max_key(key);

    b_node* del_node = p.node;
    if (left_max_p.node != NULL)
    {
        del_node = left_max_p.node;
        std::swap(p.node->keys[p.index], left_max_p.node->keys[left_max_p.index]);    // 将最大左子树key和当前key进行交换
    }

    // 现在针对key进行删除
    del_node->del(key);    

    // 先判断如果没有underflowed，就直接结束了
    if (!del_node->is_underflowed()) {
        return;
    }

    _merge_node(del_node);
}

void btree::_merge_node(b_node* del_node) {
    // 如果underflowed了，那么先判断是否为根节点，根节点只要最少有一个key就可以了，其他非根节点最少要有(M-1)/2个key
    if (del_node->is_root())
    {
        if (del_node->num == 0)                // 根节点已经没有key了
        {
            root = del_node->childs[0];
        }
        return;
    }

    // 如果是叶子节点并且underflowed了，那么就需要从其“邻居”来“借”了
    b_node* ngb_node = del_node->get_pop_ngb();
    if (ngb_node == NULL)
    {
        return;
    }

    int p_key_pos = (del_node->pos_in_parent + ngb_node->pos_in_parent) / 2;
    int parent_key = del_node->parent->keys[p_key_pos];

    // 处理组合后的节点
    b_node* combined_node = new b_node(del_node->num + 1 + ngb_node->num);

    if (del_node->pos_in_parent < ngb_node->pos_in_parent)
    {
        int combined_n = 0;
        _realloc(combined_node, del_node, del_node->num);
        combined_n += del_node->num;

        combined_node->insert(parent_key); ++combined_n;

        _realloc(combined_node, ngb_node, ngb_node->num, combined_n);
    }
    else
    {
        int combined_n = 0;
        _realloc(combined_node, ngb_node, ngb_node->num);
        combined_n += ngb_node->num;

        combined_node->insert(parent_key); ++combined_n;

        _realloc(combined_node, del_node, del_node->num, combined_n);
    }


    // 如果邻居key的数量大于(M-1)/2, 那么执行case1逻辑，将combined后的node中间值和parent中的值进行交换，然后分裂成2个节点
    if (ngb_node->num > dim/2)
    {
        int split_pos = (del_node->num + ngb_node->num + 1) / 2;
        b_node* combined_left = new b_node(dim);
        b_node* combined_right = new b_node(dim);

        _realloc(combined_left, combined_node, split_pos);
        _realloc(combined_right, combined_node, combined_node->num - split_pos - 1, 0, split_pos + 1);

        combined_left->parent = del_node->parent;
        combined_right->parent = del_node->parent;

        b_node* parent = del_node->parent;
        std::swap(combined_node->keys[split_pos], del_node->parent->keys[del_node->pos_in_parent]);
        parent->childs[p_key_pos] = combined_left;
        combined_left->pos_in_parent = p_key_pos;
        parent->childs[p_key_pos + 1] = combined_right;
        combined_right->pos_in_parent = p_key_pos + 1;
        
        return;
    }

    // 如果邻居的key的数量刚好是(M-1)/2，那么合并之后就可能会发生underflowed情况
    // 邻居key的数量不可能会发生小于(M-1)/2的，因为如果是这样，之前就已经做过fix处理了
    del_node->parent->del(parent_key);
    del_node->parent->childs[del_node->pos_in_parent] = combined_node;
    combined_node->parent = del_node->parent;
    combined_node->pos_in_parent = del_node->pos_in_parent;

    // 如果parent去掉一个节点之后并没有underflowed，那么就结束
    if (!del_node->parent->is_underflowed())
    {
        return;
    }

    // 否则继续对parent节点进行修复, 直到根节点
    _merge_node(del_node->parent);
    return;
}

void btree::_realloc(b_node* new_node, b_node* old_node, int num, int new_offset, int old_offset) {
    int i = old_offset;
    int n = new_offset;
    for (; i<old_offset + num; ++i, ++n)
    {
        new_node->keys[n] = old_node->keys[i];
        new_node->childs[n] = old_node->childs[i];

        if (new_node->childs[n]) {
            new_node->childs[n]->parent = new_node;
            new_node->childs[n]->pos_in_parent = n;
        }
    }
    new_node->childs[n] = old_node->childs[i];
    if (new_node->childs[n]) {
        new_node->childs[n]->parent = new_node;
        new_node->childs[n]->pos_in_parent = n;
    }
    new_node->num += num;
    return;
}

 

　　

　　测试代码通过一个个的值插入，我们有意的数值安排，将我们的B-Tree从1层，最后扩展到了3层，可以通过print接口来更方便的观看一下B-Tree各层的数值。

　　如果想知道自己实现的是否正确，或者想了解B-Tree插入节点的流程，https://www.cs.usfca.edu/~galles/visualization/BTree.html 这个网址用动画的方式给我们展示B-Tree的插入和分裂过程，非常形象，很好理解。