浅尝 ECDHE 协议流程
前言
ECDHE 我之前是听都没听过, 但是新业务需要对前后端通信进行加密, 经过大佬推荐才知道有这个东西, 经过几天的学习和踩坑😇, 才大致明白其流程和使用方式.
过程坎坷, 好在最后还是成功运用到了业务中, 大大提高了业务的安全性. 👍
这里记录一下本人对 ECDHE 的理解和注意要点
ECDHE
椭圆曲线迪菲-赫尔曼金钥交换 - 维基百科,自由的百科全书 (wikipedia.org)
我们先来说说 ECDH, ECDH(Elliptic Curve Diffie–Hellman key exchange) 是一种密钥协商协议, 其精髓是通过椭圆曲线算法(ECC), 让客户端和服务端不传输私钥(需要传输公钥), 就可以计算出一样的结果(共有加密资料), 即使协商过程被第三方(中间人)知晓和监听, 也不会泄露密钥.
而 ECDHE(ECDH Ephemeral) 与 ECDH 无本质差别, 他们协商的流程一模一样, 只是ECDHE代表协商出的共有加密资料是临时的, 就算当前的加密资料泄露, 也不会影响其之前的历史数据被解密, 这是使用方式决定的, 大白话意思就是, 我们通过 ECDH 生成的共有加密数据有实效性, 会通过逻辑在一段时间或特定事件后重新协商, 而不是只协商一次, 如果只协商一次, 如果共有加密资料被泄露, 则之前的所有数据都可以解开. 这种共有加密数据资料泄露也不会对历史数据有影响的特性在密码学中被称为 前向安全性.
椭圆曲线密码学(ECC)
ECC 是 ECDH 的核心
椭圆曲线密码学 - 维基百科,自由的百科全书 (wikipedia.org)
JavaScript ECDH Key Exchange Demo (stanford.edu)
椭圆曲线算法(ECC) 是一种基于椭圆曲线数学的公开密钥加密算法, ECC 相比于 RSA 来讲, 有更短的密钥长度和相同等级的安全性(ECC被广泛认为是在给定密钥长度的情况下,最强大的非对称算法,因此在对带宽要求十分紧的连接中会十分有用.)
而且, ECC可以定义群之间的双线性映射, 即通过两个向量空间上的元素, 生成第三个向量空间上的元素的函数. 这使得他可以让两对数据通过交换和计算得出相同结果
ECC 算法衍生出了一些加密协议, 常见的有 ECDHE, MQV, ECDSA 等
- ECC 的公钥其实对应了椭圆曲线数学的 XY 坐标, 根据种子随机生成
- ECC 的私钥对应了椭圆曲线数学的 a 参数, 与公钥对应
- ECC 计算出的 share 也是 XY 坐标
- ECC 的种子有公开的几个, 例如
secp128r1/secp256r1/secp192k1等, 两端的种子需要保持一致.
在线 ECDH 可参照 JavaScript ECDH Key Exchange Demo (stanford.edu)
椭圆曲线数学
椭圆曲线的数学原理在这里
椭圆曲线 - 维基百科,自由的百科全书 (wikipedia.org)
常言道, 学好数理化, 走遍天下都不怕. 可惜我是宅男, 不爱出门💀
这个原理在我的理解范畴之外了, 如果你对数学有兴趣, 可以尝试了解
三者关系
先诞生出的椭圆曲线数学公式, 而后有的基于椭圆曲线数学公式的密码学算法 ECC, 而ECC 又衍生出一些加密协议和协议, ECDH就是其中一种
破解概率
直接引用 wiki 原文
如果攻击者拥有大型量子计算机,那么他可以使用秀尔算法解决离散对数问题,从而破解私钥和共享秘密。目前的估算认为:破解256位素数域上的椭圆曲线,需要2330个量子比特与1260亿个托佛利门。相比之下,使用秀尔算法破解2048位的RSA则需要4098个量子比特与5.2万亿个托佛利门。因此,椭圆曲线会更先遭到量子计算机的破解。目前还不存在建造如此大型量子计算机的科学技术,因此椭圆曲线密码学至少在未来十年(或更久)依然是安全的。但是密码学家已经积极展开了后量子密码学的研究。其中,超奇异椭圆曲线同源密钥交换(SIDH)有望取代当前的常规椭圆曲线密钥交换(ECDH)
ECDH 协商流程
前面说过, ECDHE 和 ECDH 不同是协商出的密钥有效期, 实际上协商流程是一致的, 所以这里严谨一点, 就叫 ECDH 协商流程
ECDH 本身的协商流程如下图所示(按照数字编号走流程):

上面说过, ECDH实际上是协商共享加密数据的过程, 难点在 ECC 的本身实现, 而交换的过程很简单, 互相发送自己生成的公钥即可, 公钥其实就是椭圆算法中的计算所需的 X/Y 坐标.
安全性
中间人只监听数据
两端协商密钥的过程中, 均未传输自己的私钥.
这样, 即使有中间人监听了两端之间的网络数据, 也只能获取到两端的公钥, 无法计算出真正的 shareX/shareY , 如图所示:
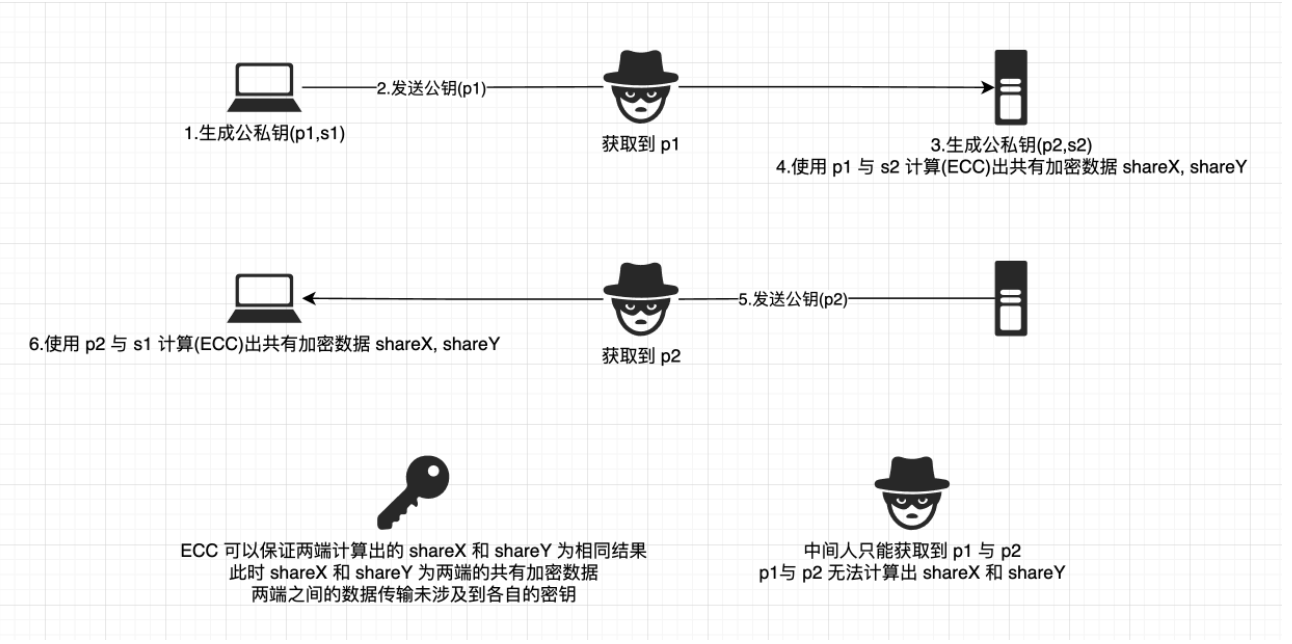
中间人监听并伪造客户端和服务端
如果中间人能做到, 同时伪造成客户端和服务端(对于客户端来讲是服务端, 对于服务端来讲是客户端), 那么ECDH生成的共享加密数据, 客户端与服务端无法对应
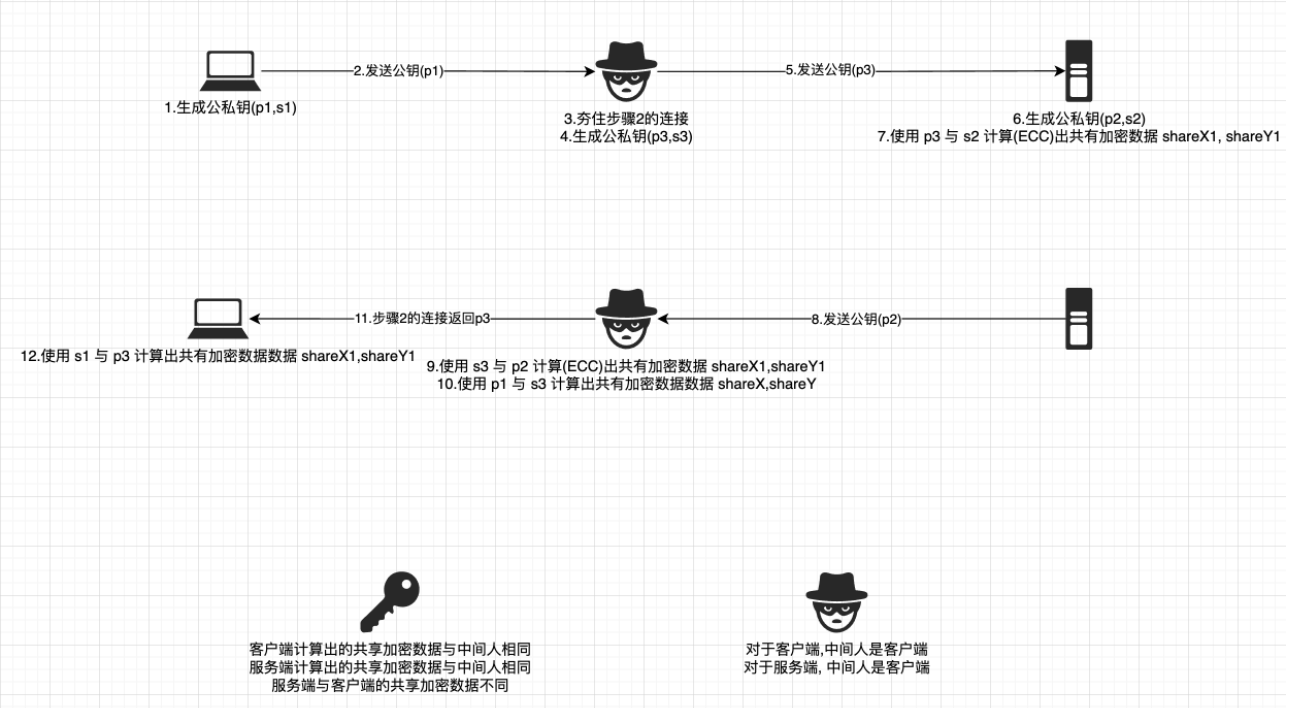
但是细想, 这时候, 虽然客户端与服务端的共享加密数据不相同, 但是ECDH只是一个协商密钥的过程, 中间人在此种情况下成功在客户端与服务端不知情的情况下正常走完了协商流程, 之后的加密数据, 如果使用了这个协商出的加密数据, 就会导致之后的数据被中间人截获/解析, 并且无感知, 例如:
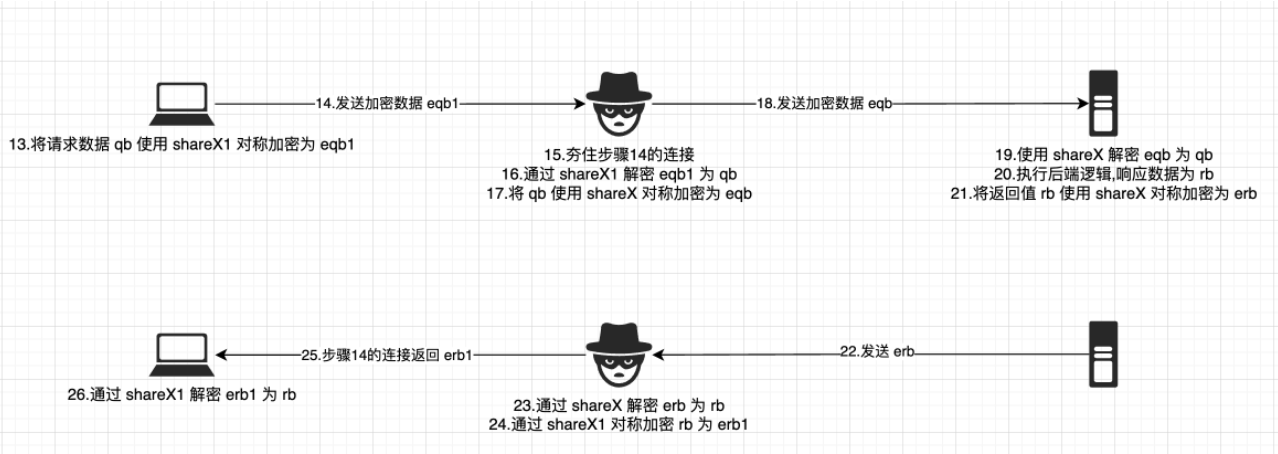
不过, 这就逃脱了 ECDH 的范畴了, 这是真正需要开发者在业务中考虑的事情.
ECDH在 TLS1.2 中的使用流程
TLS1.2 的详细立案可看:
RFC 5246: The Transport Layer Security (TLS) Protocol Version 1.2 (rfc-editor.org)
在 TLS1.2 协议中, 就使用了 ECDHE 来交换密钥, 我们来分析一下 TLS1.2 怎么使用 ECDHE 的:
TLS v1.2 handshake overview | by apoorv munshi | Medium
如文章所述, 在步骤 Server Key Exchange & Server Hello Done 时, 服务端不止返回了自己的 ECC 公钥, 还使用了 TLS 证书生成时的私钥对信息进行了签名(RSA), 而后, 客户端在接受到信息后, 尝试使用 TLS 证书中的公钥对信息进行验签, 用来保证数据一定是服务端返回的, 解决中间人篡改问题, 如图:

业务中使用 ECDHE 进行前后端通信数据加密
我们可以仿造 TLS1.2 协议来打造一个前后端通信加密的流程, 但是需要注意以下几点:
- ECDH 本身的协商过程是"明文的", 协商出共享加密数据后使用该数据对 body 进行加密传输才是"安全的"
- ECDH 变成 ECDHE 是加了时效性, 因此共享加密数据的淘汰策略很重要
- ECC 生成的公私钥实际上是 XY 坐标, 考虑前端 JS 出问题生成 XY 重复的可能
修改后的密钥协商流程如下:
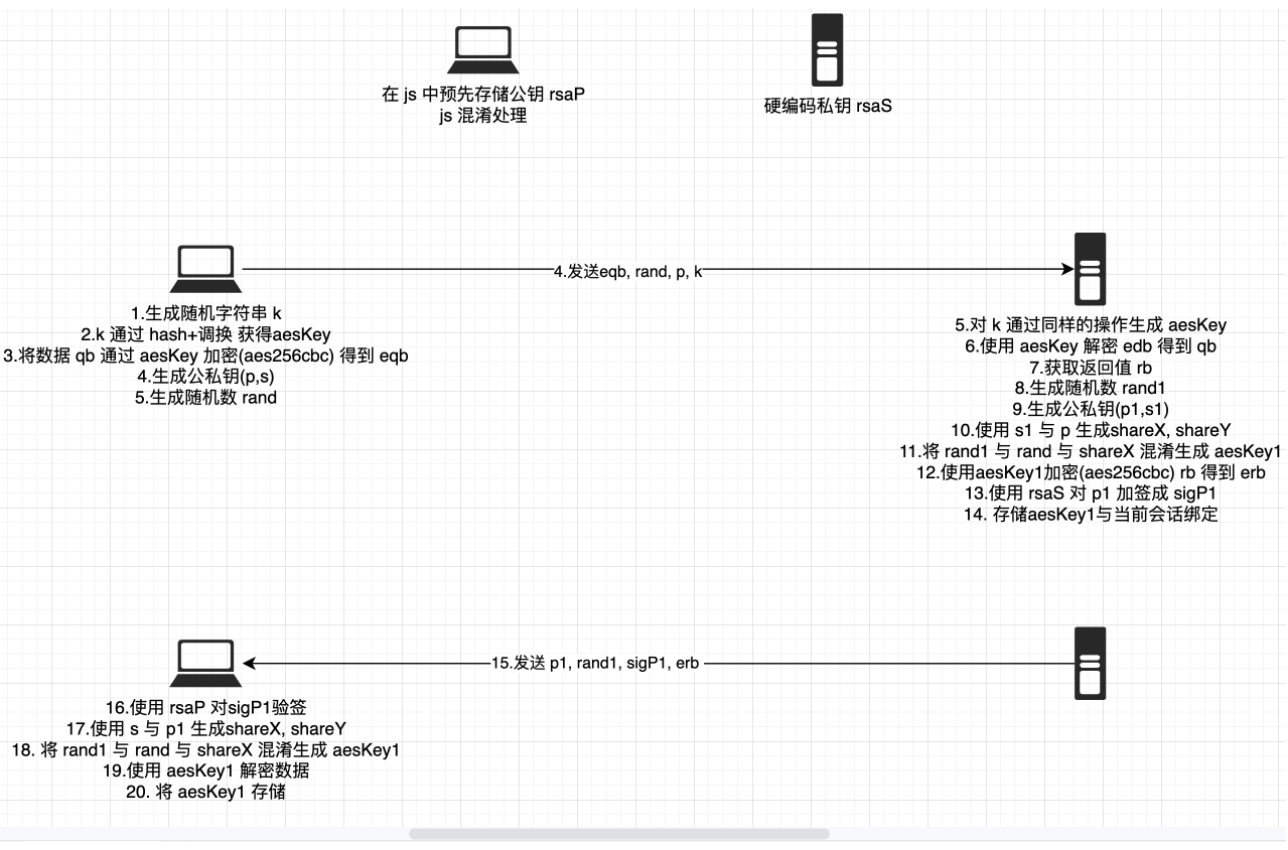
之后的请求, 均使用aesKey1进行aes256cbc加解密通信

针对问题1, 我们使用混淆生成 key 进行 aes 加密的方式, 对请求进行加密, 提高解密难度
针对问题2, 我们将单次协商的共享密钥与当前会话和用户设备绑定, 并对会话进行有效期淘汰管理, 当触发到淘汰标准时会将服务端密钥进行删除, 客户端需重新协商密钥才可重新通信
针对问题3, 我们在前后端加入随机数生成并于最终的 shareX 混淆, 防止ECC生成公私钥时因实现问题导致的重复密钥


 浙公网安备 33010602011771号
浙公网安备 33010602011771号