什么是像素化
学计算机的人往往都比较清楚图形和图像的区别,而且往往能够从数据结构的角度理解这两者的区别,一般来说,图形是由几何空间中的基本图元所组成,表现为用外部轮廓线条勾勒成的矢量图。例如由计算机绘制的直线、圆、矩形、曲线、图表等。而图像是由扫描仪、摄像机等输入设备捕捉实际的画面产生的数字图像,是由像素点阵构成的位图。例如在二维几何空间中,同样是为了表述一个四边形,从图形的角度去看,需要提供四个顶点的坐标作为基本图元,然后提供一个画线的指令,将四个顶点按顺序提供出来。而从图像的角度看,一个四边形需要映射为一个特定分辨率位图上的像素集合。例如一张大小为9*9的位图上,四边形的边所在的像素集被涂为与背景不用的颜色,用以表述这个形状。

像素化、以及体素化的过程是图形转变为图像的一个过程,在一些场合被称作离散化(discretization),而其逆向过程,即由图像生成图形的过程可以被称作轮廓生成(2D)或者表面生成(3D)。在之前的博客介绍了几种从三维图像生成表面的算法,它们就属于从图像到图形的表面生成算法范畴。而这篇文章主要介绍一下二维空间像素化的方法,同时为引申到三维空间做准备。下表显示了这几种概念和相应算法之间的关系:
| 图像到图形 | 图形到图像 | |
| 二维 | 轮廓生成:MarchingSquares算法等 | 像素化算法 |
| 三维 | 表面生成:Marchingcubes算法,Cuberille算法等 | 体素化算法 |
而下面的图片也形象的说明了图像与图形的区别,同样的箭头,在不同的表示下是不同的形式。事实上计算机内部无时无刻不在进行这样的转换,通常人们大脑中习惯按几何方式去理解图形,但用屏幕显示他们时,计算机需要将其转为像素点阵的模式。
 |
 |
 |
| 图形 | 图形映射图像的像素 | 生成图像 |
基本图元的像素化—线段的像素化
任意二维形状像素化的基础是基本图元的像素化,二维空间的基本图元就是点和线段。不难知道,对任意几何点P(X,Y)的像素化即是在给定分辨率下寻找到P的对应像素点,像素点也可以理解为二维空间中的格子,P落在哪个格子上,该格子即是P对应的像素。P(345.6,233.1)在512*512的位图上,可以将像素(346,223)作为P的近似来表示P。关键的算法是线段的像素化,有一定计算机图形学或者图像处理基础的人应该都听说过DrawLine算法,这个算法就是一种线段像素化的手段。在Windows画图中画过下图的这种细线段的人应该知道这样的像素化的线段。
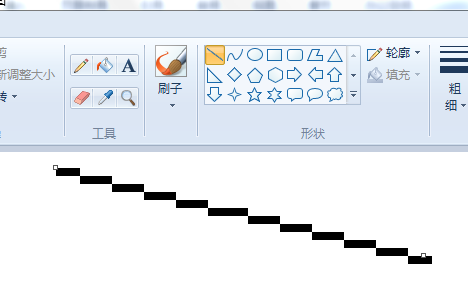
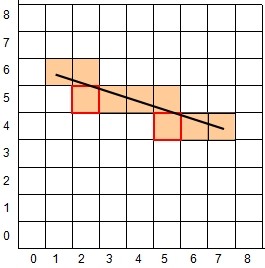
这种线段又被称作Bresenham线,是线段像素化的一种,可以用来渲染线段,事实上,还有一种SuperCover线,同样能够用来表征线段像素化的结果,不过其跟Bresenham线有所不同,细节从下图对比中可以看出,若画线段AB,Bresenham线只要求从A到B有着8向联通关系最细像素组合;而SuperCover线要求像素组合是AB所穿过的所有像素。不难看出,SuperCover线的像素集包含Bresenham线的像素集。
 |
 |
 |
| Bresenham线 | SuperCover线 | 同一张图对比,引自Eugen Dedu,ThisAlg指的就是SuperCover |
下面提供两种画Bresenham线的方法,一种是使用简单的DDA算法,一种是使用Bresenham算法。为此特意声明一个ByteMatrix类型用来表示8位图结构,对外提供获取像素值和设置像素值的接口,所有的像素化算法都在此结构上进行,每一个位图结构初始化为0,涂色操作是将其修改为255。其代码如下:
class ByteMatrix { public: int width; int height; ByteMatrix(int width,int height,byte value) { this->width=width; this->height=height; this->data=new byte[width*height]; memset(data,0,width*height); } ~ByteMatrix() { delete[] data; } inline void SetValue(int x,int y, byte v) { data[x+width*y]=v; } inline byte GetValue(int x,int y) { return data[x+width*y]; } void SaveRaw(const char* fileName) { FILE *const nfile = fopen(fileName,"wb"); fwrite(data,sizeof(unsigned char),width*height,nfile); fclose(nfile); return; } private: byte* data; };
算法1—DDA法
DDA法利用了Bresenham线的一个性质,即在线拥有最长投影的那个轴上,选择任意整数点作为自变量,Bresenham线上拥有其唯一对应的像素点。
 |
| 在横轴方向上每个X有唯一方块对应,而Y方向上不唯一 |
这样DDA算法可以采用这样的思路实现:对从A(X0,Y0)到B(X1,Y1)的线段,寻找投影最长的一个轴,然后从此轴上的最小值开始,依次使用直线方程计算出Y的位置,然后将离此位置最近的像素涂色。代码如下所示(其中Trunc函数是四舍五入函数,实现方式是+0.5取整):
static void DrawLine_DDA(ByteMatrix& bmp,Point2d p0,Point2d p1) { int dx=p1.X-p0.X; int dy=p1.Y-p0.Y; if(abs(dx)>abs(dy)) { if(p0.X>p1.X) { Point2d temp=p1; p1=p0; p0=temp; } for(int i=p0.X;i<=p1.X;i++) { float y=dy*(i-p0.X)/dx+p0.Y; bmp.SetValue(i,Trunc(y),255); } } else { if(p0.Y>p1.Y) { Point2d temp=p1; p1=p0; p0=temp; } for(int i=p0.Y;i<=p1.Y;i++) { float x=dx*(i-p0.Y)/dy+p0.X; bmp.SetValue(Trunc(x),i,255); } } }
算法2—Bresenham算法
Bresenham算法是DDA算法画线算法的一种改进算法。本质上它也是采取了步进的思想。不过它比DDA算法作了优化,避免了步进时浮点数运算,同时为选取符合直线方程的点提供了一个好思路。首先通过直线的斜率确定了在x方向进行单位步进还是y方向进行单位步进:当斜率k的绝对值|k|<1时,在x方向进行单位步进;当斜率k的绝对值|k|>1时,在y方向进行单位步进。http://blog.csdn.net/clever101/article/details/6076841详细介绍了这一算法,网上也能找到特别多关于这个算法的实现和思路讲解,所以这里就不多重复。这里贴上一份代码:
static void DrawLine_Bresenham(ByteMatrix& bmp,Point2d p0,Point2d p1) { int y1=p0.Y; int x1=p0.X; int y2=p1.Y; int x2=p1.X; const bool steep = (abs(y2 - y1) > abs(x2 - x1)); if(steep) { std::swap(x1, y1); std::swap(x2, y2); } if(x1 > x2) { std::swap(x1, x2); std::swap(y1, y2); } const float dx = x2 - x1; const float dy = abs(y2 - y1); float error = dx / 2.0f; const int ystep = (y1 < y2) ? 1 : -1; int y = (int)y1; const int maxX = (int)x2; for(int x=(int)x1; x<maxX; x++) { if(steep) { bmp.SetValue(y,x, 255); } else { bmp.SetValue(x,y, 255); } error -= dy; if(error < 0) { y += ystep; error += dx; } } }
关于画SuperCover线的方法,网上的资料就不如Bresenham线多了,毕竟这条线比起Bresenham线,画的像素更多,因此在渲染线段上面不如Bresenham线简单高效。但SuperCover线也有不少其他方面的用途,所以这里也简单的叙述一下实现SuperCover线画法的算法。
算法3—像素求交法
根据SuperCover线的定义,该线的所有像素都必须被线段穿过。若将像素想象成方块的形状,位图想象成网格图,线段与这些网格相交,不难分析出交点要么是在平行与X的格线上,要么是在平行Y的格线上。假如线段AB的X范围为X0~X1,Y范围是Y0~Y1,那所有在X0~X1范围的所有垂直X轴的格线都能与线段AB有交点,同理Y0~Y1范围的所有垂直于Y轴的格线也有交点,而且不难知道,AB在哪个轴投影更长,则垂直于哪个轴的格线与AB的交点则更多。因此一个简单的画SuperCover线的思路是:先找出投影长的那一维,不妨假设是X轴投影更长,则求出X0-~X1所有垂直X轴格线与AB的交点,例如下图所示的交点:
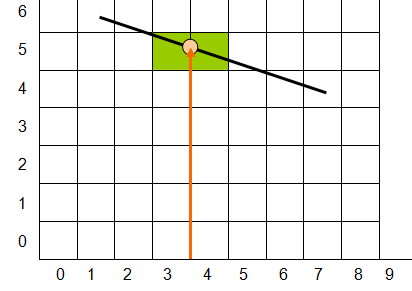
每一个交点都能对应找到两个和它相邻的像素(绿色标注)。这样,每一个交点都找出两个关联像素并涂色后,就实现了SuperCover线的绘制。实现的代码如下:
static void DrawSuperCoverLine_Simple(ByteMatrix& bmp,Point2d p0,Point2d p1) { int dx=p1.X-p0.X; int dy=p1.Y-p0.Y; if(abs(dx)>abs(dy)) { if(p0.X>p1.X) { Point2d temp=p1; p1=p0; p0=temp; } for(float i=p0.X+0.5f;i<=p1.X;i+=1.0f) { float y=dy*(i-p0.X)/dx+p0.Y; bmp.SetValue((int)(i-0.5f),Trunc(y),255); bmp.SetValue((int)(i+0.5f),Trunc(y),255); } } else { if(p0.Y>p1.Y) { Point2d temp=p1; p1=p0; p0=temp; } for(float i=p0.Y+0.5f;i<=p1.Y;i+=1.0f) { float x=dx*(i-p0.Y)/dy+p0.X; bmp.SetValue(Trunc(x),(int)(i-0.5f),255); bmp.SetValue(Trunc(x),(int)(i+0.5f),255); } } }
算法4—基于Bresenham的改进方法
上面那个算法其实是作者自己想的直接了当的算法,自然比不上专业的高效的算法。Eugen Dedu在他的网页上谈到了一种通过修改Bresenham算法的代码来实现画SuperCover线的算法。在网页http://lifc.univ-fcomte.fr/~dedu/projects/bresenham/index.html上他详细的提出了自己的思路,这个思路简单的说就是:Bresenham算法不是一步一步的从A到B涂色吗?那么在每一次涂色时注意一下是往那个像素涂色的,Y方向有没有变化,如果有,就计算一下这个线是偏向那个方向,顺便把那个方向的角落也给填上。例如下图所示的:Bresenham算法若从A画到B,一般来说不会正好经过AB交点的那个像素,根据直线的斜率应该是会向上或下有个偏移,那么根据这个偏移,把D或者C填上即可。详情可以看他链接里的内容,说的比较详细,这里就不重复了。顺便把他的代码贴这:
static void DrawSuperCoverLine_Bresenham(ByteMatrix& bmp,Point2d p0,Point2d p1) { int y1=p0.Y; int x1=p0.X; int y2=p1.Y; int x2=p1.X; int i; // loop counter int ystep, xstep; // the step on y and x axis int error; // the error accumulated during the increment int errorprev; // *vision the previous value of the error variable int y = y1, x = x1; // the line points int ddy, ddx; // compulsory variables: the double values of dy and dx int dx = x2 - x1; int dy = y2 - y1; bmp.SetValue(x1, y1,255); // first point // NB the last point can't be here, because of its previous point (which has to be verified) if (dy < 0){ ystep = -1; dy = -dy; }else ystep = 1; if (dx < 0){ xstep = -1; dx = -dx; }else xstep = 1; ddy = 2 * dy; // work with double values for full precision ddx = 2 * dx; if (ddx >= ddy){ // first octant (0 <= slope <= 1) // compulsory initialization (even for errorprev, needed when dx==dy) errorprev = error = dx; // start in the middle of the square for (i=0 ; i < dx ; i++){ // do not use the first point (already done) x += xstep; error += ddy; if (error > ddx){ // increment y if AFTER the middle ( > ) y += ystep; error -= ddx; // three cases (octant == right->right-top for directions below): if (error + errorprev < ddx) // bottom square also bmp.SetValue(x,y-ystep,255); else if (error + errorprev > ddx) // left square also bmp.SetValue(x-xstep,y ,255); else{ // corner: bottom and left squares also bmp.SetValue(x,y-ystep,255); bmp.SetValue(x-xstep,y,255); } } bmp.SetValue(x,y,255); errorprev = error; } }else{ // the same as above errorprev = error = dy; for (i=0 ; i < dy ; i++){ y += ystep; error += ddx; if (error > ddy){ x += xstep; error -= ddy; if (error + errorprev < ddy) bmp.SetValue(x-xstep,y,255); else if (error + errorprev > ddy) bmp.SetValue(x,y-ystep,255); else{ bmp.SetValue( x-xstep,y,255); bmp.SetValue( x,y-ystep,255); } } bmp.SetValue( x,y,255); errorprev = error; } } // assert ((y == y2) && (x == x2)); // the last point (y2,x2) has to be the same with the last point of the algorithm }
我没有真比过哪个代码更高效,理论上应该是后者,因为后者与Bresenham算法一样只使用了Integer Arithmetic。
基本图元的像素化—三角形像素化
三角形的像素化其实有两种思路去实现,一种是基于像素点的位置,一种是基于直线像素化。
算法5—基于像素位置判断的三角形像素化
首先我们有比较经典的Point in Triangle算法,StackOverFlow上有各种对“How to determine a point is in a triangle”这样问题的回答,被引用的比较多的是下面这一段代码:
static float sign(Point2d p1, Point2d p2, Point2d p3) { return (float)((p1.X - p3.X) * (p2.Y - p3.Y) - (p2.X- p3.X) * (p1.Y - p3.Y)); } static bool PointInTriangle(Point2d pt, Point2d v1, Point2d v2, Point2d v3) { bool b1, b2, b3; b1 = sign(pt, v1, v2) < 0.0f; b2 = sign(pt, v2, v3) < 0.0f; b3 = sign(pt, v3, v1) < 0.0f; return ((b1 == b2) && (b2 == b3)); }
上面的代码使用了向量叉积和向量夹角的的一些几何知识,核心思想是判断点对三角形三条边的三个张角是不是至少有两个钝角。假如有了这个函数,那么一个简单粗暴的三角形像素化的方法是,对三角形ABC的BOX范围的所有像素点,进行一次PointInTriangle的判断,在三角形内则涂色。不过此法过于粗暴,因而效率不高,不建议使用。
算法6—基于直线像素化的三角形像素化
还有一种做法略显奇葩,不过在这里介绍一下,之后的三维体素化会用到这个方法,这个方法可以被称作“连线法”。其大致思路是:先用Bresenham法连接ABC中任意一边,假如是BC,连的时候顺便记录下涂上的所有像素。之后使用画SuperCover线算法来依次连接A与这些像素。
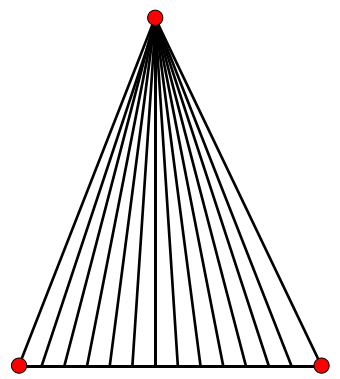
这个方法为什么不会漏填像素,可以简单的用反证法证明一下:例如下图中,假设漏填了像素P,则根据SuperCover线的定义,不可能有任何连线是经过P的,则连线至多相对P处于图中那两个射线的状态,由于像素方块的大小都是一样的,则必然出现比P更远位置的A像素,其也没有被任何线穿过。而上述算法中需要依次连接BC上所有的像素点与A,这样不可能出现A像素,因而矛盾,故这算法是逻辑正确的。

代码贴上来:
static void FillTriangle_Alg_2(ByteMatrix& bmp,Point2d p0,Point2d p1,Point2d p2) { std::vector<Point2d> plist; Bresenham(bmp,p1,p2,plist); for(int i=0;i<plist.size();i++) { SuperCover(bmp,plist[i],p0); } }
算法7—基于直线像素化的三角形像素化思路2
个人认为其实在二维平面空间上最具效率的三角形像素化方法是这个方法,叫做填充法。其思路是先使用Super算法涂上三角形ABC的三条边。然后利用三角形的重心一定在三角形内这个性质,找到三角形重心所对应的像素P,然后以P为种子点执行漫水填充算法。有相关基础的人应该都清楚这个漫水填充算法,在之前的博文里也有详细的说明这算法的几种实现方式。以P为种子点执行8向漫水填充,遇到已经被填充的则会停止,这样使得内部的像素被涂上颜色,即完成三角形像素化。其实现代码如下:
static void FillTriangle_Alg_3(ByteMatrix& bmp,Point2d p0,Point2d p1,Point2d p2) { Box2d box; box.UpdateRange(p0.X,p0.Y); box.UpdateRange(p1.X,p1.Y); box.UpdateRange(p2.X,p2.Y); Point2d seed((box.XMin+box.XMax)/2,(box.YMin+box.YMax)/2); SuperCover(bmp,p0,p1); SuperCover(bmp,p0,p2); SuperCover(bmp,p1,p2); FloodFill(bmp,seed); }
测试数据展示
在30*30的ByteMatrix上测试画线算法的输出:
 |
 |
 |
 |
| 算法1-DDA | 算法2-Bresenham | 算法3-CrossPixels | 算法4—Enhanced Bresenham |
在30*30的ByteMatrix上测试画三角形算法的输出:
 |
 |
 |
| 算法5输出三角形 | 算法6输出三角形 | 算法7输出三角形 |
多边形像素化
综合了上面讲的算法,则不难想出像素化一般平面几何图形的方法,无非是下面两个思路:
- 将多边形三角化,然后对所有三角形像素化。
- 将多边形的边像素化,然后在多边形内部选择种子点进行漫水填充算法。
任意多边形三角化的方法在关于轮廓线的博文中有提到这里就不重复贴了。第二种采取漫水填充法的思路中涉及到如何找到一个种子点的问题,因为任意多边形的重心不见得一定在图形内部,故漫水填充算法可以采用一种逆向思路,即先填充图形外部,再反色,即可以得到多边形的像素化。关于这部分,思路其实比较简单直接,就不贴代码了。算法1-7的相关完整工程代码下载链接:
https://github.com/chnhideyoshi/SeededGrow2d/tree/master/DrawLine2d
爬网的太疯狂了,转载本文要注明出处啊:http://www.cnblogs.com/chnhideyoshi/


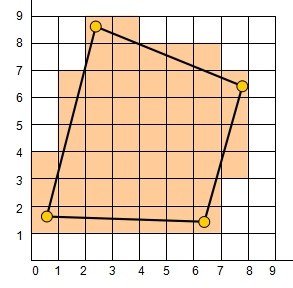 学计算机的人往往都比较清楚图形和图像的区别,而且往往能够从数据结构的角度理解这两者的区别,一般来说,图形是由几何空间中的基本图元所组成,表现为用外部轮廓线条勾勒成的矢量图。例如由计算机绘制的直线、圆、矩形、曲线、图表等。而图像是由扫描仪、摄像机等输入设备捕捉实际的画面产生的数字图像,是由像素点阵构成的位图。例如在二维几何空间中,同样是为了表述一个四边形,从图形的角度去看,需要提供四个顶点的坐标作为基本图元,然后提供一个画线的指令,将四个顶点按顺序提供出来。而从图像的角度看,一个四边形需要映射为一个特定分辨率位图上的像素集合。
学计算机的人往往都比较清楚图形和图像的区别,而且往往能够从数据结构的角度理解这两者的区别,一般来说,图形是由几何空间中的基本图元所组成,表现为用外部轮廓线条勾勒成的矢量图。例如由计算机绘制的直线、圆、矩形、曲线、图表等。而图像是由扫描仪、摄像机等输入设备捕捉实际的画面产生的数字图像,是由像素点阵构成的位图。例如在二维几何空间中,同样是为了表述一个四边形,从图形的角度去看,需要提供四个顶点的坐标作为基本图元,然后提供一个画线的指令,将四个顶点按顺序提供出来。而从图像的角度看,一个四边形需要映射为一个特定分辨率位图上的像素集合。

 浙公网安备 33010602011771号
浙公网安备 33010602011771号