之前的文章讨论了三角网格，顶点焊接这个主题是由三角网格建模衍生出来的。简单点说，顶点焊接又可以叫做“顶点去重”，就是要在Mesh中去除重复的顶点。由之前的介绍Mesh的文章可以知道，Mesh实际上就是顶点的集合+三角形的集合，其中三角形是由三个指向顶点集合的索引表示的。
什么是顶点焊接？
之前的文章讨论了三角网格，顶点焊接这个主题是由三角网格建模衍生出来的。简单点说，顶点焊接(Vertex Welding)又可以叫做“顶点去重”，就是要在Mesh中去除重复的顶点，或者说去掉位置相重合的顶点，使之成为一个顶点，这样共有这些顶点的三角形就被“焊接”了起来。由之前的介绍Mesh的文章可以知道，Mesh实际上就是顶点的集合+三角形的集合，其中三角形是由三个指向顶点集合的索引表示的。但在实际应用中，Mesh往往是从一种原始的三角形集合（triangle soup）中建立的，这种原始三角形集合中的三角形全部都是独立的三角片，每个三角片直接包含了三个顶点的坐标而不是顶点索引。也就是说，这些三角形的顶点在数据结构上彼此是相互独立的，例如三角形A和三角形B中均含有坐标为P（1，0，1）的顶点，在几何意义上应该是相同的点，但在原始三角形集合中，完全看不出这种三角形共用顶点这样的关系。从这样的原始三角形中建立一个能正确表达顶点之间的连接方式的Mesh，就需要从这种“原始三角形集合”中提取不重复的顶点集合，再将这些三角形转化为基于顶点索引的三角形。这样才是成功的创建了一个去除冗余信息，能够表达正确连接关系的Mesh。在建立了这样的Mesh后，前面所提到的三角形A和B才是真正意义上共有了顶点P，因为他们会同时具有相等的P的顶点索引。
下图说明原始三角形集合和去重之后创建的正确的Mesh。简单点说，在顶点焊接之前，三角形之间是完全独立的。在顶点焊接之后，在几何上等价的三角形顶点就被融合在一起，变成一个顶点，实现了三角形顶点的共用。
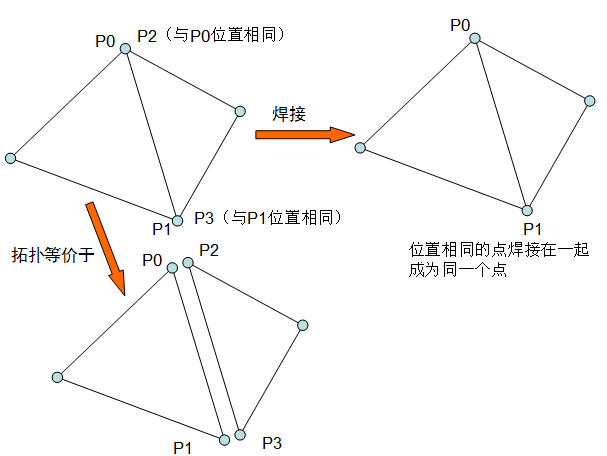
为什么要焊接顶点
假如不进行顶点焊接，从原始三角形集合中，仍然可以象征性产生一个Mesh。假如一个具有N个三角形的原始三角形集合，我们不考虑重复的顶点，直接为它建立一个Mesh数据结构，那么这个Mesh就是一个具有3*N个顶点和N个三角形的Mesh。这样的Mesh和经过了顶点焊接之后的Mesh有如下几个相同点和不同点：
相同点：
都可以用于Flat渲染。由于Flat渲染就是渲染每一个组成模型的三角面片，所以无论这些三角片的顶点是否有共用的，不影响最后渲染效果。简单的说，这样的应用方式只需要三角片集合，有了三角片集合，就能渲染出模型的形状。
不同点：
- 首先去重之后的Mesh占内存空间要小于未去重的Mesh，这一点显而易见。所以对于一个需要节省空间的应用，或者需要对Mesh进行输出保存，都需要使用去重之后的Mesh，这样省去了记录重复顶点的空间。
- 由于未去重的Mesh的三角形实际上都是相互独立的，所以无法正确计算邻接面，邻接点这些信息（非要计算会发现每个顶点就只有一个邻接面，这样已无意义），所以无法对其进行网格平滑，削减等Mesh处理，同时也无法进行基于点法向的渲染，因为计算点法向需要正确的邻接面信息。
- 焊接前的Mesh只是独立的三角片集合，焊接之后才真正意义上有了拓扑结构，这样无论顶点的坐标如何改变，Mesh的拓扑不会变，模型也不会出现缝隙。而未焊接的Mesh虽然可能每个三角形在位置上能连接成一个无缝的表面，但任何一个顶点坐标发生改变，就会使模型表面产生空隙。
所以说，顶点焊接（去重）是在很多应用环境下所必须研究的问题。
顶点焊接的方法
一、排序去重
对于一个n个整数组成的一维数组，一个常用的去重算法是先排序再遍历，时间复杂度为O(n*logn)。排序之后，相等的数会成连续排列，利用一次循环O(n)时间，将每次新发现的数覆盖到旧数的位置，即可去重，总时间复杂度还是O(n*logn)。代码如下：
public class QuickSorter<T> where T : IComparable<T> { public T[] A { get; set; } public void Sort() { QuickSort(A, 0, A.Length - 1); } public void QuickSort(T[] A, int st, int ed) { if (st < ed) { int pa = Partition(A, st, ed, (st + ed) / 2); QuickSort(A, st, pa - 1); QuickSort(A, pa + 1, ed); } } public static void Swap<T>(T[] A, int index1, int index2) { T temp = A[index1]; A[index1] = A[index2]; A[index2] = temp; } private int Partition(T[] A, int st, int ed, int partionPos)//SELECT VALUE ON PAPOS AND MAKE THE ARRAY(ST TO ED) INTO TWO PARTS: BEFORE RET SMALLER THAN VALUE AFTER BIGGER { if (partionPos != st) Swap(A, partionPos, st); T value = A[st]; int boundary = st;//BOUNDARY REFER TO THE LAST SMALLER INDEX for (int i = st + 1; i <= ed; i++) { if (A[i].CompareTo(value) < 0) { if (boundary + 1 != i) Swap(A, i, boundary + 1); boundary++; } } if (st != boundary) Swap(A, boundary, st); return boundary; } }//quick sort class
以上是排序的代码，下面的去重的代码：
public static int RemoveDuplicates<T>(T[] data) where T:IComparable<T> { QuickSorter<T> sorter = new QuickSorter<T>(); sorter.A = data; sorter.Sort();//first needs sorting int lastIndex = 0; for (int i = 0; i < data.Length; i++) { if (data[i].CompareTo(data[lastIndex])==0) { continue; } else { data[lastIndex + 1] = data[i]; lastIndex++; } } return lastIndex + 1; }//remove duplicates in an T array
在本文顶点焊接这个应用场合，假定已经获得了原始三角形集合List<OriginalTriangle>，则需要排序的不是整数而是由三个浮点数及其索引组成的Point3dWidthIndex结构，可以预先对这个结构指定一种偏序关系，比如比较两个点大小可以依次使用X、Y、Z坐标的大小来决定。这样就可以对长为3*N的点集数组进行排序去重。不过还需要考虑的是：由于三角形集合中的三角形需要关联着这个点集的索引，所以必须记录下三角形顶点旧索引所对应的新索引的位置。通过使用辅助信息的数组可以办到。使用类似的思想，可实现如下的基于排序的顶点焊接。
public struct OriginalTriangle { public Point3d P0; public Point3d P1; public Point3d P2; public OriginalTriangle(int x0,int y0,int z0,int x1,int y1,int z1,int x2,int y2,int z2) { P0.X=x0; P0.Y=y0; P0.Z=z0; P1.X=x1; P1.Y=y1; P1.Z=z1; P2.X=x2; P2.Y=y2; P2.Z=z2; } } public struct Point3dWithIndex :IComparable<Point3dWithIndex> { public Point3d P; public int Index; public Point3dWithIndex(Point3d p, int index) { P = p; Index = index; } public int CompareTo(Point3dWithIndex other) { if (P.X != other.P.X) return P.X.CompareTo(other.P.X); else { if (P.Y != other.P.Y) return P.Y.CompareTo(other.P.Y); else { if (P.Z != other.P.Z) return P.Z.CompareTo(other.P.Z); else return 0; } } } }
public static Mesh WeldingVertices(List<OriginalTriangle> triangleSoup) { Mesh mesh=new Mesh(); Point3dWithIndex[] pointArray = new Point3dWithIndex[triangleSoup.Count * 3]; int lindex=0; for (int i = 0; i < triangleSoup.Count; i++) { pointArray[lindex].P = triangleSoup[i].P0; pointArray[lindex+1].P = triangleSoup[i].P1; pointArray[lindex+2].P = triangleSoup[i].P2; pointArray[lindex].Index = lindex; pointArray[lindex + 1].Index = lindex + 1; pointArray[lindex + 2].Index = lindex + 2; Triangle t=new Triangle(); t.P0Index=lindex; t.P1Index=lindex+1; t.P2Index=lindex+2; mesh.AddFace(t); lindex += 3; } QuickSorter<Point3dWithIndex> sorter = new QuickSorter<Point3dWithIndex>(); sorter.A = pointArray; sorter.Sort(); int[] tempArray = new int[pointArray.Length]; for (int i = 0; i < pointArray.Length; i++) { tempArray[pointArray[i].Index] = i; } int lastIndex = 0; for (int i = 0; i < pointArray.Length; i++) { if (pointArray[i].CompareTo(pointArray[lastIndex]) == 0) { continue; } else { pointArray[lastIndex + 1] = pointArray[i]; tempArray[pointArray[i].Index] = lastIndex + 1 ; lastIndex++; } } for (int i = 0; i < lastIndex; i++) { mesh.AddVertex(pointArray[i].P); } for (int i = 0; i < mesh.Faces.Count; i++) { Triangle t = mesh.Faces[i]; t.P0Index = tempArray[mesh.Faces[i].P0Index]; t.P1Index = tempArray[mesh.Faces[i].P1Index]; t.P2Index = tempArray[mesh.Faces[i].P2Index]; mesh.Faces[i] = t; } return mesh; }
二、哈希表去重
基于排序的顶点焊接有如下的不足：
- 需要一定辅助空间。
- 排序必须针对已经建立好的集合，如上文的List<OriginalTriangle>，但很多时候原始三角形并不需要被存储为一个集合，而是依次产生后被销毁。这样就需要“来一个焊接一个”这样来焊接成Mesh。
去重并非只有排序去重这一种思路，比如针对整数数组去重，还有一种基于哈希表的方法。这种方式不需要进行排序，但需要使用哈希表来标定一个元素是否已被加入。该算法需遍历一次数组，依次访问每个数并检查其是否在哈希表中，若不在则加入哈希表，若在则继续下一个数。利用哈希表能快速访问键值的特点，这种方法也是一种好的实现，但其时间和空间效率很大程度决定于哈希表的设计。
回到顶尖焊接这个引用场合，由于顶点是三个浮点数坐标组成的结构，所以这个结构应当作为哈希表的键，而哈希表的值可以定为int，表示新的不重复点集的索引i，指示当前的点已经被放在点集的第i个位置，那么对于任何一个点，访问他对应的哈希表位置，若已存在i值，表示这个点前面已经被加入过不重复点集，这次已至少是是第二此访问了；而若没有i值，表面这个点是个新点，该被加入不重复点集。
那么关键就在于这个哈希映射函数怎么设计。对于没有任何约束的float三元组设计一种哈希映射函数，将点结构映射为哈希值索引。这里我们不详细讨论这种无范围限定的点结构是如何计算到哈希值。直接采用.NET自带哈希表进行焊接实现，代码如下：
interface IHashTable<T> { void SetHashValue(int x, int y, int z,T value); bool GetHashValue(int x, int y, int z,ref T value); void SetDefaultValue(T value); void Clear(); }
class HashTable_General<T>:IHashTable<T> { Dictionary<Point3d, T> hashTable = new Dictionary<Point3d, T>(); public void SetHashValue(int x, int y, int z, T value) { Point3d p = new Point3d(x, y, z); hashTable.Add(p, value); } public bool GetHashValue(int x, int y, int z, ref T value) { Point3d p = new Point3d(x, y, z); if (hashTable.ContainsKey(p)) { value = hashTable[p]; return true; } else { return false; } } public void SetDefaultValue(T value) { return; } public void Clear() { return; } }
.NET自带的Dictionary<TKey,TValue>类型会用一种通行的方式去为TKey类型的键计算哈希值。本文就不详述.NET内部如何实现这个哈希表，而重点将放在有条件约束的点坐标三元组的哈希映射设计上。
针对三维数据场整数坐标的哈希表去重特殊处理方法
在很多应用场合，参与去重的顶点集合往往具备如下的特点：X、Y、Z坐标均在一个范围之内，如（0~width-1,0~height-1,0~depth-1）；X、Y、Z坐标均为非负整数。对于这样一种特殊场合，顶点去重有如下几种实现方法。
- 基于三维数组的哈希表
- 基于二维数组的哈希表
- 基于双二维数组的哈希表
基于三维数组的哈希表
使用bool三维数组，三维数组的每个单元对应一个整点是否被访问过。使用这种方式实现的哈希表代码如下：
class HashTable_3dArray<T>:IHashTable<T> { T[,,] array3d; int width; int height; int depth; T defaultValue; public HashTable_3dArray(int width, int height, int depth) { this.width = width; this.height = height; this.depth = depth; array3d = new T[width,height,depth]; } public void SetHashValue(int x, int y, int z,T value) { array3d[x ,y , z] = value; } public bool GetHashValue(int x, int y, int z,ref T value) { value = array3d[x ,y , z]; return true; } public void Clear() { return; } public void SetDefaultValue(T value) { defaultValue = value; for (int i = 0; i < width; i++) { for (int j = 0; j < height; j++) { for (int k = 0; k < depth; k++) { array3d[i, j, k] = value; } } } } }
利用三维数组实现的哈希表，特点是访问迅速，但缺点很明显：空间效率太差。假设一个Mesh的顶点所在的坐标范围为X1~X2,Y1~Y2,Z1~Z2。这种哈希表至少需要(X2-X1+1)*(Y2-Y1+1)*(Z2-Z1+1)的空间来对应所有可能的点，本文的例子是占用了width*height*depth的空间。实际应用中这样的空间效率往往是不可接受的。实际情况往往Mesh的顶点只能占到点集范围总空间其中的很小一部分，大部分的位置是没有点的，也是访问不到的。
基于二维数组的哈希表
使用二元组集合为单位的二维数组来实现哈希表，牺牲了时间效率，换取完全可以接受的空间效率，因为减少了一维意味着减少了数量级的空间。此时点集范围空间上的所有点仅以(X,Y)坐标映射到二维数组上，而不像三维数组哪像采用(X,Y,Z)三个坐标。遇到(X,Y)坐标相同的点，将其在二维数组的(X,Y)处以一维数组的方式“堆砌”起来。在查找时对(X,Y)处数组顺序查找，插入时末端插入即可。这种方式实现的哈希表代码如下：
public class HashTable_2dArray<T>:IHashTable<T> { struct DepthAndValue<T1> { public int K; public T1 Value; public DepthAndValue(int k, T1 value) { K = k; Value = value; } }//二元组，用来保存第三维索引和映射值 List<DepthAndValue<T>>[,] mapHash; int width; int height; int depth; public HashTable_2dArray(int width,int height,int depth) { this.width = width; this.height = height; this.depth = depth; mapHash = new List<DepthAndValue<T>>[this.width, this.height]; } public void SetHashValue(int x, int y, int z, T value) { if (mapHash[x, y] == null) { mapHash[x, y ] = new List<DepthAndValue<T>>(); mapHash[x, y].Add(new DepthAndValue<T>(z, value)); } else { mapHash[x,y].Add(new DepthAndValue<T>(z, value)); } } static int FindK(List<DepthAndValue<T>> list, int k) { for (int i = 0; i < list.Count; i++) { if (list[i].K == k) return i; } return -1; } public bool GetHashValue(int x, int y, int z, ref T value) { if (mapHash[x, y] != null) { int index = FindK(mapHash[x, y], z); if (index == -1) { return false; } else { value = mapHash[x, y][index].Value; return true; } } else return false; } public void SetDefaultValue(T value) { return; } public void Clear() { return; } }
这种方式将某两维相同但第三维不同的点堆砌起来，显然访问效率不如三维数组的实现，是一种时间换空间的手段。考虑到多数Mesh的形状在X,Y平面映射上分布均匀，这种方式是实现哈希表的一种很好的思路，不过这种方式也不是没有问题。
这种方式实现的哈希表需要考虑如下两个问题：
- 究竟采用哪两维做二维数组比较好？本文例子采用了XY维,Z索引堆砌，实际上XZ维,Y索引堆砌或者YZ维,X堆砌也是可以的。这个问题涉及Mesh的形态，一般来说，一个Mesh在某两维上的投影较为均匀，则这两维适合作为哈希表二维数组的选择。
- 在不能预先知道Mesh形状的情况下，不可避免会出现某些位置堆砌过高的问题。例如太多的点都具有相同的两维坐标，如正方体这样的形状。无论采用哪两维。都会出现二维数组某些位置上堆砌过高的问题。这样会使得顺序查找的时间大大增加。
基于双二维数组的哈希表
为了解决上述基于二维数组哈希表在特殊场合时间效率不高的问题，这里引入双二维数组哈希表。这种哈希表采用两个二维数组来存放原来只由一个二维数组存放的二元组集合。在任何一个点（X,Y,Z）插入哈希表时，插入的位置就有两个选择：比如堆砌到(X,Y)处集合的最后一个位置，或者是(Y,Z)处集合的最后一个位置。选择依据是哪个集合更小。在查找时则需要同时搜寻(X,Y)处集合和(Y,Z)处集合。由于这种方式使得集合平均大小大为减小，所以针对正方体这样的具有大量两个维度坐标都相等的点的特殊形状，有很好的效率。因为任何一个表示实物模型的Mesh顶点集合，是不可能同时在XY，YZ，XZ中的任何两维同时产生堆砌过高的问题。
相应的代码如下：
public class HashTable_Double2dArray<T>:IHashTable<T> { struct IndexAndValue<T1> { public int Index; public T1 Value; public IndexAndValue(int index, T1 value) { Index = index; Value = value; } } List<IndexAndValue<T>>[,] mapHashXY; List<IndexAndValue<T>>[,] mapHashXZ; int width; int height; int depth;public HashTable_Double2dArray(int width, int height, int depth) { this.width = width ; this.height = height ; this.depth = depth ; mapHashXY = new List<IndexAndValue<T>>[this.width, this.height]; mapHashXZ = new List<IndexAndValue<T>>[this.width, this.depth]; } static int FindK(List<IndexAndValue<T>> list, int index) { for (int i = 0; i < list.Count; i++) { if (list[i].Index == index) return i; } return -1; } public void SetHashValue(int x, int y, int z, T value) { if (mapHashXY[x, y] == null) { mapHashXY[x, y] = new List<IndexAndValue<T>>(); mapHashXY[x, y].Add(new IndexAndValue<T>(z, value)); } else { if (mapHashXZ[x, z] == null) { mapHashXZ[x, z] = new List<IndexAndValue<T>>(); mapHashXZ[x, z].Add(new IndexAndValue<T>(y, value)); } else { if (mapHashXY[x, y].Count > mapHashXZ[x, z].Count) { mapHashXZ[x, z].Add(new IndexAndValue<T>(y, value)); } else { mapHashXY[x, y].Add(new IndexAndValue<T>(z, value)); } } } } public bool GetHashValue(int x, int y, int z, ref T value) { if (mapHashXY[x, y] != null) { int index = FindK(mapHashXY[x, y], z); if (index == -1) { if (mapHashXZ[x, z] != null) { int index2 = FindK(mapHashXZ[x, z], y); if (index2 == -1) return false; else { value = mapHashXZ[x, z][index2].Value; return true; } } else { return false; } } else { value = mapHashXY[x, y][index].Value; return true; } } else return false; } public void SetDefaultValue(T value) { return; } public void Clear() { return; } }
哈希表去重的实现
在已获得原始三角形集合之后，使用其进行焊接之后生成Mesh的代码如下：
public static Mesh WeldingVertices_Hash(List<OriginalTriangle> triangleSoup) { Mesh mesh = new Mesh(); IHashTable<int> hash = new HashTable_General<int>(); //IHashTable<int> hash = new HashTable_3dArray<int>(); //IHashTable<int> hash = new HashTable_2dArray<int>(); //IHashTable<int> hash = new HashTable_Double2dArray<int>(); for (int i = 0; i < triangleSoup.Count; i++) { Triangle t = new Triangle(); Point3d p0 = triangleSoup[i].P0; Point3d p1 = triangleSoup[i].P1; Point3d p2 = triangleSoup[i].P2; int temp = -1; int index0, index1, index2; if (hash.GetHashValue((int)p0.X, (int)p0.Y, (int)p0.Z, ref temp)) { index0 = temp; } else { index0 = mesh.AddVertex(p0); } if (hash.GetHashValue((int)p1.X, (int)p1.Y, (int)p1.Z, ref temp)) { index1 = temp; } else { index1 = mesh.AddVertex(p1); } if (hash.GetHashValue((int)p2.X, (int)p2.Y, (int)p2.Z, ref temp)) { index2 = temp; } else { index2 = mesh.AddVertex(p2); } t.P0Index = index0; t.P1Index = index1; t.P2Index = index2; mesh.AddFace(t); } return mesh; }
在更多的情况下，原始三角形不需要用集合保存起来，往往是每生成一个三角形，就将其焊接到已有的Mesh上，为此特别定义一个MeshBuilder类，用于将依次生成的三角形进行焊接，只需要调用AddTriangle方法即可。这个类会在之后探讨SMC算法的时候涉及到。
class MeshBuilder { Mesh mesh; IHashTable<int> hashMap; int width; int height; int depth; public MeshBuilder(int width, int height, int depth,IHashTable<int> hashtable) { this.width = width; this.height = height; this.depth = depth; mesh = new Mesh(); this.hashMap = hashtable; } public void AddTriangle(int p0x, int p0y, int p0z, int p1x, int p1y, int p1z, int p2x, int p2y, int p2z) { int p0i; int p1i; int p2i; int index = 0; bool hasValue; hasValue = hashMap.GetHashValue(p0x, p0y, p0z, ref index); if (!hasValue) { p0i = mesh.AddVertex(new Point3d(p0x, p0y, p0z)); hashMap.SetHashValue(p0x, p0y, p0z, p0i); } else { p0i = index; } hasValue = hashMap.GetHashValue(p1x, p1y, p1z, ref index); if (!hasValue) { p1i = mesh.AddVertex(new Point3d(p1x, p1y, p1z)); hashMap.SetHashValue(p1x, p1y, p1z, p1i); } else { p1i = index; } hasValue = hashMap.GetHashValue(p2x, p2y, p2z, ref index); if (!hasValue) { p2i = mesh.AddVertex(new Point3d(p2x, p2y, p2z)); hashMap.SetHashValue(p2x, p2y, p2z, p2i); } else { p2i = index; } Triangle t = new Triangle(p0i, p1i, p2i); mesh.AddFace(t); } public Mesh GetMesh() { return mesh; } public void Clear() { hashMap.Clear(); } }
性能测评
实验采用来自volvis.org的Engine数据和Lobster数据，以及创造的Cube数据所生成的表面网格文件（PLY格式）。三个文件的预览图如下：
| 数据预览 |  |
 |
 |
| 数据名称 | Lobster.ply | engine.ply | cube.ply |
| 数据描述 | 具有高不规则度 | 不规则度适中 | 规则度高，有大量的顶点的X,Y坐标均相同 |
时间结果如下，其中构建时间1、2、3、4分别对应.NET内置哈希表、3维数组哈希表、2维数组哈希表和双2维数据哈希表：
| 数据 | 顶点数 | 面数 | 构建时间1 | 构建时间2 | 构建时间3 | 构建时间4 | 结果顶点数 | 焊接后减少顶点比例 |
| lobster.ply | 544104 | 181368 | 21ms | 19ms | 21ms | 22ms | 87974 | 83.8% |
| engine.ply | 1301202 | 433734 | 47ms | 35ms | 42ms | 44ms | 216829 | 83.3% |
| cube.ply | 1439988 | 479996 | 58ms | 38ms | 59ms | 42ms | 240000 | 83.3% |
从上述结果可以看出，顶点焊接有效减少了重复顶点，同时不同的哈希表针对有不同形态特点的数据也有不同的性能。
结论
使用哈希表是顶点焊接的有效办法，哈希表的设计决定了焊接的时间和空间效率。在本文整数顶点坐标焊接的应用中，基于三维数组的哈希表时间效率最高，但空间效率最差；基于二维数组的哈希表在顶点分布不规则的场合具有较好的时间和空间效率；基于双二维数组的哈希表在顶点分布较为规则的顶点焊接中具有较好时间效率。而在不规则的场合则一般要慢于基于单二维数组的哈希表。
爬网的太疯狂了，转载本文要注明出处啊：http://www.cnblogs.com/chnhideyoshi/
