chnhideyoshi

Focus On Algorithm Implementation On Geometry Processing & Scientific Visulization & Image Processing
  :: :: 博问 :: 闪存 :: :: :: :: 管理 ::
一种适合于MC与SMC算法的哈希表设计

MC算法与SMC算法中的三角片焊接问题

　　在之前的关于MC算法与SMC算法的博文中介绍了算法的实现，文章主要围绕算法的核心问题，即三角片如何产生的问题进行了详细的描述。但由于实际应用中需要的等值面Mesh数据不是三角片的简单并集，所以需要进行所谓的顶点焊接(Vertex Welding)来生成正确的拓扑结构以反应三角片之间的共用顶点关系。顶点焊接，简单的说就是把三角片中重合的顶点算作一个顶点加入顶点集。在之前博文中的代码实现里，采用了一种MeshBuilder类来实现这样的顶点焊接。其核心思想是采用哈希表来避免顶点的重复加入，逻辑简单点说就是下面这几步：

  1. 对三角片集合中的所有三角形
    1.  对三角形的三个顶点
      1. 若顶点P在哈希表中不存在
        1. 将顶点P加入顶点列表
        2. 将P加入哈希表
  2. 结束循环

　　采用的哈希表是根据点坐标来计算哈希值的，这样相同的点必然对应一样的哈希值。这样重复的点就不会再被加入顶点列表。由于哈希表理论上有很好的存取速度，故MC算法和SMC算法即可采用此逻辑来将体元中的三角片焊接成具有拓扑结构的Mesh。

　　

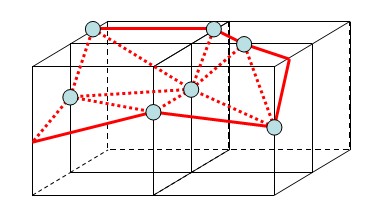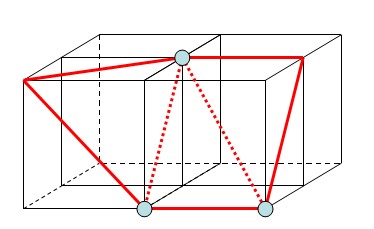MC算法的焊接顶点 SMC算法的焊接顶点

 

 

一种新的设计

　　上文所述的实现方式是为了突出MC、SMC算法的“从每个体元中抽取三角片”的主逻辑而简化了顶点焊接的逻辑。事实上，采用上文说的哈希表会存在一定的时间和空间效率问题。之前的另一篇关于顶点焊接的文章“浅议顶点焊接与哈希表的设计”提出的几种哈希表，不能很好的同时兼顾时间和空间效率。在数据规模较大的情况下，顶点焊接逻辑很容易就成为算法的瓶颈。

　　例如使用三维数组哈希表，很明显需要sizeof(long)*with*height*depth的空间，是巨大的空间消耗。而使用二维数组堆砌哈希表，则容易让更多的时间花费在顺序查找链表上。归根结底，这些将顶点所有可能位置都考虑到的哈希表，没有充分利用MC/SMC算法三角片产生的局部特点。

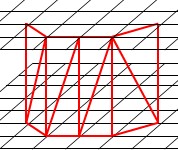
　　考虑到MC/SMC中三角片是逐个从体元中抽取的，这样只有相邻两层的三角片顶点才可能产生重复现象如下图，那么三角片的产生，应该可以这样考虑：

  1. 抽取第i层体元的三角片并焊接之
  2. 抽取第i+1层体元的三角片并焊接之
  3. 焊接第i层三角片与第i+1层三角片

　　为此，可以设计一个有两层二维数组组成的哈希表，二维数组的尺寸都是width*height。用以表示一层体元上下两层顶点的可能的哈希位置。每抽取完一层的体元，这两层数组会往下自动推进一层，同时还需要有变量记录当前指示的层位置。

　　对于SMC算法，由于顶点只能在格点上，故基于此原理的哈希表可以实现如下：

class SMCTriangleNetHashTable
{
    public int CurrentLayerIndex;

    int stx;
    int sty;
    int width;
    int height;
    List<int[,]> mapList;
    public SMCTriangleNetHashTable(int minx, int miny, int width, int height)
    {
        this.stx = minx - 1;
        this.sty = miny - 1;
        this.width = width + 2;
        this.height = height + 2;
        mapList = new List<int[,]>(2);
        mapList.Add(new int[this.width, this.height]);
        mapList.Add(new int[this.width, this.height]);
        SetDefaultValue(0);
        SetDefaultValue(1);
    }
    public void SetDefaultValue(int index0_1)
    {
        for (int i = 0; i < width; i++)
        {
            for (int j = 0; j < height; j++)
            {
                mapList[index0_1][i, j] = -1;
            }
        }
    }
    public void IncreaseIndex()
    {
        CurrentLayerIndex++;
        SetDefaultValue(0);
        int[,] temp = mapList[0];
        mapList[0] = mapList[1];
        mapList[1] = temp;
    }
    public void SetHashValue(int x, int y, int z, int value)
    {
        int index0_1 = z - CurrentLayerIndex;
        mapList[index0_1][x - stx, y - sty] = value;
    }
    public int GetHashValue(int x, int y, int z)
    {
        int index0_1 = z - CurrentLayerIndex;
        return mapList[index0_1][x - stx, y - sty];
    }
}

　　这样SMC算法的实现形式如下：

public class SMCProcessor
{
    struct OriginalTriangle
    {
        public Int16Triple P0;
        public Int16Triple P1;
        public Int16Triple P2;
        public OriginalTriangle(int p0x, int p0y, int p0z, int p1x, int p1y, int p1z, int p2x, int p2y, int p2z)
        {
            P0.X = p0x;
            P0.Y = p0y;
            P0.Z = p0z;
            P1.X = p1x;
            P1.Y = p1y;
            P1.Z = p1z;
            P2.X = p2x;
            P2.Y = p2y;
            P2.Z = p2z;
        }
    }
    public static byte VULF = 1 << 0;
    public static byte VULB = 1 << 1;
    public static byte VLLB = 1 << 2;
    public static byte VLLF = 1 << 3;
    public static byte VURF = 1 << 4;
    public static byte VURB = 1 << 5;
    public static byte VLRB = 1 << 6;
    public static byte VLRF = 1 << 7;
    //以上为体素为实点的位标记
    public static Int16Triple[] PointIndexToPointDelta = new Int16Triple[8]
    {
        new Int16Triple(0, 1, 1 ),
        new Int16Triple(0, 1, 0 ),
        new Int16Triple(0, 0, 0 ),
        new Int16Triple(0, 0, 1 ),
        new Int16Triple(1, 1, 1 ),
        new Int16Triple(1, 1, 0 ),
        new Int16Triple(1, 0, 0 ),
        new Int16Triple(1, 0, 1 )
    };//体元内每个体素相对基准体素坐标的偏移
    public static byte[] PointIndexToFlag = new byte[8]
    {
        VULF,
        VULB,
        VLLB,
        VLLF,
        VURF,
        VURB,
        VLRB,
        VLRF
    };//每个体素对应的位标记
    BitMap3d bmp;
    int d;
    int h;
    int w;
    int wh;
    public SMCProcessor(BitMap3d bitmap)
    {
        this.bmp = bitmap;
    }
    public Mesh GenerateSurface()
    {
        d = bmp.depth;
        h = bmp.height;
        w = bmp.width;
        wh = w * h;
        Int16Triple[] temp = new Int16Triple[8];
        Mesh m = new Mesh();
        OriginalTriangle[] tempTriangles = new OriginalTriangle[4];
        SMCTriangleNetHashTable hash = new SMCTriangleNetHashTable(0, 0, w, h);

        for (int k = 0; k <= d - 1; k++)
        {
            for (int j = 0; j <= h - 1; j++)
            {
                for (int i = 0; i <= w - 1; i++)
                {
                    byte value = GetConfig(temp, bmp, i, j, k);
                    if (value == 0 || value == 255)
                        continue;
                    int tcount = ExtractTriangles(temp, value, i, j, k, tempTriangles);
                    for (int tindex = 0; tindex < tcount; tindex++)
                    {
                        MergeTriangleIntoMesh(m, hash, tempTriangles[tindex]);
                    }
                }
            }
            hash.IncreaseIndex();
        }
        return m;
    }

    private byte GetConfig(Int16Triple[] temp, BitMap3d flagsMap, int indexInWidth, int indexInHeight, int indexInDepth)
    {
        byte value = 0;
        for (int pi = 0; pi < 8; pi++)
        {
            temp[pi].X = indexInWidth + PointIndexToPointDelta[pi].X;
            temp[pi].Y = indexInHeight +PointIndexToPointDelta[pi].Y;
            temp[pi].Z = indexInDepth + PointIndexToPointDelta[pi].Z;
            if (temp[pi].X < w && temp[pi].X >= 0
                && temp[pi].Y < h && temp[pi].Y >= 0
                && temp[pi].Z < d && temp[pi].Z >= 0
                && bmp.data[temp[pi].X + w * (temp[pi].Y) + wh * (temp[pi].Z)] == BitMap3d.WHITE)
            {
                value |= PointIndexToFlag[pi];
            }
        }
        return value;
    }

    private int ExtractTriangles(Int16Triple[] temp, byte value, int indexInWidth, int indexInHeight, int indexInDepth, OriginalTriangle[] result)
    {
        int tcount = 0;
        if (SMCTable.TableFat[value, 0] != -1)
        {
            int index = 0;
            while (SMCTable.TableFat[value, index] != -1)
            {
                Int16Triple t0 = temp[SMCTable.TableFat[value, index]];
                Int16Triple t1 = temp[SMCTable.TableFat[value, index + 1]];
                Int16Triple t2 = temp[SMCTable.TableFat[value, index + 2]];
                result[tcount] = new OriginalTriangle(t0.X, t0.Y, t0.Z, t1.X, t1.Y, t1.Z, t2.X, t2.Y, t2.Z);
                tcount++;
                index += 3;
            }
        }
        return tcount;
    }

    private void MergeTriangleIntoMesh(Mesh mesh, SMCTriangleNetHashTable hashMap, OriginalTriangle ot)
    {
        int p0x = ot.P0.X;
        int p0y = ot.P0.Y;
        int p0z = ot.P0.Z;
        int p1x = ot.P1.X;
        int p1y = ot.P1.Y;
        int p1z = ot.P1.Z;
        int p2x = ot.P2.X;
        int p2y = ot.P2.Y;
        int p2z = ot.P2.Z;
        int p0i;
        int p1i;
        int p2i;
        int index = 0;
        index = hashMap.GetHashValue(p0x, p0y, p0z);
        if (index == -1)
        {
            p0i = mesh.AddVertex(new Point3d(p0x, p0y, p0z));
            hashMap.SetHashValue(p0x, p0y, p0z, p0i);
        }
        else
        {
            p0i = index;
        }

        index = hashMap.GetHashValue(p1x, p1y, p1z);
        if (index == -1)
        {
            p1i = mesh.AddVertex(new Point3d(p1x, p1y, p1z));
            hashMap.SetHashValue(p1x, p1y, p1z, p1i);
        }
        else
        {
            p1i = index;
        }

        index = hashMap.GetHashValue(p2x, p2y, p2z);
        if (index == -1)
        {
            p2i = mesh.AddVertex(new Point3d(p2x, p2y, p2z));
            hashMap.SetHashValue(p2x, p2y, p2z, p2i);
        }
        else
        {
            p2i = index;
        }

        Triangle t = new Triangle(p0i, p1i, p2i);
        mesh.AddFace(t);
    }
}

　　对于MC算法，由于定点不在格点上，而是在格子的边上，这样必须要把格子的边与格点坐标相对应。不难发现，从每一个格点出发，想着X,Y,Z轴正方向可以引三条边，这样每一个边都能按此方法找到所出发的格点。于是这样就可以构造一个二维数组：

class MCTriangleNetHashTable
{
    public int CurrentLayerIndex;

    int stx;
    int sty;
    int width;
    int height;
    List<int[,,]> mapList;
    public MCTriangleNetHashTable(int minx, int miny, int width, int height)
    {
        this.stx = minx - 1;
        this.sty = miny - 1;
        this.width = width + 2;
        this.height = height + 2;
        mapList = new List<int[,,]>(2);
        mapList.Add(new int[this.width, this.height,3]);
        mapList.Add(new int[this.width, this.height,3]);
        SetDefaultValue(0);
        SetDefaultValue(1);
    }
    public void SetDefaultValue(int index0_1)
    {
        for (int i = 0; i < width; i++)
        {
            for (int j = 0; j < height; j++)
            {
                mapList[index0_1][i, j, 0] = -1;
                mapList[index0_1][i, j, 1] = -1;
                mapList[index0_1][i, j, 2] = -1;
            }
        }
    }
    public void IncreaseIndex()
    {
        CurrentLayerIndex++;
        SetDefaultValue(0);
        int[,,] temp = mapList[0];
        mapList[0] = mapList[1];
        mapList[1] = temp;
    }
    public void SetHashValue(int x, int y, int z,int d, int value)
    {
        int index0_1 = z - CurrentLayerIndex;
        mapList[index0_1][x - stx, y - sty,d] = value;
    }
    public int GetHashValue(int x, int y, int z,int d)
    {
        int index0_1 = z - CurrentLayerIndex;
        return mapList[index0_1][x - stx, y - sty,d];
    }
}

　　基于此种设计的MC算法的实现代码如下：

public class MCProcessor
{
    struct OriginalTriangle
    {
        public Int16Triple CellCoord;
        public int E0;
        public int E1;
        public int E2;
        public OriginalTriangle(int x, int y, int z, int ei0, int ei1, int ei2)
        {
            CellCoord.X = x;
            CellCoord.Y = y;
            CellCoord.Z = z;
            E0 = ei0;
            E1 = ei1;
            E2 = ei2;
        }
    }
    public static byte VULF = 1 << 0;
    public static byte VULB = 1 << 1;
    public static byte VLLB = 1 << 2;
    public static byte VLLF = 1 << 3;
    public static byte VURF = 1 << 4;
    public static byte VURB = 1 << 5;
    public static byte VLRB = 1 << 6;
    public static byte VLRF = 1 << 7;
    //以上为体素为实点的位标记
    public static Int16Triple[] PointIndexToPointDelta = new Int16Triple[8]
    {
        new Int16Triple(0, 1, 1 ),
        new Int16Triple(0, 1, 0 ),
        new Int16Triple(0, 0, 0 ),
        new Int16Triple(0, 0, 1 ),
        new Int16Triple(1, 1, 1 ),
        new Int16Triple(1, 1, 0 ),
        new Int16Triple(1, 0, 0 ),
        new Int16Triple(1, 0, 1 )
    };//体元内每个体素相对基准体素坐标的偏移
    public static byte[] PointIndexToFlag = new byte[8]
    {
        VULF,
        VULB,
        VLLB,
        VLLF,
        VURF,
        VURB,
        VLRB,
        VLRF
    };//每个体素对应的位标记
    public static int[,] EdgeIndexToEdgeVertexIndex = new int[12, 2]
    {
        {0,1}, {1,2}, 
        {2,3},{3,0},
        {4,5},{5,6}, 
        {6,7}, {7,4},
        {0,4}, {1,5}, 
        {2,6}, {3,7}
    };//每个边对应的两顶点体素的索引
    public static Int16Quad[] CubeEdgeMapTable = new Int16Quad[12]
    {
        new Int16Quad(0,1,0,1),
        new Int16Quad(0,0,0,0),
        new Int16Quad(0,0,0,1),
        new Int16Quad(0,0,1,0),

        new Int16Quad(1,1,0,1),
        new Int16Quad(1,0,0,0),
        new Int16Quad(1,0,0,1),
        new Int16Quad(1,0,1,0),

        new Int16Quad(0,1,1,2),
        new Int16Quad(0,1,0,2),
        new Int16Quad(0,0,0,2),
        new Int16Quad(0,0,1,2),
    };


    protected BitMap3d bmp;
    protected int d;
    protected int h;
    protected int w;
    protected int wh;
    public MCProcessor(BitMap3d bitmap)
    {
        this.bmp = bitmap;
    }
    public Mesh GenerateSurface()
    {
        d = bmp.depth;
        h = bmp.height;
        w = bmp.width;
        wh = w * h;
        Int16Triple[] temp = new Int16Triple[8];
        Mesh m = new Mesh();
        OriginalTriangle[] tempTriangles = new OriginalTriangle[6];
        MCTriangleNetHashTable hash = new MCTriangleNetHashTable(0, 0, w, h);

        for (int k = 0; k <= d - 1; k++)
        {
            for (int j = 0; j <= h - 1; j++)
            {
                for (int i = 0; i <= w - 1; i++)
                {
                    byte value = GetConfig(temp, bmp, i, j, k);
                    if (value == 0 || value == 255)
                        continue;
                    int tcount = ExtractTriangles(temp, value, i, j, k, tempTriangles);
                    for (int tindex = 0; tindex < tcount; tindex++)
                    {
                        MergeTriangleIntoMesh(m, hash, tempTriangles[tindex]);
                    }
                }
            }
            hash.IncreaseIndex();
        }
        return m;
    }

    private byte GetConfig(Int16Triple[] temp, BitMap3d flagsMap, int indexInWidth, int indexInHeight, int indexInDepth)
    {
        byte value = 0;
        for (int pi = 0; pi < 8; pi++)
        {
            temp[pi].X = indexInWidth + PointIndexToPointDelta[pi].X;
            temp[pi].Y = indexInHeight + PointIndexToPointDelta[pi].Y;
            temp[pi].Z = indexInDepth + PointIndexToPointDelta[pi].Z;
            if (temp[pi].X < w && temp[pi].X >= 0
                && temp[pi].Y < h && temp[pi].Y >= 0
                && temp[pi].Z < d && temp[pi].Z >= 0
                && IsInsideIsoSurface(temp[pi].X,temp[pi].Y,temp[pi].Z))
            {
                value |= PointIndexToFlag[pi];
            }
        }
        return value;
    }

    private int ExtractTriangles(Int16Triple[] temp, byte value, int indexInWidth, int indexInHeight, int indexInDepth, OriginalTriangle[] result)
    {
        int tcount = 0;
        if (MCTable.TriTable[value, 0] != -1)
        {
            int index = 0;
            while (MCTable.TriTable[value, index] != -1)
            {
                int e0index = MCTable.TriTable[value, index];
                int e1index = MCTable.TriTable[value, index + 1];
                int e2index = MCTable.TriTable[value, index + 2];
                result[tcount] = new OriginalTriangle(indexInWidth,  indexInHeight, indexInDepth,e0index,e1index,e2index);
                tcount++;
                index += 3;
            }
        }
        return tcount;
    }

    private void MergeTriangleIntoMesh(Mesh mesh, MCTriangleNetHashTable hashMap, OriginalTriangle ot)
    {
        int e0i= CubeEdgeMapTable[ot.E0].D;
        int p0x = ot.CellCoord.X + CubeEdgeMapTable[ot.E0].A;
        int p0y = ot.CellCoord.Y + CubeEdgeMapTable[ot.E0].B;
        int p0z = ot.CellCoord.Z + CubeEdgeMapTable[ot.E0].C;


        int e1i = CubeEdgeMapTable[ot.E1].D;
        int p1x = ot.CellCoord.X + CubeEdgeMapTable[ot.E1].A;
        int p1y = ot.CellCoord.Y + CubeEdgeMapTable[ot.E1].B;
        int p1z = ot.CellCoord.Z + CubeEdgeMapTable[ot.E1].C;


        int e2i = CubeEdgeMapTable[ot.E2].D;
        int p2x = ot.CellCoord.X + CubeEdgeMapTable[ot.E2].A;
        int p2y = ot.CellCoord.Y + CubeEdgeMapTable[ot.E2].B;
        int p2z = ot.CellCoord.Z + CubeEdgeMapTable[ot.E2].C;


        int p0i;
        int p1i;
        int p2i;
        int index = 0;
        index = hashMap.GetHashValue(p0x, p0y, p0z,e0i);
        if (index == -1)
        {
            Point3d interp = GetIntersetedPoint(ot.CellCoord.X, ot.CellCoord.Y, ot.CellCoord.Z, ot.E0);
            p0i = mesh.AddVertex(interp);
            hashMap.SetHashValue(p0x, p0y, p0z,e0i,p0i);
        }
        else
        {
            p0i = index;
        }

        index = hashMap.GetHashValue(p1x, p1y, p1z,e1i);
        if (index == -1)
        {
            Point3d interp = GetIntersetedPoint(ot.CellCoord.X, ot.CellCoord.Y, ot.CellCoord.Z, ot.E1);
            p1i = mesh.AddVertex(interp);
            hashMap.SetHashValue(p1x, p1y, p1z,e1i ,p1i);
        }
        else
        {
            p1i = index;
        }

        index = hashMap.GetHashValue(p2x, p2y, p2z,e2i);
        if (index == -1)
        {
            Point3d interp = GetIntersetedPoint(ot.CellCoord.X, ot.CellCoord.Y, ot.CellCoord.Z, ot.E2);
            p2i = mesh.AddVertex(interp);
            hashMap.SetHashValue(p2x, p2y, p2z,e2i ,p2i);
        }
        else
        {
            p2i = index;
        }

        Triangle t = new Triangle(p0i, p1i, p2i);
        mesh.AddFace(t);
    }

    protected virtual Point3d GetIntersetedPoint(int cx,int cy,int cz, int ei)
    {
        int p0i = EdgeIndexToEdgeVertexIndex[ei, 0];
        int p1i = EdgeIndexToEdgeVertexIndex[ei, 1];

        int p0X = cx+PointIndexToPointDelta[p0i].X;
        int p0Y = cy + PointIndexToPointDelta[p0i].Y;
        int p0Z = cz + PointIndexToPointDelta[p0i].Z;

        int p1X = cx + PointIndexToPointDelta[p1i].X;
        int p1Y = cy + PointIndexToPointDelta[p1i].Y;
        int p1Z = cz + PointIndexToPointDelta[p1i].Z;
           
        return new Point3d((p0X+p1X)/2.0f,(p0Y+p1Y)/2.0f,(p0Z+p1Z)/2.0f);
    }

    protected virtual bool IsInsideIsoSurface(int x,int y,int z)
    {
        return bmp.data[x+ w * y + wh * z] == BitMap3d.WHITE;
    }

    protected virtual bool InRange(int x, int y, int z)
    {
            if (x < w && x >= 0
                && y < h && y >= 0
                && z < d && z >= 0)
            {
                return true;
            }
            return false;
    }
}

 

 

效率对比

　　使用用Phantom数据，对其抽取MC/SMC等值面，其中MC/SMC算法分别采用堆砌二维数组与本文的设计，其效率对比如下表所示。

算法

MC(堆砌)

MC(本文)

SMC(堆砌)

SMC(本文)

时间

10211ms

6772ms

8235ms

5104ms

 

工程下载

　　采用此方法实现的算法代码可在如下地址下载：

　　MC：https://github.com/chnhideyoshi/OctreeBaseSimplifiedMarchingCubes/tree/master/MarchingCubes

　　SMC：https://github.com/chnhideyoshi/OctreeBaseSimplifiedMarchingCubes/tree/master/SimplifiedMarchingCubes

　　博主注：在项目：https://github.com/chnhideyoshi/OctreeBaseSimplifiedMarchingCubes增加了C++版本的MC/SMC算法实现。具体项目目录为：

　　MC(C++)：https://github.com/chnhideyoshi/OctreeBaseSimplifiedMarchingCubes/tree/master/MarchingCubesCp

　　SMC(C++)：https://github.com/chnhideyoshi/OctreeBaseSimplifiedMarchingCubes/tree/master/SimplifiedMarchingCubesCp

 

　　爬网的太疯狂了，转载本文要注明出处啊：http://www.cnblogs.com/chnhideyoshi/

posted on 2014-01-01 11:49  Jumanco&Hide  阅读(877)  评论(0)  编辑  收藏  举报