chnhideyoshi

摘要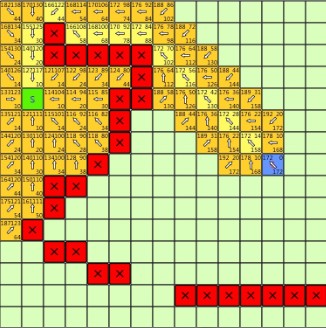： 继上一篇三角网格Dijkstra寻路算法之后，本篇将继续介绍一种更加智能，更具效率的寻路算法—A*算法，本文将首先介绍该算法的思想原理，再通过对比来说明二者之间的相同与不同之处，然后采用类似Dijkstra方式实现算法，算法利用了二叉堆数据结构，最后再通过一些小实验的效果展示其寻路效果。 阅读全文

摘要： 学过数据结构的人都应该知道Dijkstra算法，这是最为经典的带权图寻路算法。其主要特点是以起始点为中心向外层层扩展，直到扩展到终点为止。Dijkstra算法能得出最短路径的最优解，但由于它遍历计算的节点很多，所以效率低。而之后要介绍的A*算法也是在此基础上的一个启发式的改良，能够有效的减少计算遍历节点的个数。各种数据结构书和网上都有对Dijkstra算法的讲解与代码实现，不过少有详细对比二者程序结构区别的文章，而且部分文章的实现虽然简练但不宜理解，因此本文采用从一个较为形象的思路去理解算法，实现代码不求简练和高效，但求通俗易懂，并且利用了面向对象的思路去实现这一算法和A*算法。文章写的比较长，希望能覆盖到所有在实现该算法过程中可能产生疑惑的点，但愿对想了解或者回顾这个算法的人有所帮助。img src="http://images.cnblogs.com/cnblogs_com/chnhideyoshi/561079/o_QQ%e6%88%aa%e5%9b%be20140316214407.jpg" class="desc_img" style="width:120px;height 阅读全文

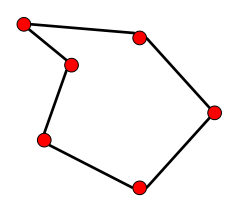摘要： 近期遇到一个计算几何问题，需要从点集中重建一个合理的几何形状。这个问题既有二维的也有三维的，二维的情况相对简单一点，即给出平面区域的一系列散点，求出一定程度上反映这些散点轮廓的平面多边形，给出边的连接方式即可。 阅读全文

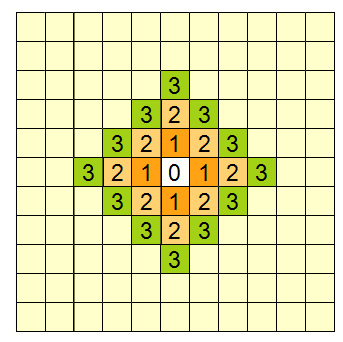摘要： 对图像处理有所了解的人都知道图像的形态学处理里最为基础的膨胀和腐蚀算法。二值图像即只有黑白两种颜色组成的图像，一般的白色为内容，黑色为背景。其实简单点理解二值图像的膨胀与腐蚀，腐蚀即是删除对象边界某些像素，也就是让白色的区域瘦一圈；而膨胀则是给图像中的对象边界添加像素，即让白色的区域胖上一圈。而这个“圈”的大小，则是由参数来指定的。下面的表展示了一幅图像经过膨胀和腐蚀算法的结果。可以看出膨胀让白色区域大了一圈，白色区域若有较小的黑色洞，则洞被填上。 阅读全文

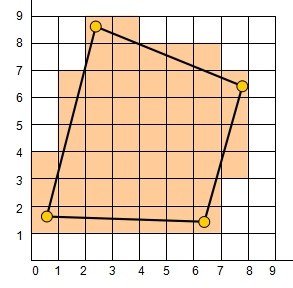摘要： 学计算机的人往往都比较清楚图形和图像的区别，而且往往能够从数据结构的角度理解这两者的区别，一般来说，图形是由几何空间中的基本图元所组成，表现为用外部轮廓线条勾勒成的矢量图。例如由计算机绘制的直线、圆、矩形、曲线、图表等。而图像是由扫描仪、摄像机等输入设备捕捉实际的画面产生的数字图像，是由像素点阵构成的位图。例如在二维几何空间中，同样是为了表述一个四边形，从图形的角度去看，需要提供四个顶点的坐标作为基本图元，然后提供一个画线的指令，将四个顶点按顺序提供出来。而从图像的角度看，一个四边形需要映射为一个特定分辨率位图上的像素集合。 阅读全文

摘要： 某个图像处理的任务需求被转化为一个寻找图像局部最大值的问题，例如下面的图像是一段来自医学投影的组织影像，其中用肉眼能够辨识出一些灰度值比较大的团块，这些团块都是代表着一定医学含义的组织。需求是找出类似这种团块的个数。 阅读全文

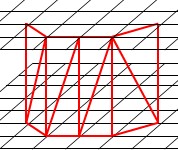摘要： 在之前的关于MC算法与SMC算法的博文中介绍了算法的实现，文章主要围绕算法的核心问题，即三角片如何产生的问题进行了详细的描述。但由于实际应用中需要的等值面Mesh数据不是三角片的简单并集，所以需要进行所谓的顶点焊接(Vertex Welding)来生成正确的拓扑结构以反应三角片之间的共用顶点关系。顶点焊接，简单的说就是把三角片中重合的顶点算作一个顶点加入顶点集。 阅读全文

摘要： 网格平滑属于数字几何处理领域的问题，计算机图形学和计算机辅助设计中，用多边形网格可以表示复杂的三维实体。随着三维扫描和曲面重建技术的发展，得到这些实体表面的多边形网格表示已经不是难事，但所得到的表面往往包含含噪声。在形状设计领域，在散乱点拟合和光滑形伏、纹理映射等应用领域，都有对平滑曲面的极大需求。故产生了网格平滑这一个研究点。 阅读全文

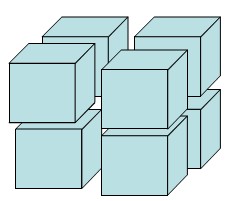摘要： 对于网格生成这个主题，之前的网格生成系列的三篇博客文章分别介绍了MC算法，SMC算法以及Cuberille算法三种方法。同时还有一篇介绍网格生成与种子点生长算法高效结合的算法。本篇文章继续这一主题，介绍采用八叉树结构来进行网格生成的算法，这个算法并不是独立于之前介绍的算法，而是基于了SMC算法，同时也采纳了一些MC算法范畴内的思想。换句话说，就是使用八叉树对上述网格生成进行改良，从而进一步减少网格的规模。 阅读全文

摘要： 这是本博客网格生成算法系列的第三篇，第一篇里面介绍了最为流行的MarchingCubes算法，第二篇中使用新三角形表来对MC算法进行了简化改进，形成了SMC算法。而这篇将介绍一种新的不同与MC算法思路的新网格生成算法，叫做Cuberille法，这种算法的思想相比MC算法要简单，更加易于实现。 阅读全文

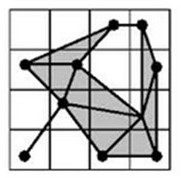摘要： 本篇接顶点去重那一篇，继续使用哈希表来实现网格算法。这次介绍的是一种比较简单的网格简化算法，叫做顶点聚簇。 阅读全文

摘要： 本篇接上一篇继续介绍网格生成算法，同时不少内容继承自上篇。上篇介绍了经典的三维图像网格生成算法MarchingCubes，并且基于其思想和三角形表实现了对样例数据的网格构建。本篇继续探讨网格生成算法，并且在MC的基础上进行进一步的简化和改进，形成Simple Marching Cubes（简称SMC算法）。本篇主要介绍SMC算法的思路以及与MC算法的对比。同时也介绍如何在MC三角形表的基础上生成SMC三角形表。 阅读全文

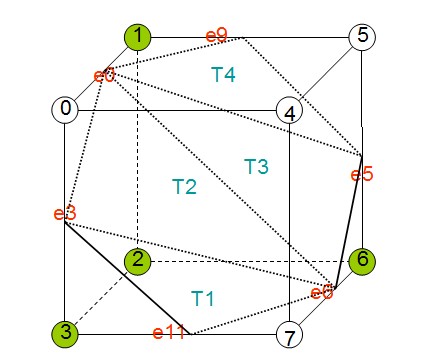摘要： 之前的博文已经完整的介绍了三维图像数据和三角形网格数据。在实际应用中，利用遥感硬件或者各种探测仪器，往往很容易获得表征现实世界中物体的三维图像。比如利用CT机扫描人体得到人体断层扫描图像，就是一个表征人体内部组织器官形状的一个三维图像。其中的感兴趣的组织器官通过体素的颜色和背景加以区别。 阅读全文

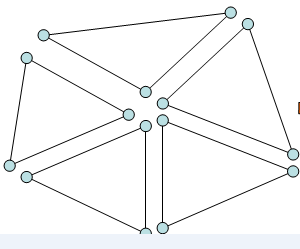摘要： 之前的文章讨论了三角网格，顶点焊接这个主题是由三角网格建模衍生出来的。简单点说，顶点焊接又可以叫做“顶点去重”，就是要在Mesh中去除重复的顶点。由之前的介绍Mesh的文章可以知道，Mesh实际上就是顶点的集合+三角形的集合，其中三角形是由三个指向顶点集合的索引表示的。 阅读全文

摘要： 本篇继续介绍Mesh相关的一些算法，包括计算面法向，邻接面，点法向，邻接点，以及拉普拉斯平滑算法，同时丰富了Mesh的成员。 阅读全文

摘要： 三角网格是多边形网格的一种，多边形网格又被称为“Mesh”，是计算机图形学中用于为各种不规则物体建立模型的一种数据结构。现实世界中的物体表面直观上看都是由曲面构成的；而在计算机世界中，由于只能用离散的结构去模拟现实中连续的事物。所以现实世界中的曲面实际上在计算机里是由无数个小的多边形面片去组成的。比如下图的形状，在计算机渲染后由肉眼看是十分平滑的曲面，而实际上，计算机内部使用了大量的小三角形片去组成了这样的形状。这样的小面片的集合就被称作Mesh。Mesh既可以由三角形组成，也可以由其他平面形状如四边形，五边形等组成； 阅读全文

摘要： 首先对于任何一个二维图像B，加载入内存后都能看作一个二维像素数组。假如是一张8位图像，它的每个像素值就是一个0~255，也就是一个像素的数值。假设它的长和宽分别为width和height，那么这个图像用byte B[height,width]（c#二维数组）或者用unsigned char B[height][width]（C++二维数组）来表示就非常的恰当。推而广之，假如是一个长宽高分别是width、height和depth的三维图像，那么就可以采用三维数组来byte B[depth,height,width]（C#）或者unsigned char B[depth][height][width]（C++）来表示。 阅读全文