Max Sum(动态规划)
原创
http://acm.hdu.edu.cn/showproblem.php?pid=1003
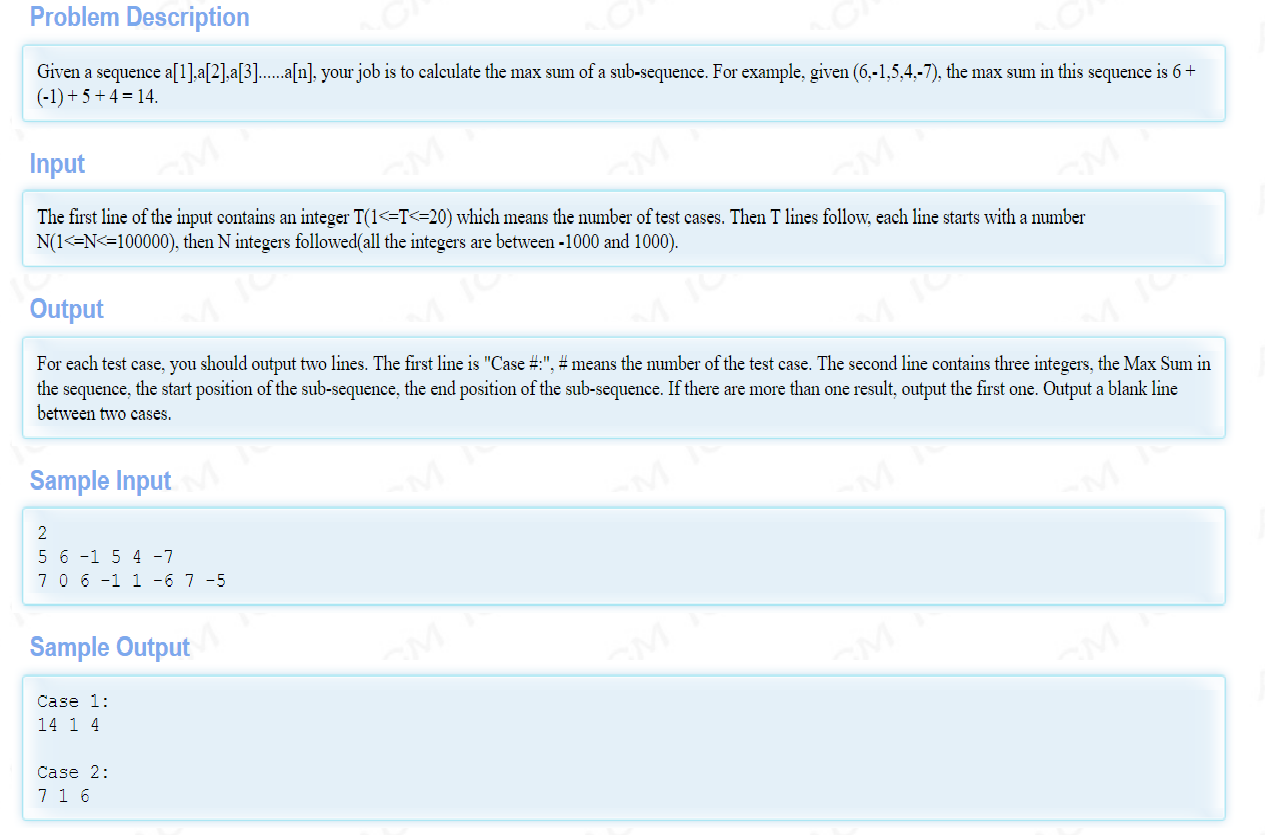
题目要求求出一个序列里面的最大序列和，序列要求是连续的，给出最大序列和，序列首元素下标和尾元素下标，按特定的格式输出。
解题思路：
动态规划，我们可以将所有序列按以序列中的元素a[i](i=1~n)结尾进行分类，比如：
以a[1]结尾的序列有：a[1]
以a[2]结尾的序列有：a[1]a[2],a[2]
以a[3]结尾的序列有：a[1]a[2]a[3],a[2][3],a[3]
......
这样所有序列都会包含在其中，一共被分为n大组，每大组里面包含许多小序列，从每大组里面选出最大的序列和，这样会选出n个
序列和，再从n个序列和中选出最大的就是题目要求的最大序列和了。
动态规划公式演算：
之前说过有n大组，用dp[]存储从每大组中选出来的最大序列和，其中
dp[1]=a[1]
dp[2]=max(a[1]a[2],a[2]),即从两个序列里面选出序列和最大的，既然只需要比较序列和，两个数比较大小，两个数同时减去一
个相同的数不影响比较，那么两个序列都先把元素a[2]减去，这样就成了dp[2]=max(dp[1]+a[2],a[2])。
dp[3]=max(a[1]a[2]a[3],a[2][3],a[3]),写成max(a[1]a[2]+a[3],a[2]+[3],0+a[3])更容易理解动态规划思想,3个序列都先把
a[3]提出变成max(a[1]a[2],a[2],0),再变成max(max(a[1]a[2],a[2]),0)，三个数比较，可以先比较其中2个，再和第三个比较，
可以发现max(a[1]a[2],a[2])就是dp[2]，所以max(a[1]a[2],a[2],0)就是max(dp[2],0),加回a[3]，max(dp[2]+a[3],a[3])。
所以我们可以轻而易举的按顺序求出n大组的序列和，然后再从n个序列和中求出最大的。
关于求最大序列和的首尾元素索引：
我们在求某个dp[i]的时候，代表目前是从以a[i]结尾的序列和中求出序列和最大的存入dp[i]中，所以尾元素可以得知。
尾元素得到，可以往回找到首元素。
Java AC
1 import java.util.*; 2 3 public class Main { 4 5 public static void main(String[] args) { 6 Scanner reader=new Scanner(System.in); 7 int T=reader.nextInt(); 8 int count=1; 9 while(T>0) { 10 int N=reader.nextInt(); 11 int a[]=new int[N+1]; 12 for(int i=1;i<=N;i++) { 13 a[i]=reader.nextInt(); 14 } 15 int dp=a[1]; 16 int sum_Max=dp; 17 int start=1; 18 int end=1; 19 for(int i=2;i<=N;i++) { 20 dp=dp+a[i]>a[i]?(dp+a[i]):a[i]; //动态存储以a[1]~a[n]结尾的序列组的最大序列和 21 if(dp>sum_Max) { 22 sum_Max=dp; 23 end=i; //结尾索引 24 } 25 } 26 //寻找开头索引 27 int sum=0; 28 for(int i=end;i>=1;i--) { 29 sum+=a[i]; 30 if(sum==sum_Max) { 31 start=i; 32 //这里不能break,当序列中存在多个序列具有同样的最大序列和,题目要求输出第一个被找到的序列 33 } 34 } 35 System.out.println("Case "+count+":"); 36 System.out.println(sum_Max+" "+start+" "+end); 37 if(T!=1) { 38 System.out.println(); 39 } 40 T--; 41 count++; 42 } 43 } 44 45 }
21:21:39
2018-08-19
