Dijkstra
原创
Dijkstra算法用于求最短路径。
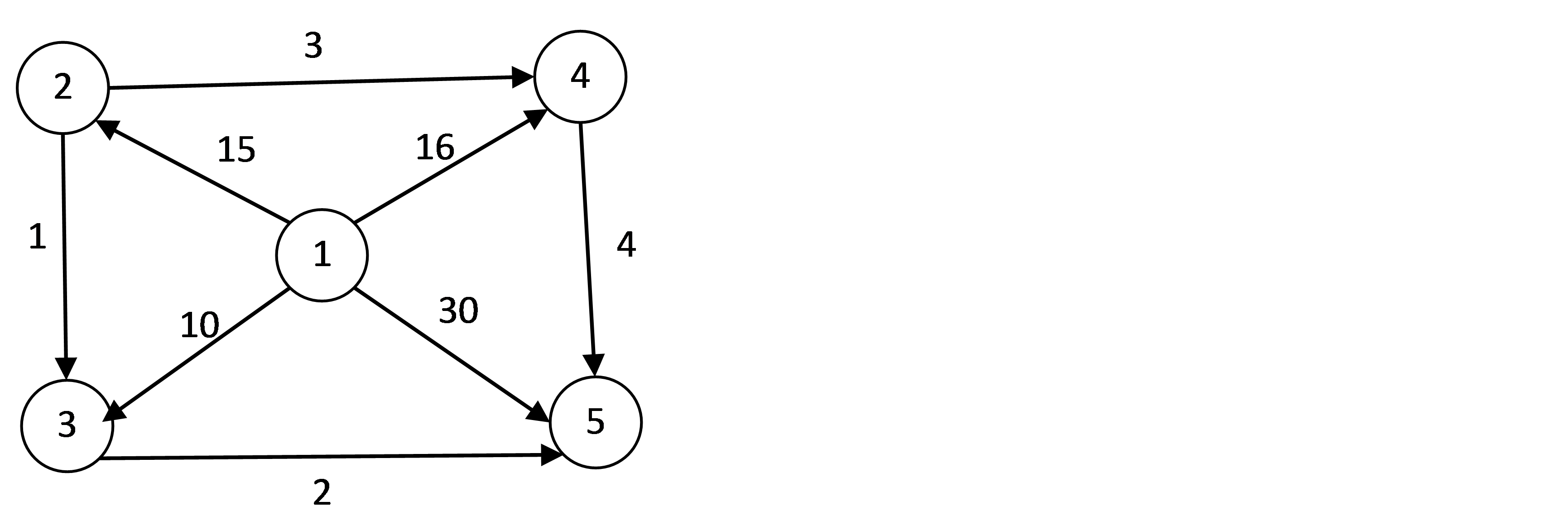
用邻接矩阵存储图，若求1到其余顶点的最短路径，用数组dis存储1到其余顶点的最短路径。
dis初始化即顶点1到其余顶点的初始距离，不直接相连的即为无穷大，上图中dis初始化为0/15/10/16/30。
接下来从数组dis中选出一个最小值，上图中为10（0为到自身的距离），则1到3的最短距离即为10，理解
这一点很重要，因为与1直接相连的点中距离最小的顶点是3，距离是10，若通过其余顶点其余路径到达3，距离
都会大于10，所以1到顶点3的最短路径已经确认了，以后无需更新。
确认了这条最短路径，比较好好利用它，看看1通过这条最短路径能不能缩短1到其余顶点的距离，比如上图
中1到5的距离为30，但是通过最短路径1到3再到5就能缩短1都5的距离，其余边也要一一判断缩小，此过程称为“松弛”。
Dijkstra求最短路径的基本步骤如下：
1. 将所有的顶点分为两部分：已知最短路径的顶点集合P和未知最短路径的顶点集合Q。最开始，已知最短路径
的顶点集合P中只有源点一个顶点。我们这里用一个book数组来记录哪些点在集合P中。例如对于某个顶点i，如
果book[i]为1则表示这个顶点在集合P中，反之，则在集合Q中。
2. 设置源点s到自己的最短路径为0即dis[s]=0.若存在有源点能直接到达的顶点i，则把dis[i]设为matrix[s][i],
matrix为邻接矩阵。同时把所有其他（源点不能直接到达的）顶点的最短路径设为∞。
3. 在集合Q的所有顶点中选择一个离源点s最近的顶点u（即dis[u]最小）加入到集合P中。并考察所有以点u为起点的边，
对每一条边进行松弛操作。例如存在一条从u到v的边，那么可以通过将边u-v添加到尾部来拓展一条从s到v的路径，这
条路径的长度是dis[u]+e[u][v]。如果这个值比目前已知的dis[v]的值要小，我们可以用新值来替代当前dis[v]中的值。
4. 重复第3步，如果集合Q为空，算法结束。最终dis数组中的值就是源点到所有顶点的最短路径。
1 import java.util.*; 2 3 public class Dijkstra { 4 5 static int v; //顶点 6 static int e; //边 7 static int aim; //aim与其余顶点的最短路径 8 static int matrix[][]; //邻接矩阵 9 static int book[]; //标记数组 10 static int dis[]; //存储与其他顶点的距离 11 static int min=99999; 12 static int inf=99999; 13 14 public static void main(String[] args) { 15 Scanner reader=new Scanner(System.in); 16 v=reader.nextInt(); 17 e=reader.nextInt(); 18 aim=reader.nextInt(); 19 matrix=new int[v+1][v+1]; //从1开始编号 20 book=new int[v+1]; 21 dis=new int[v+1]; 22 //矩阵初始化 23 for(int i=1;i<=v;i++) { 24 book[i]=0; 25 for(int j=1;j<=v;j++) { 26 if(i==j) { 27 matrix[i][j]=0; 28 } 29 else { 30 matrix[i][j]=inf; 31 } 32 } 33 } 34 book[aim]=1; //求aim到其余顶点的距离 35 //读入边 36 for(int i=1;i<=e;i++) { 37 int first_City=reader.nextInt(); 38 int second_City=reader.nextInt(); 39 int value=reader.nextInt(); 40 matrix[first_City][second_City]=value; //有向图 41 } 42 //数组dis初始化 43 for(int i=1;i<=v;i++) { 44 dis[i]=matrix[aim][i]; 45 } 46 for(int i=1;i<=v-1;i++) { //循环v-1次，每次确认一个顶点 47 int u=-1; 48 min=inf; 49 //寻找距离aim最近的点 50 for(int j=1;j<=v;j++) { 51 if(book[j]==0 && dis[j]<min) { 52 min=dis[j]; 53 u=j; 54 } 55 } 56 if(u==-1) { 57 break; 58 } 59 book[u]=1; //确认顶点u 60 //松弛 61 for(int z=1;z<=v;z++) { 62 if(matrix[u][z]<inf) { 63 if(dis[z]>dis[u]+matrix[u][z]) { //更新距离 64 dis[z]=dis[u]+matrix[u][z]; 65 } 66 } 67 } 68 } 69 for(int i=1;i<=v;i++) { 70 System.out.print(dis[i]+" "); 71 } 72 } 73 74 }
14:32:02
2018-07-29
