Floyd-Warshall求图中任意两点的最短路径
原创
除了DFS和BFS求图中最短路径的方法,算法Floyd-Warshall也可以求图中任意两点的最短路径。
从图中任取两点A、B,A到B的最短路径无非只有两种情况:
1:A直接到B这条路径即是最短路径(前提是存在此路径);
2:A先通过其他点,再由其他点到B。
我们并不知道A是否需要通过其他点间接到达B,所以只能比较,用A到B的直接路径和A先通过其他点
再间接到达B的路径长度进行比较,然后更新为较小值。
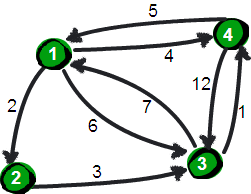
上图中若要求顶点4到顶点3的最短路径,可以比较顶点4直接到3的路径和顶点4先到1,再到3的路径。
更新为最小值,此时邻接矩阵matrix[4][3]存储的即为借用了顶点1后4到3的最短路径;然后再借用了1的
基础上再借用顶点2,此时再次比较matrix[4][3]和matrix[4][2]+matrix[2][3],更新为最小值;比较完
毕后matrix[4][3]乃存储了最短路径,求其他任意两点也是如此。
总结一下,求图中任意两点的最短路径,通过比较一次取一个其他顶点间接到达的最短路径和直接路径
进行比较,更新为最小值即可。
import java.util.*; public class Floyd_Warshall { static int v; //顶点 static int e; //边 static int matrix[][]; public static void main(String args[]) { Scanner reader=new Scanner(System.in); v=reader.nextInt(); e=reader.nextInt(); matrix=new int[v+1][v+1]; //编号从1开始 //矩阵初始化 for(int i=1;i<=v;i++) { for(int j=1;j<=v;j++) { if(i==j) { //顶点本身 matrix[i][j]=0; } else { //无穷 matrix[i][j]=99999; } } } //读入边 for(int i=1;i<=e;i++) { int first_City=reader.nextInt(); int second_City=reader.nextInt(); int value=reader.nextInt(); matrix[first_City][second_City]=value; //有向图 } for(int k=1;k<=v;k++) { //只允许经过顶点k for(int i=1;i<=v;i++) { for(int j=1;j<=v;j++) { if(matrix[i][k]+matrix[k][j]<matrix[i][j]) { matrix[i][j]=matrix[i][k]+matrix[k][j]; } } } } for(int i=1;i<=v;i++) { for(int j=1;j<=v;j++) { System.out.print(matrix[i][j]+" "); } System.out.println(); } } }
测试用例:
输入:
4 8
1 2 2
2 3 3
3 4 1
4 3 12
1 3 6
3 1 7
1 4 4
4 1 5
输出:
0 2 5 4
9 0 3 4
6 8 0 1
5 7 10 0
12:30:24
2018-07-28



 浙公网安备 33010602011771号
浙公网安备 33010602011771号