希尔伯特曲线——第八届蓝桥杯C语言B组(国赛)第三题
原创
标题:希尔伯特曲线
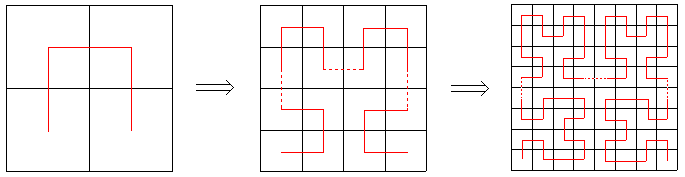
希尔伯特曲线是以下一系列分形曲线 Hn 的极限。我们可以把 Hn 看作一条覆盖 2^n × 2^n 方格矩阵的曲线,曲线上一共有 2^n × 2^n 个顶点(包括左下角起点和右下角终点),恰好覆盖每个方格一次。
[p1.png]
Hn(n > 1)可以通过如下方法构造:
1. 将 Hn-1 顺时针旋转90度放在左下角
2. 将 Hn-1 逆时针旋转90度放在右下角
3. 将2个 Hn-1 分别放在左上角和右上角
4. 用3条单位线段把4部分连接起来
对于 Hn 上每一个顶点 p ,我们定义 p 的坐标是它覆盖的小方格在矩阵中的坐标(左下角是(1, 1),右上角是(2^n, 2^n),从左到右是X轴正方向,从下到上是Y轴正方向),
定义 p 的序号是它在曲线上从起点开始数第几个顶点(从1开始计数)。
以下程序对于给定的n(n <= 30)和p点坐标(x, y),输出p点的序号。请仔细阅读分析源码,填写划线部分缺失的内容。
#include <stdio.h>
long long f(int n, int x, int y) {
if (n == 0) return 1;
int m = 1 << (n - 1);
if (x <= m && y <= m) {
return f(n - 1, y, x);
}
if (x > m && y <= m) {
return 3LL * m * m + f(n - 1, ________________ , m * 2 - x + 1); // 填空
}
if (x <= m && y > m) {
return 1LL * m * m + f(n - 1, x, y - m);
}
if (x > m && y > m) {
return 2LL * m * m + f(n - 1, x - m, y - m);
}
}
int main() {
int n, x, y;
scanf("%d %d %d", &n, &x, &y);
printf("%lld", f(n, x, y));
return 0;
}
注意:只填写划线处缺少的内容,不要填写已有的代码或符号,也不要填写任何解释说明文字等。
(分别称下图三个网格称为A、B、C网格)
#include <stdio.h> long long f(int n, int x, int y) { //(x,y)只是用来判断在哪部分 if (n == 0) return 1; int m = 1 << (n - 1); if (x <= m && y <= m) { //左下角 return f(n - 1, y, x); //返回给上一层的是此点在此层的序号 } if (x > m && y <= m) { //右下角 return 3LL * m * m + f(n - 1,m+1-y, 2 * m - x + 1); // 填空 } if (x <= m && y > m) { //左上角 return 1LL * m * m + f(n - 1, x, y - m); } if (x > m && y > m) { //右上角 return 2LL * m * m + f(n - 1, x - m, y - m); } } int main() { int n, x, y; scanf("%d %d %d", &n, &x, &y); //n为2的指数,(x,y)为顶点坐标 printf("%lld", f(n, x, y)); return 0; } /* 得找出当前层的点对下一层相应点的映射关系 */
答案:m+1-y
要明确的是:每个网格中的1*1的方格都对应曲线上的一个顶点——即使有些1*1的方格内不存在转折点,但也是曲线上的一个顶点。
int m = 1 << (n - 1); /* 左移1位相当于原数*2,左移2位相当于原数*pow(2,2); 所以 m==1*pow(2,n-1); 其实 m存储的就是边长为:pow(2,n) x pow(2,n) 的二分之一的长 比如:输入的 n = 3,网格规模为8x8,则 m==4 */
if (x <= m && y <= m) { //左下角 return f(n - 1, y, x); //返回给上一层的是此点在此层的序号 } if (x > m && y <= m) { //右下角 return 3LL * m * m + f(n - 1,m+1-y, 2 * m - x + 1); // 填空 } if (x <= m && y > m) { //左上角 return 1LL * m * m + f(n - 1, x, y - m); } if (x > m && y > m) { //右上角 return 2LL * m * m + f(n - 1, x - m, y - m); } /* 四个 if()中的 return 返回给上一层都是当前层顶点(x,y)的序号 根据曲线的走势,左下角是序号的第一部分,其实是左上角、右上角、右下角 比如我们要求左上角的顶点序号,所以我们应该要加上左下角的顶点数:1LL*m*m; 要求右下角的顶点序号,要加上前面三部分(左下角、左上角、右上角)的顶点数:3LL * m * m XLL * m * m + f() (X=0/1/2/3,LL 代表长长整型) f()代表的是下一层传过来的点序号 所以 '+' 左边的部分加上右边的部分==(x,y)的序号 */
XLL * m * m + f()中 f()的两个参数的确定:
n-1传递给下一层,方便计算m,这里不解释;
另外两个参数分别对应下一层的(x,y),即用这层的 x’,y‘表示下一层的 x,y ;
左上角、右上角、左下角中的参数容易确定,我们用待定系数法来确定右下角的两个参数;
if (x > m && y <= m) { //右下角 return 3LL * m * m + f(n - 1,m+1-y, 2 * m - x + 1); // 填空 }
由 2 * m - x + 1 可知下一层的 y 和当前层的 x 是相关联的;
所以推测下一层的 x 和当前层的 y 是相关联的;
设当前层的坐标为 (x',y'),下一层的坐标为(x,y);
所以 y = 2 * m - x' + 1;即 x' = 2 * m - y + 1;(用下一层的坐标表示当前层的坐标)
可设 y’ = m*a + b*x + c;由于 m已知,所以可化简为 y' = b*x + F
我们从B、C两图中找出可以带入上式求出未知参数的坐标;
(1,1)——> (8,4)
(2,1)——> (8,3)
(3,1)——> (8,2)
左边的坐标从B图中任意取,右边的坐标要从C图的右下角部分取(我们的目标是右下角);
比如B图中的序号为7的顶点的坐标为(2,4);在C图右下角也找到序号为7的顶点,坐标为(5,3);
将左边坐标的横坐标、右边坐标的纵坐标代入 y' = b*x + F 得:
4=b+F;
3=2b+F;
解得 b = -1,F=5;
所以 m*a+c=5;从 x' 的表达式很容易就可以推测出 F = m + 1;
当然,我这种是不严格的解题方法!
22:31:53
2018-05-08



 浙公网安备 33010602011771号
浙公网安备 33010602011771号