极大极小博弈树的简洁（附Tic-Tac-Toe源码）

简介

极大极小博弈树(Minimax Game Tree)用于编写电脑之间的游戏程序，这类程序由两个游戏者轮流，每次执行一个步骤。当然，所有可能的步骤构成了一个树的结构。例如下面的图就是一个MGT，它表示了Tic-Tac-Toe游戏的前两步所有可能的步骤。

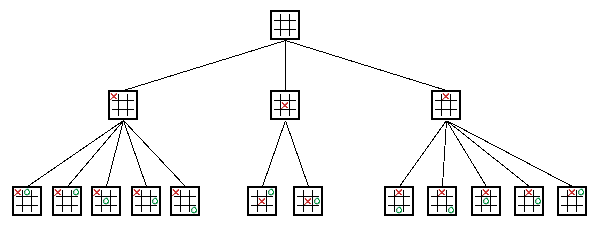
在每一层中的节点通常代表不同游戏者的选择，这两个游戏者通常被称作马克思（MAX）和米恩（Min）。

例如如果第二层是Max turn，则第三层就是Min turn，第二层的每个节点就是Max的choice，它们之间是或的关系，第三层的每个节点就是Min的choice，它们之间是与的关系。根据这个树，Max要做出的选择就让下次Min做出的任意选择都最小，即Minimax这个词的含义，极小化对手的最大收益。所以它不同于Maximin最大化自己的收益。

因为往往一局要下到最后才能分出胜负，而Game Tree上nodes的增长是以指数方式的，比如深蓝（Deep Blue）可以搜索12步，假设各方每步都有10种选择，那么一次的搜索量也有1万亿次，所以对于普通的电脑能够搜索到4步也有1万次了，所以就需要一个评分系统，对局面进行打分，考虑到是双人对战，则评分从负无穷到正无穷。所以马克思就是要找到一个最大的分数，而米恩就是要找到一个最小的分数。

  

例子

下面用一个例子来说明，Tic-Tac-Toe游戏。

其中‘o’代表PC，‘x’代表玩家。

其中有三个主要的函数：

int minSearch( char _board[9] )

int maxSearch( char _board[9] )

int gameState(char _board[9])

分别扮演max和min的角色，寻找最大和最小值，以及一个评分函数。

下面重点说说这个游戏的核心部分，gameState评分函数：

连三          100分

双连二       50分

平局          0分

不分胜负     1

其中如果评分时不分胜负则还会继续搜索，直到找到其他三种状态。

implementation

int gameState(char _board[9])
{
    int state;
    static int table[][3] =
    {
        {0, 1, 2},
        {3, 4, 5},
        {6, 7, 8},
        {0, 3, 6},
        {1, 4, 7},
        {2, 5, 8},
        {0, 4, 8},
        {2, 4, 6},
    };
    char chess = _board[0];
    for (char i = 1; i < 9; ++i)
    {
        chess &= _board[i];
    }
    bool isFull = 0 != chess;
    bool isFind = false;
    for (int i = 0; i < sizeof(table) / sizeof(int[3]); ++i)
    {
        chess = _board[table[i][0]];
        int j;
        for (j = 1; j < 3; ++j)
            if (_board[table[i][j]] != chess)
                break;
        if (chess != empty && j == 3)
        {
            isFind = true;
            break;
        }
    }
    if (isFind)
        //got win or lose
        state = chess == o ? WIN : LOSE;
    else
    {
        if (isFull)
            //all position has been set without win or lose
            return DRAW;
        else
        {
            //finds[0] -> 'o', finds[1] -> 'x'
            int finds[2] = {0, };
            for (int i = 0; i < sizeof(table) / sizeof(int[3]); ++i)
            {
                bool findEmpty = false;
                chess = 0xff;
                int j;
                for (j = 0; j < 3; ++j)
                    if (_board[table[i][j]] == empty && !findEmpty)
                        findEmpty = true;
                    else
                        chess &= _board[table[i][j]];
                if ((chess == o || chess == x) && findEmpty)
                {
                    isFind = true;
                    if (o == chess)
                        ++finds[0];
                    else
                        ++finds[1];
                }
            }
            if (finds[0] > 1 && finds[1] < 1)
                //2 'o' has been founded twice in row, column or diagonal direction
                state = -(INFINITY / 2) * finds[0];
            else if (finds[1] > 1 && finds[0] < 1)
                //2 'x' has been founded twice in row, column or diagonal direction
                state = INFINITY / 2 * finds[1];
            else
                //need to search more.
                state = INPROGRESS;
        }
    }
    return state;
}

 

最后附上源码：https://files.cnblogs.com/chinese-zmm/Tic-Tac-Toe.7z

 

Reference

http://en.wikipedia.org/wiki/Minimax

http://www.cnblogs.com/goodness/archive/2010/05/27/1745756.html