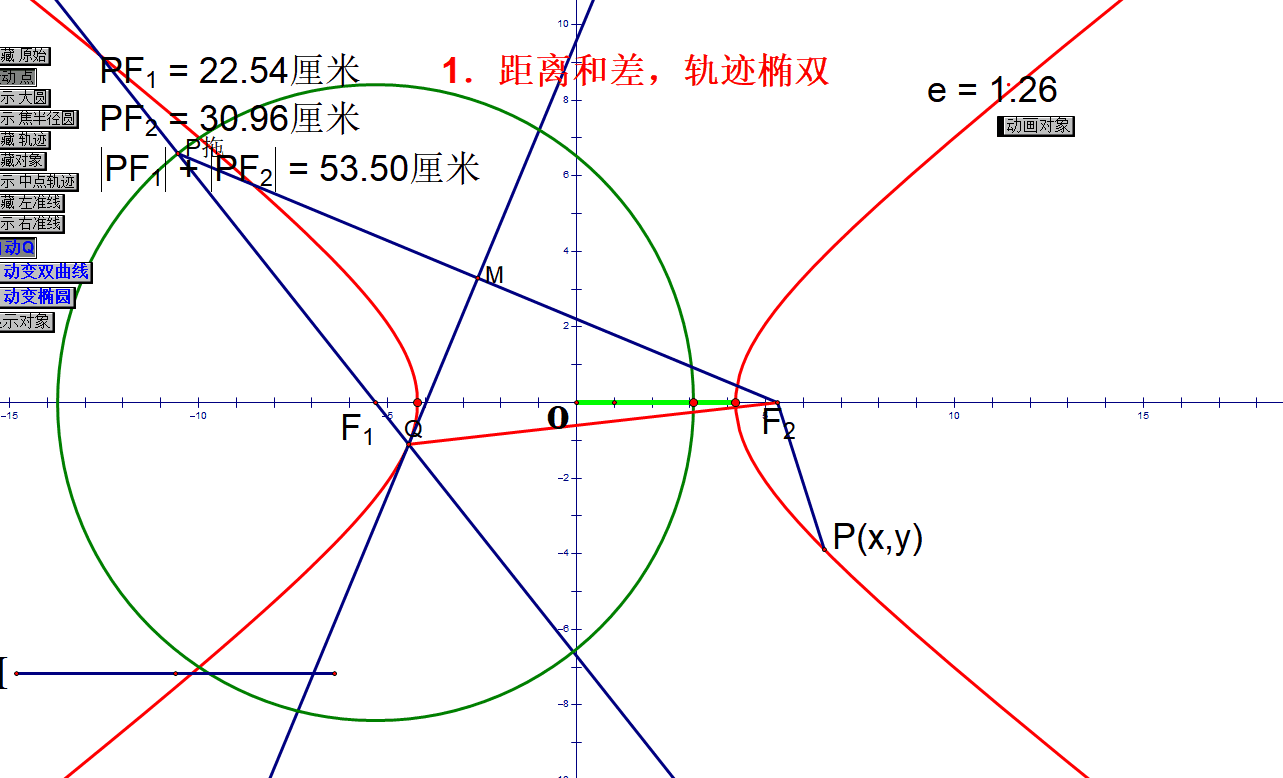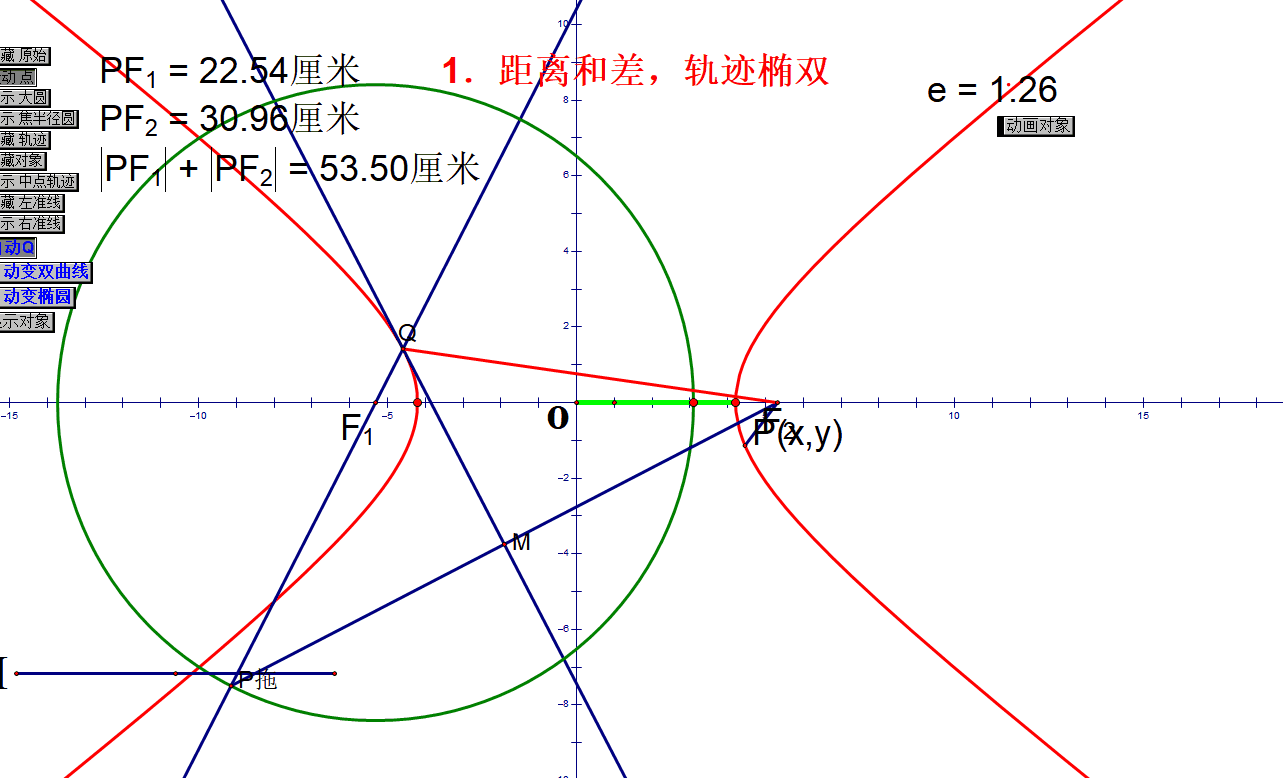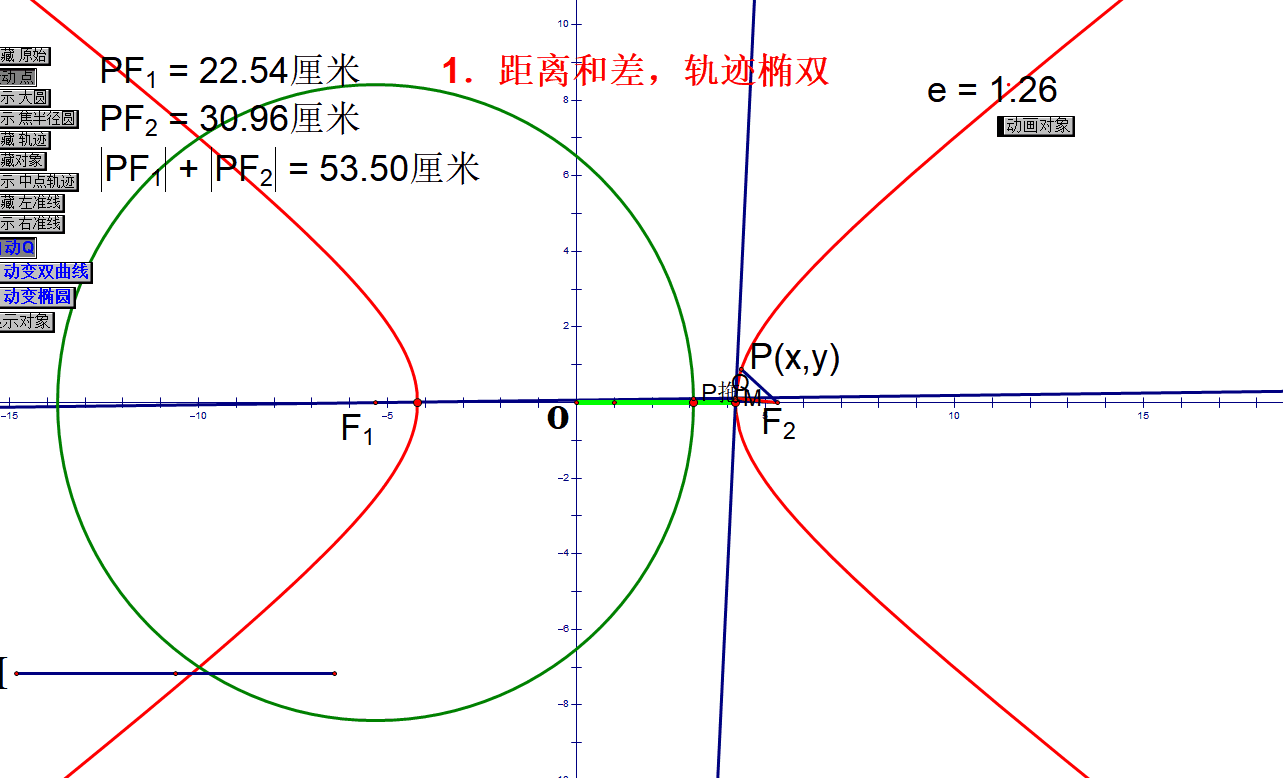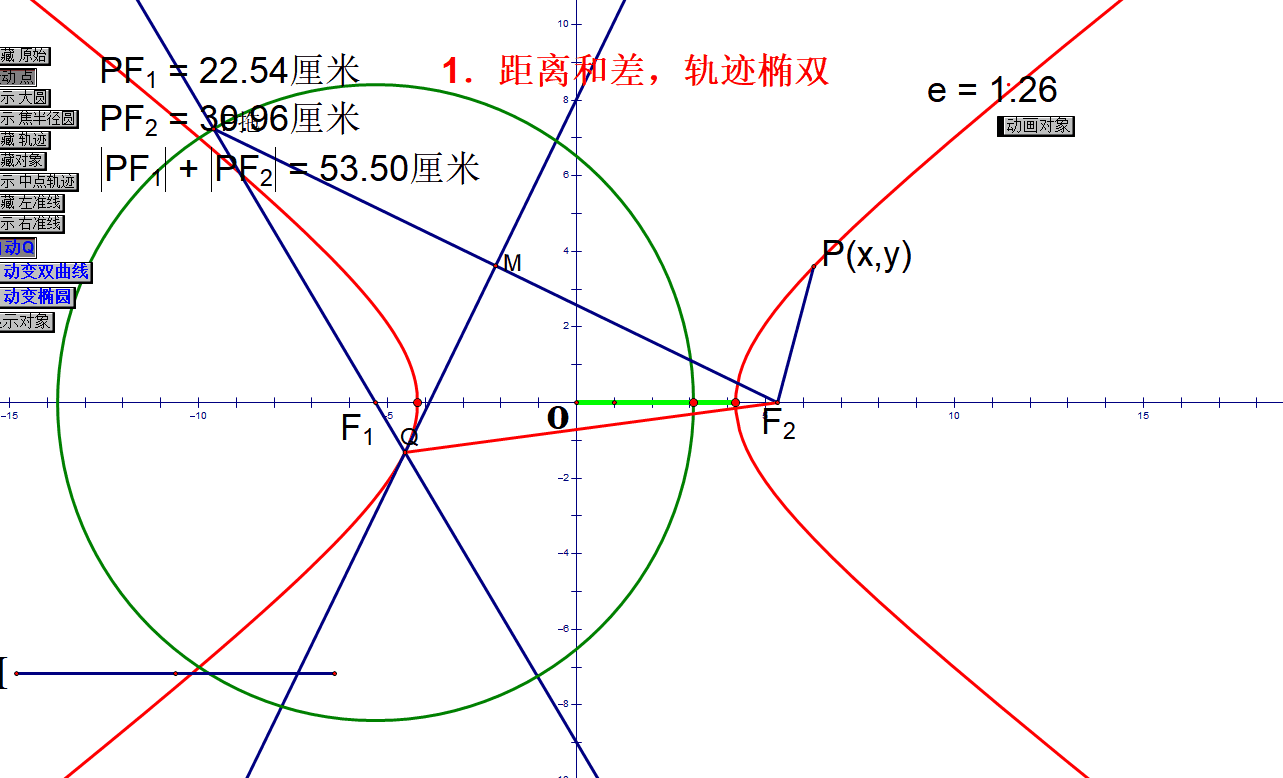
圆锥曲线读书笔记

1.优化解题策略，运算化简要科学，不然过于复杂。不断积累优化。优化到恰到好处，不多也不少，记忆太少不全面，记忆太多人就会混乱。

2.利用本身已经有的几何性质来解题。一般套路，几何关系坐标化。

3.常见的公式，常见的技巧，一定要记住。记住重要的解体模型。挖掘隐含条件，将隐含条件等价为基本结论，解题步骤框架，互为充分必要条件。使用几何画板，绘制直观图像

4. x=my+b  相比于 y=kx+b，可以排除斜率不存在的情况

5.共线问题，可以用极坐标化简。

6.基本知识储备是骨架，例题和习题是血肉，方法是灵魂。

没有哪个模式的题目可以套用所有的考题，遇到新颖，或者更加深刻的，还需要分解和转化为已经掌握的知识点，再加以重组和创造洗的呢解题模式。最终的境界就是 太极张三丰的最高境界，无招胜有招，没有模式就是最好的模式。无论什么题目都能准确快速的转化到已经遇到过的问题。

7.题目分为两类，动态和静态，静态的问题，利用几何关系，一定能求出，动态的是难点，比如求极值，点运动的轨迹。

8.求三角形面积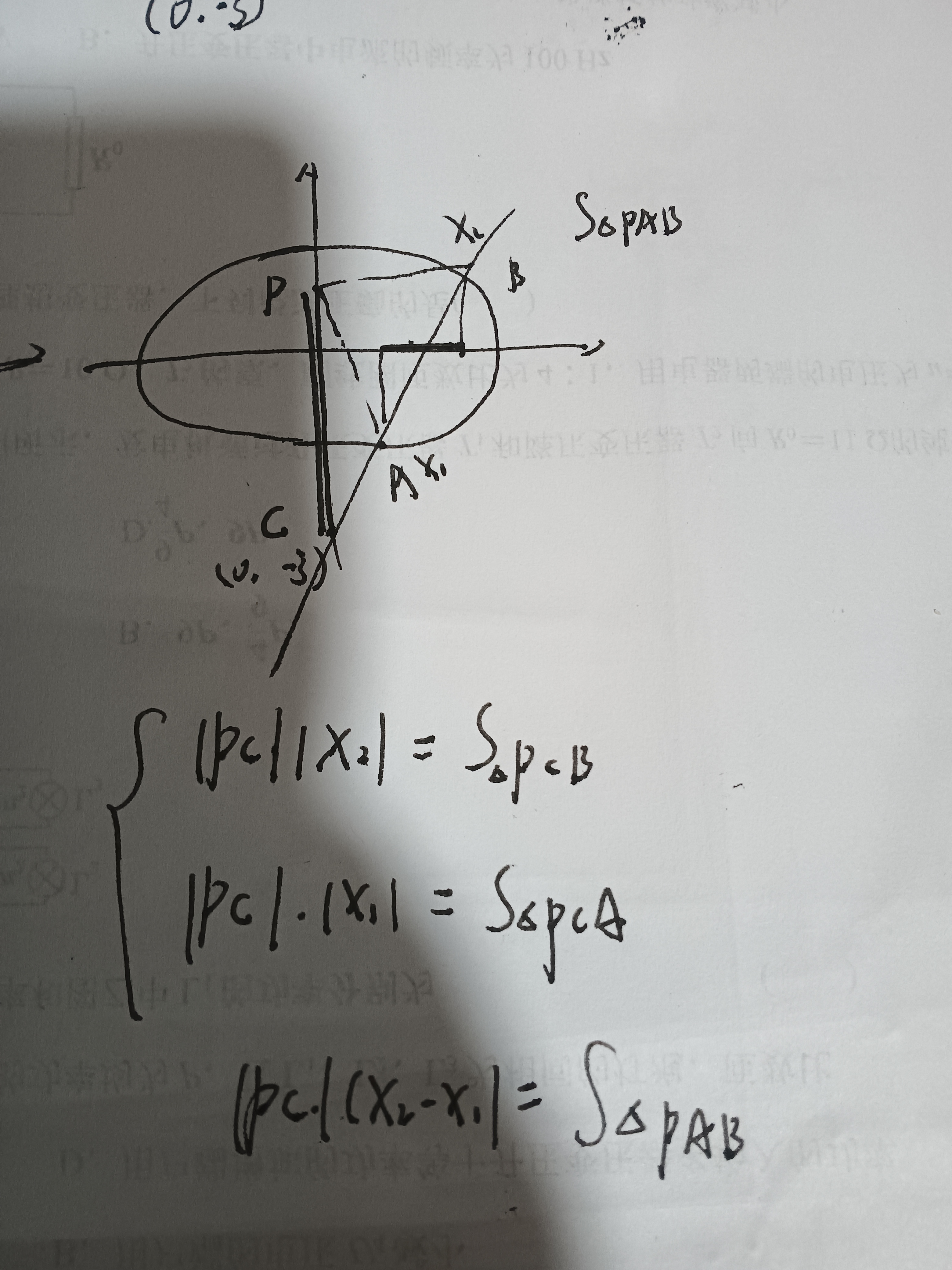

 

9. 圆锥曲线  含有   斜率乘积等于定值， 直线过定点。

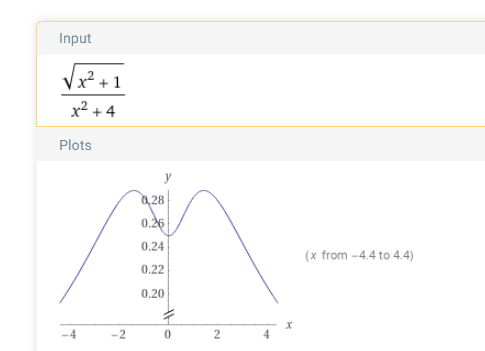
 10.一个函数图像

 

 求极值就是求导

 

 

 

 最大值等于1/6

无论是另m=1/k  ，把m转化为k ，还是只用m做运算，极大值 都不变， 图像有改变

 11.抛物线的性质

 

 

 

 

 

12

过点（a，0）  x=my+a    （1）

过点（0，b） 设 y=kx+b     （2）

（1）比（2）好，因为考虑到斜率不存在的情况。

 13.掌握常规问题是必修， 巧妙的方法是选修。但是鼓励研究。

 14.能画图就画图。

15.斜率的定义 

 

 

 

 

 

 

 x0=0，x1=1+1/b

 16.认识函数图像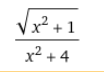

 

 

 

 

 

 

 

 17.有中点 做差

 18.有直角，列斜率乘积的方程。

19.尽量避开平方，

 

20. 过焦点 ，用焦点半径公式。

公式运用的越高级，计算就越简单，证明用的越初等，证明就越清晰。

 21 方程思想+ 定义域

 

 

 

 

 

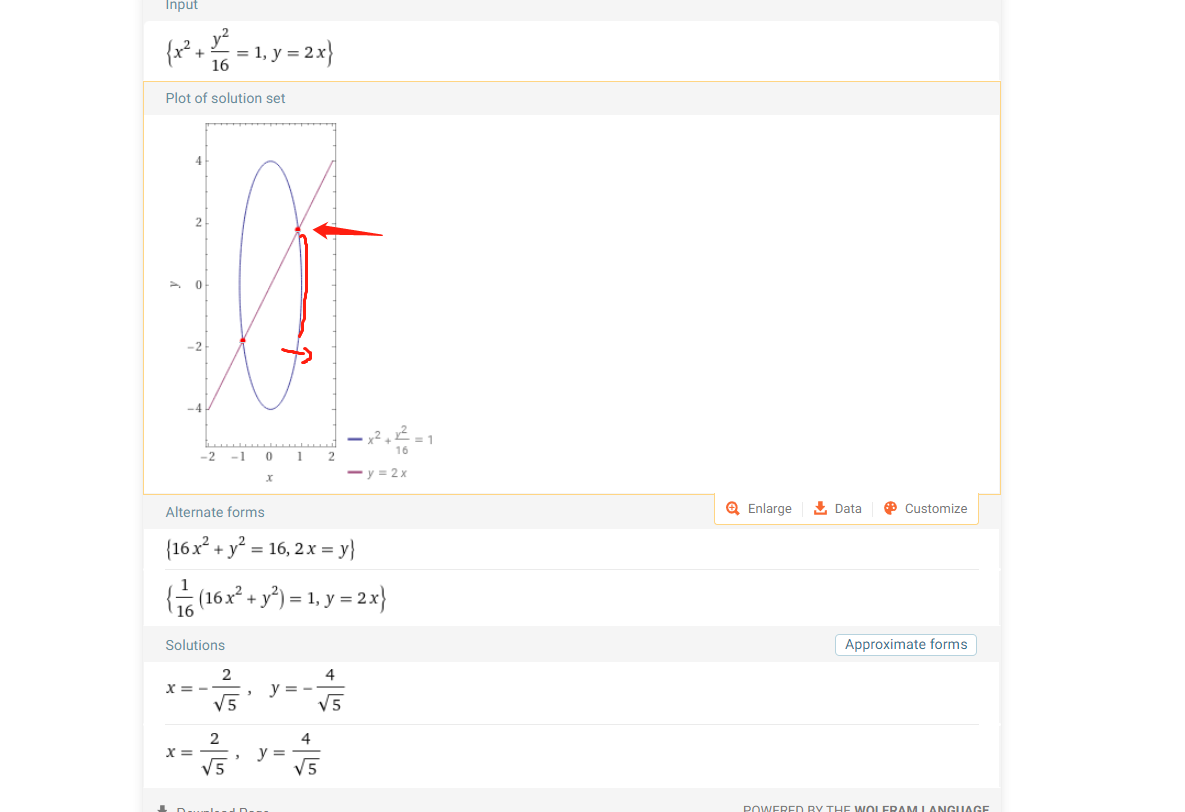
 红色区间才成立。所以x定义域有范围。

 22.分析大题，缺少思路。多写步骤，做出第一问，第二问 可以 直接放弃！

简单的题目必做对

中等层次的题目，按照检索关键词的方式，按照优先级套用公式。（重点）

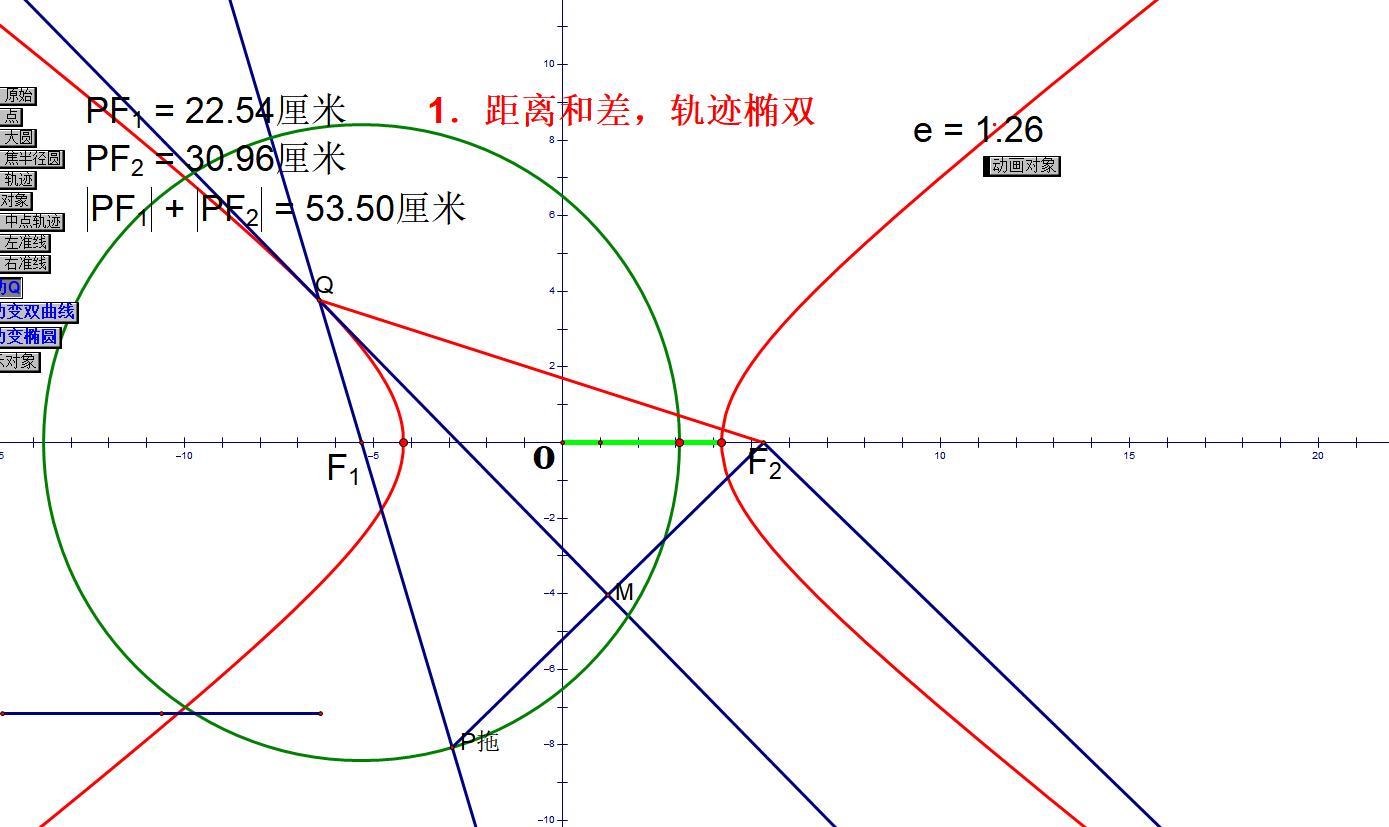
处理常见问题：动态轨迹

椭圆定义：

 

 

 

 

 

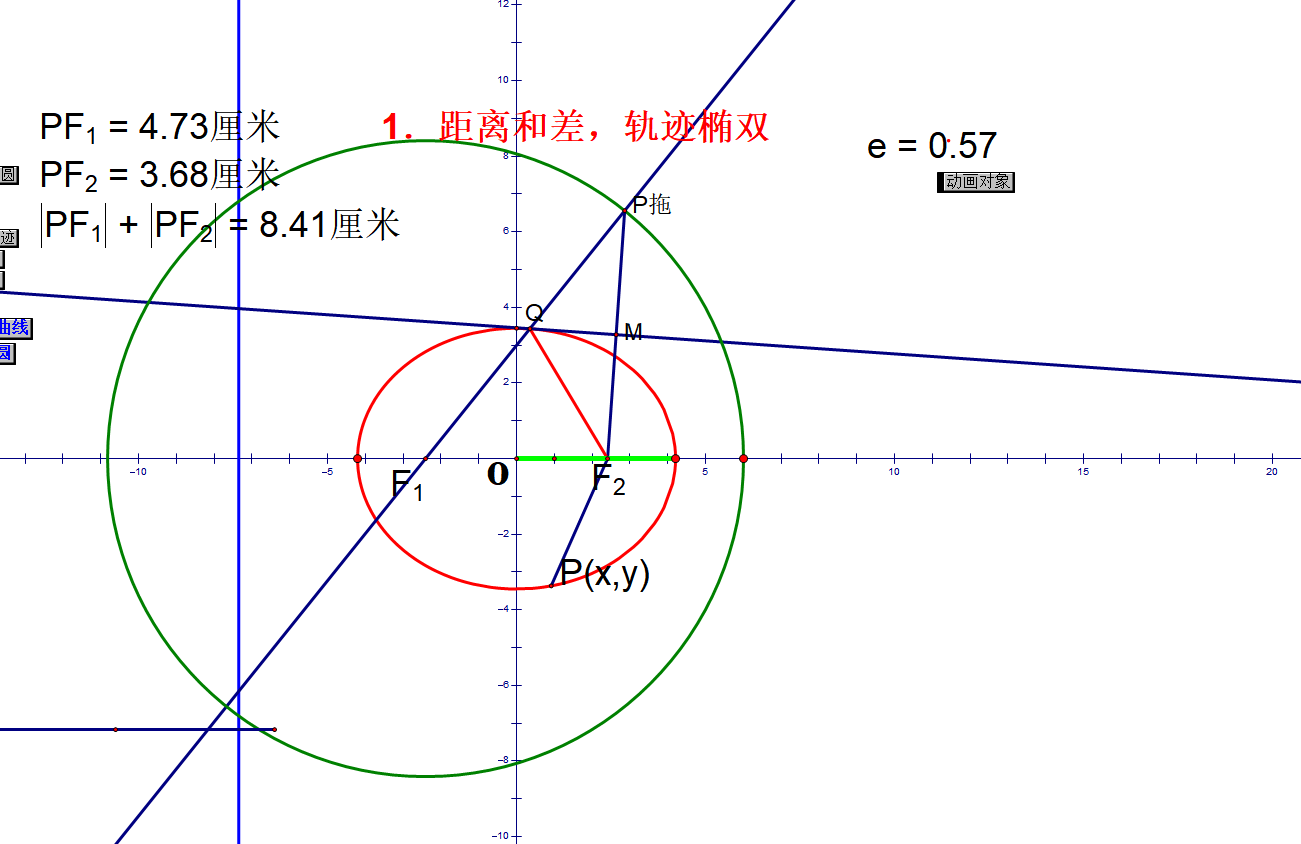
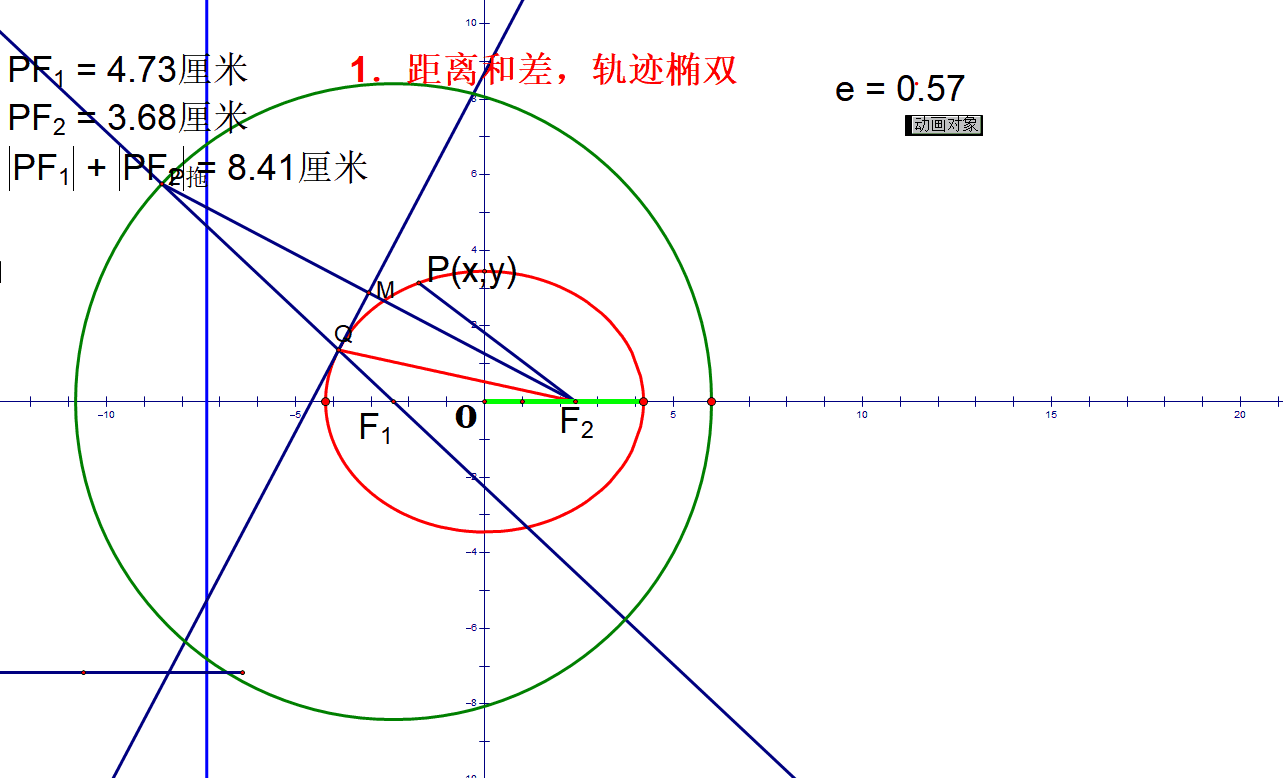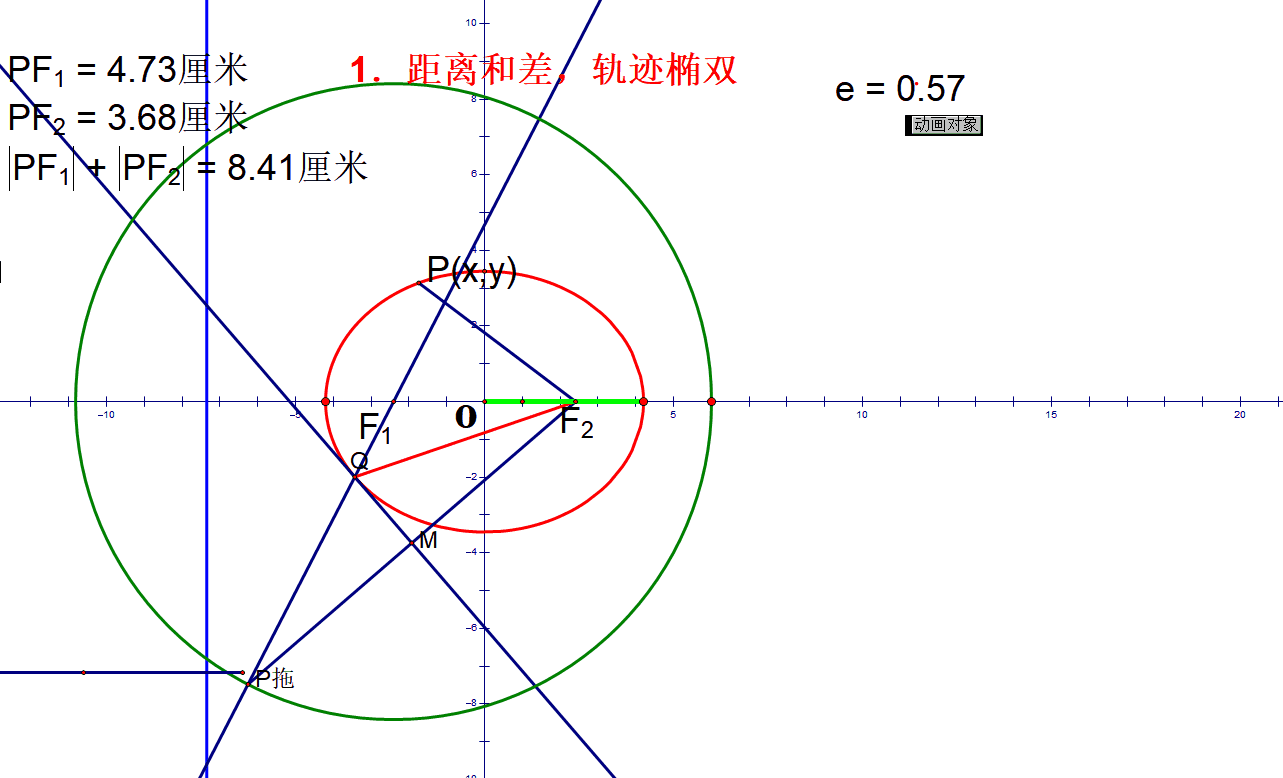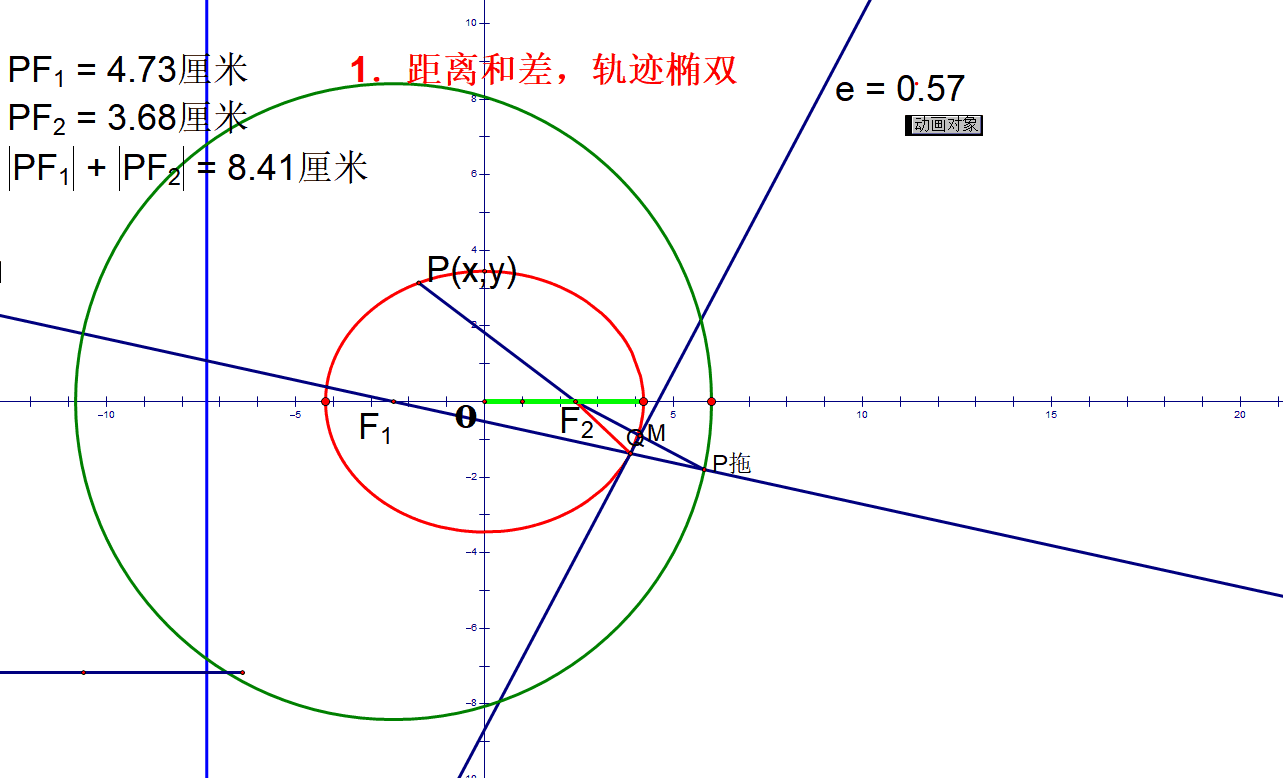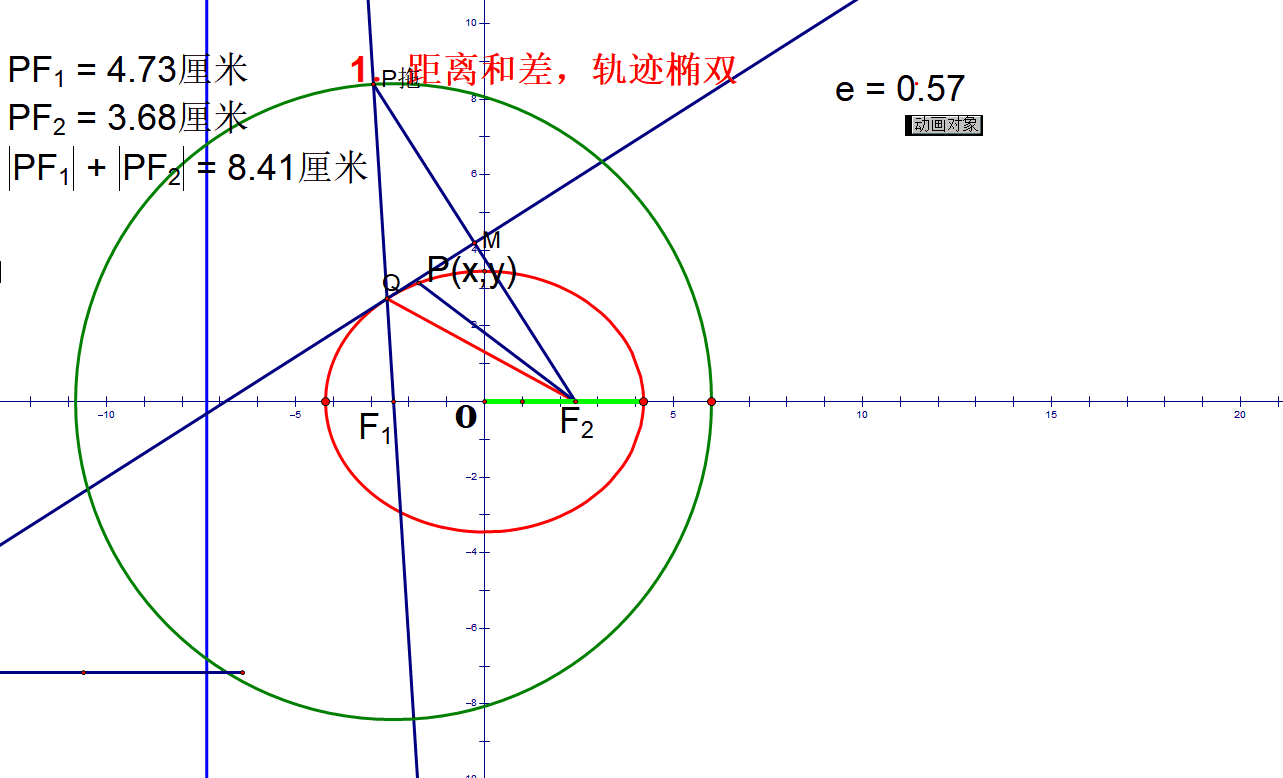
 双曲线定义