11/14
利用a b c ,得到 e f g。 已知什么能求什么?
时事 ,周围的案件,进入环境。
亲和力 激情 实力 理想气息 趣味性
融会贯通 多角度思考 系统性 直观性
传授一些 易错点,学生 不容易想到的地方,更进一步
一些技巧化简过程,节省计算时间
总分总 授课模式
总结 一张图谱网络所有
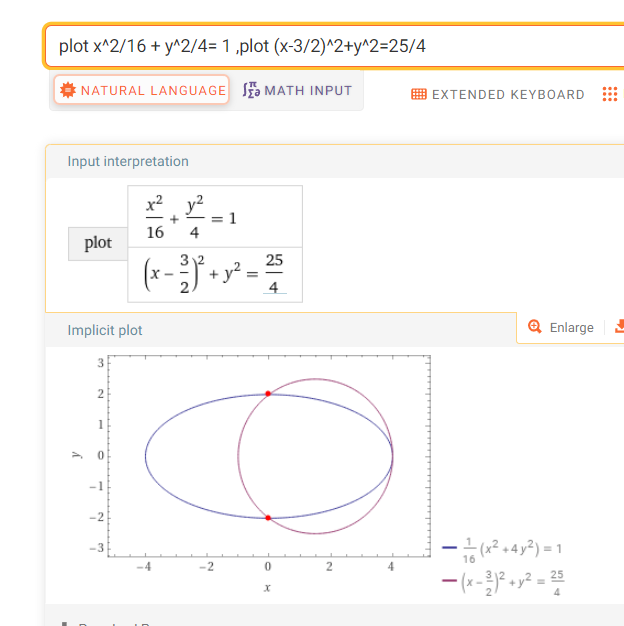
几何性质 代数性质
一本资料 ,系统的概括了所有性质。所有的你犯过的错题,你自己也要完善。那就是你的笔记。
借助工具:wolfram alpha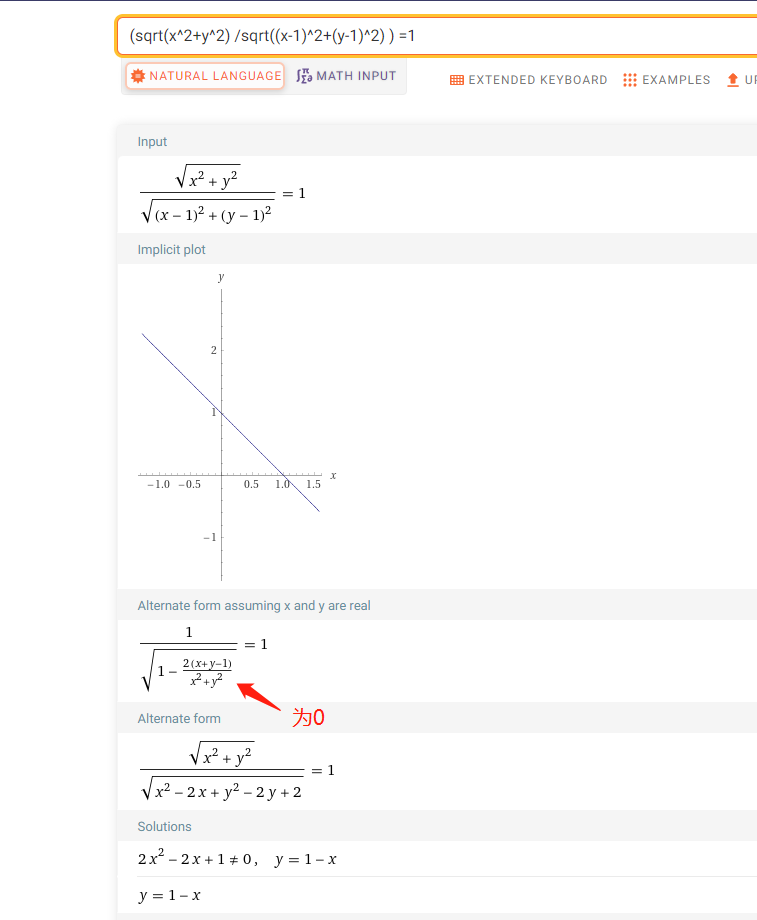
圆的定义: 动点到两个顶点比值不为1,就是圆。 为1就是 直线。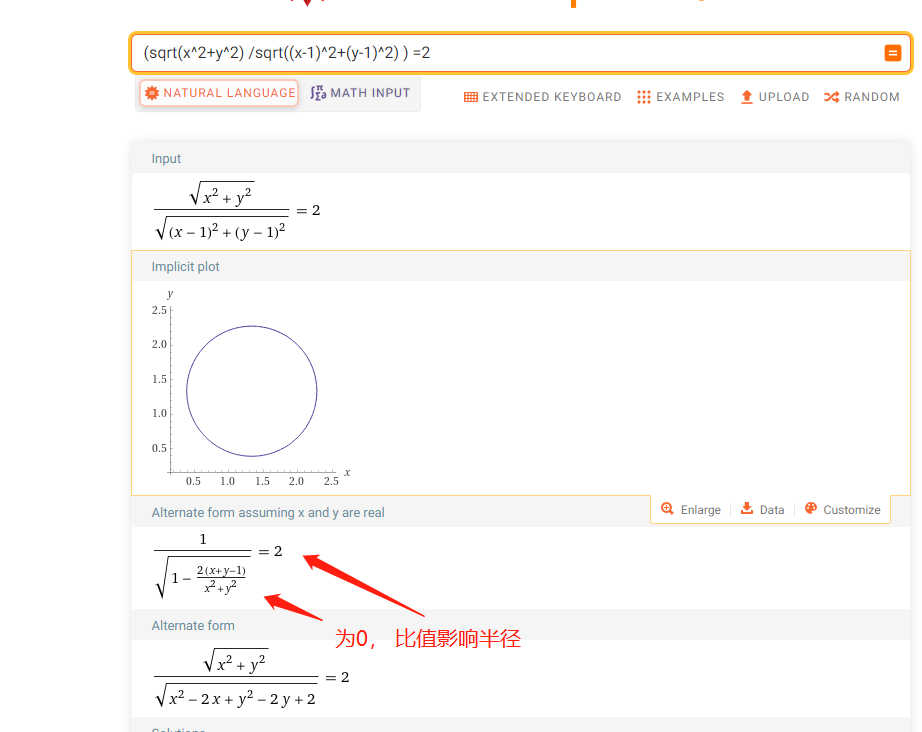
圆锥曲线 a b c e ,准线 ,知2求3
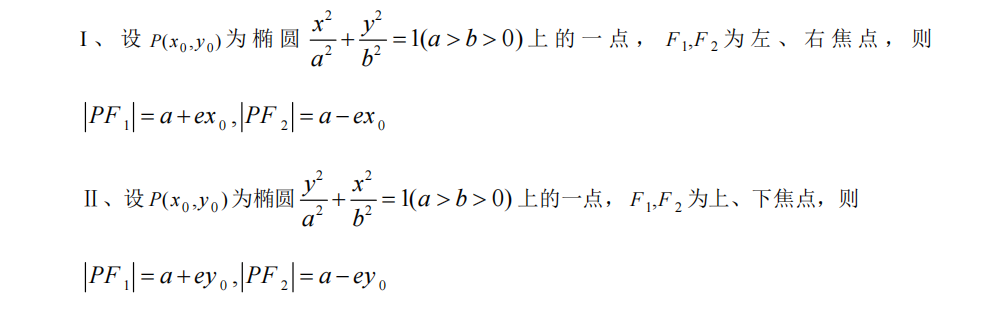


利用x的范围确认范围

双曲线的长轴在,把右边转化为1,的情况下,正号的未知数上。长轴只于符号有关,和系数无关。
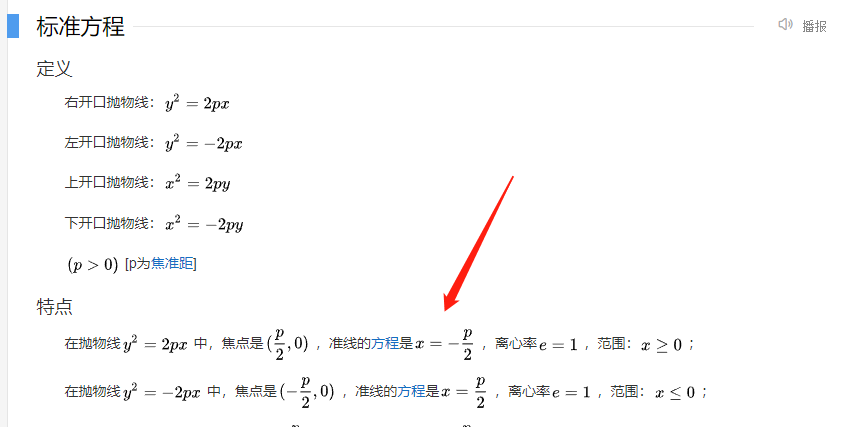
抛物线:准线是-p/2
双曲线:离心率相同,曲线可能不一样,焦点不一样,但是渐近线相同。
双曲线F点到渐近线的距离为b
抛物线曲线上面一点到焦点的距离等于x+p/2

简单的题目做法较多
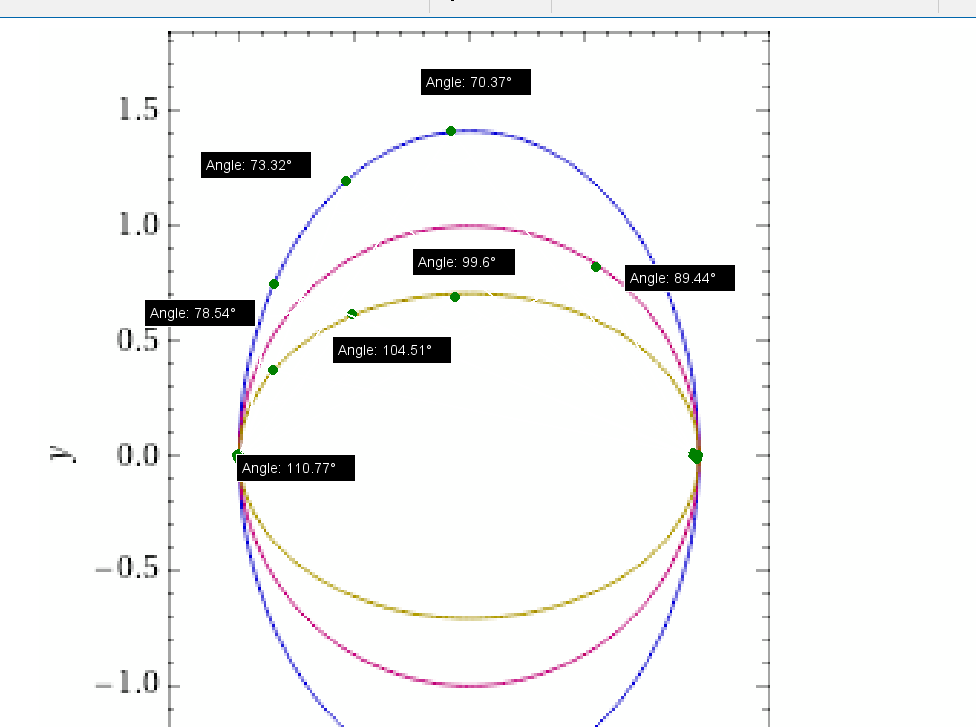
椭圆上面的点 如果比圆 高,角度越来越小,如果比圆低,角度越来越大。
测量角度的IC_Measure_2.0.0.286
链接:https://pan.baidu.com/s/1Emwn0OkN9aj4_ielZ-_Pog
提取码:1111
--来自百度网盘超级会员V4的分享
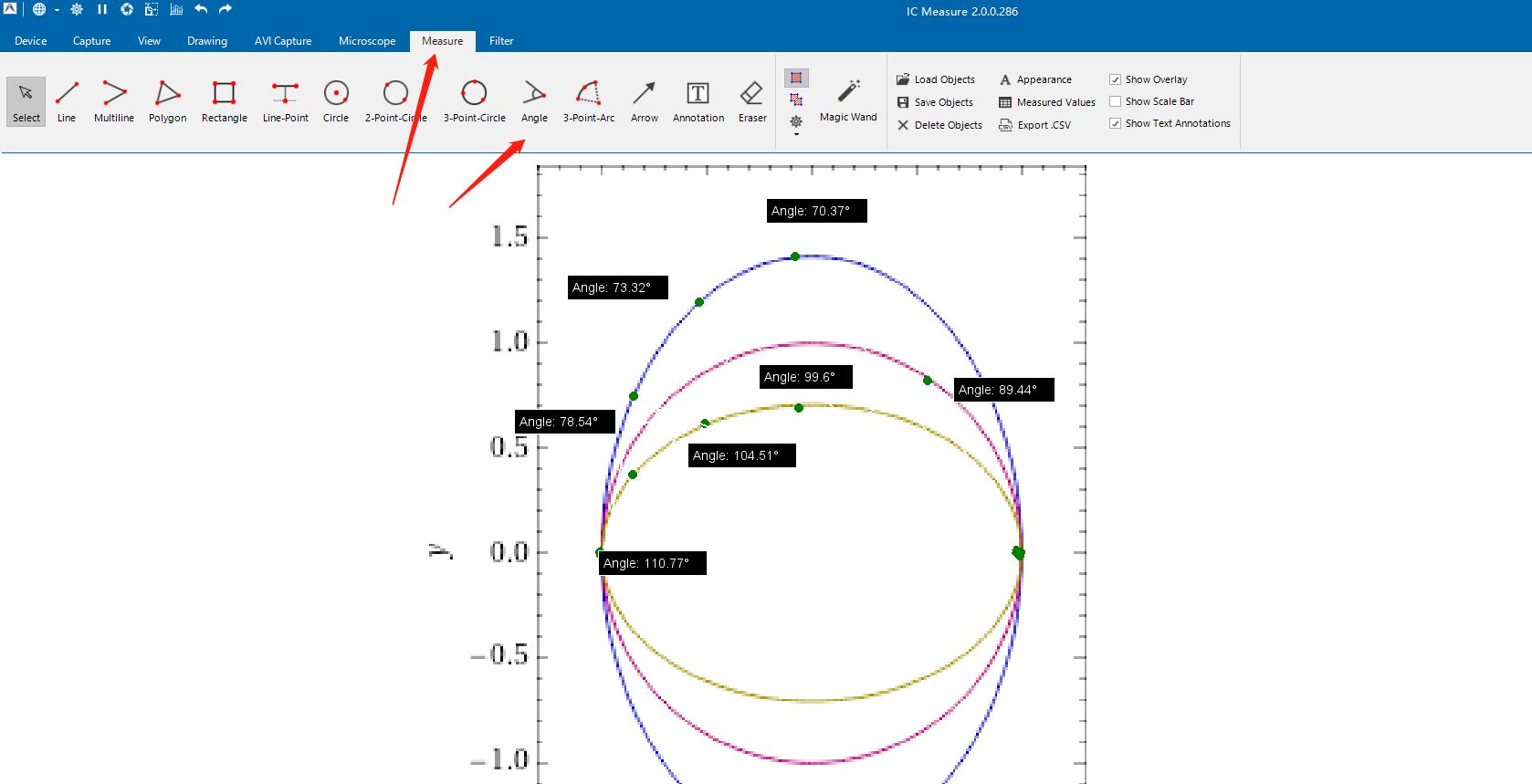
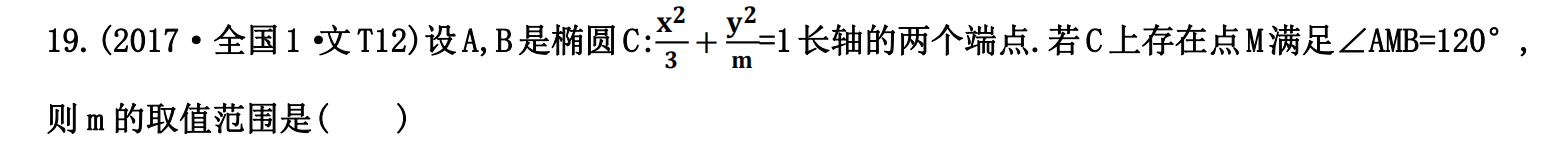

双曲线:系数乘积小于0即可

比值类,点不在圆锥曲线上,只能看直线,此题虽然是圆锥曲线,但是椭圆的作用只是提供了坐标。
题目中有向量,设点。

不等式结合 双曲线, ,画图,斜率从不同的角度来看,一个变陡峭一个变平缓。
此题既要设点又要设斜率k

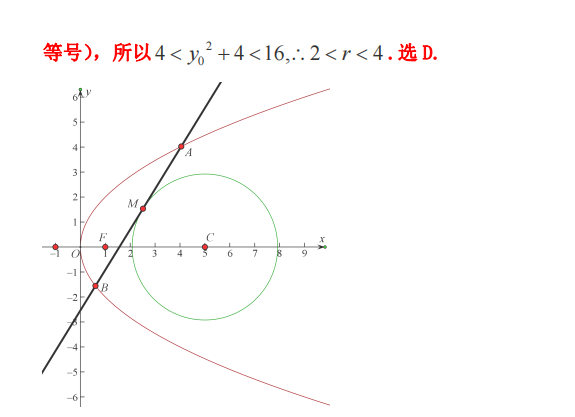
如果把抛物线性质改成是椭圆,圆心在原点,那么可以推出这个圆是标准圆。
如果圆心不在原点,在其他地方,同样可以利用向量垂直等于0,推导出斜率k 和交点中点M (X0,Y0)的关系,X0+kY0=a,a是圆心有关的常数。、
圆锥曲线,如果看见 有相切,就要设点 列出 向量垂直的方程。
实际上x轴上, 椭圆也有一条固定的x。
本题最厉害的地方,把动态的圆切点,归类垂直于到抛物线的一根垂线上面。使得y值的范围被确定。再带入圆的方程求出r的范围。
椭圆中原点同直线与椭圆交点构成三角形的面积的最大值



注意到:事实上,由于t一定可以取遍 ()(0,1) 之间的全体实数,所以方程内的所有参数对最终的结论都不产生影响。
因此,M点的位置对最终结论也不产生任何影响。
进而可知,M点如果不在x轴上,同样也是在 t=12 时取到最值。
所以,这个结论具有普遍性。
能画图就要画图
能用特殊的性质就不要用一般的性质。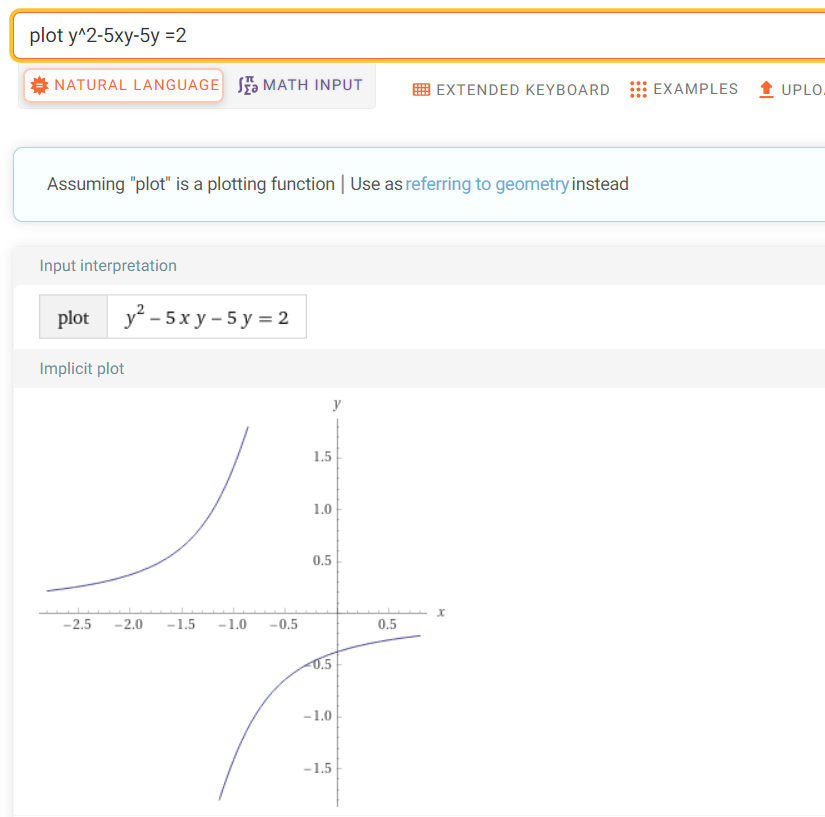
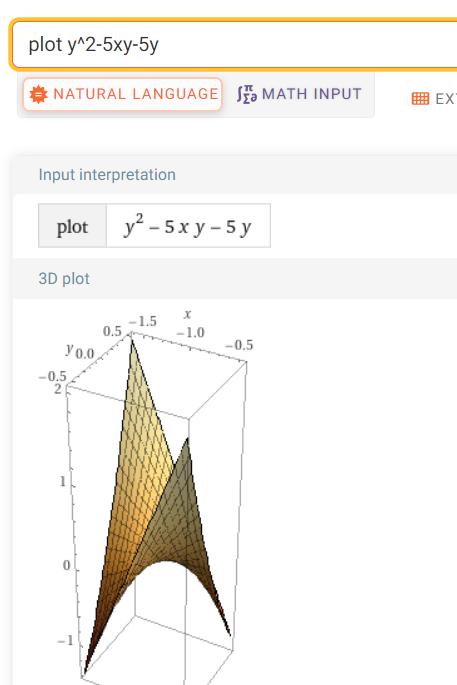
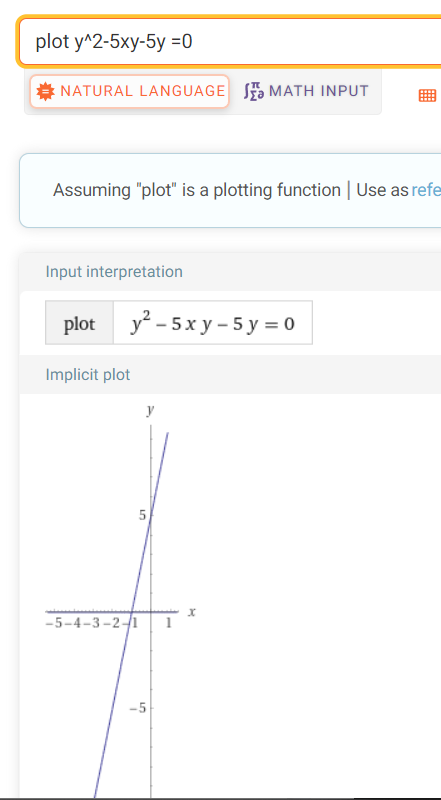
plot y^2-0.1xy-0.1y 是双曲面,等于什么值 就是截什么面,
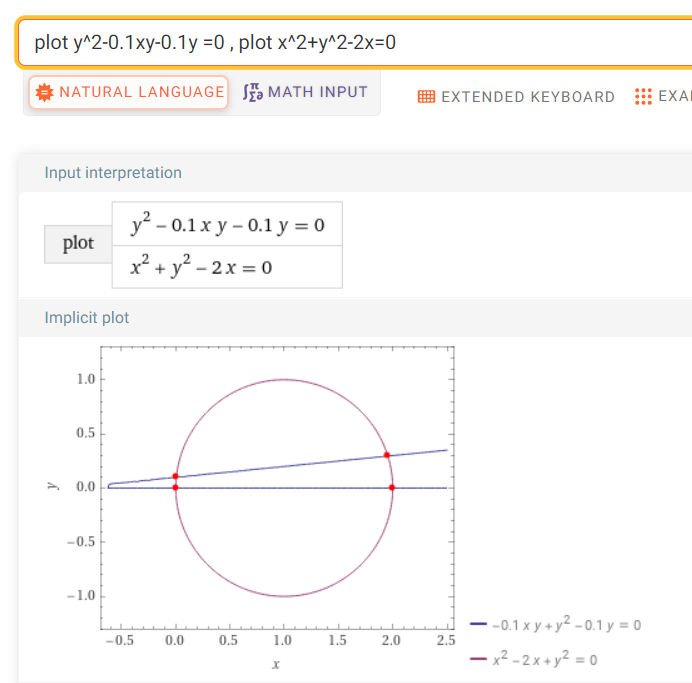
抛物线 三点为任意三角形,可以构造抛物线。