梯度下降法-理解共轭梯度法

 

 

 

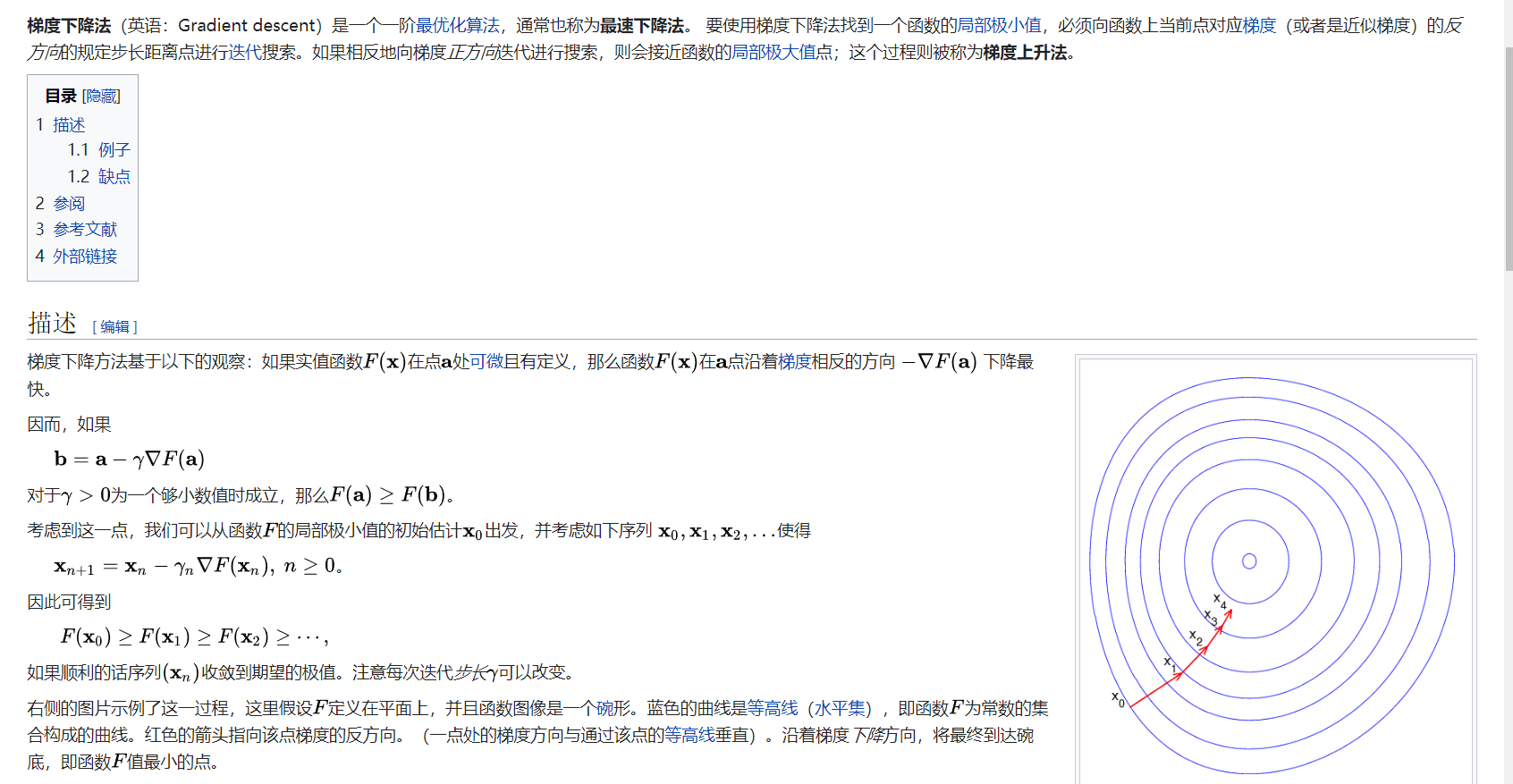
共轭梯度法关键是要找正交向量寻找方向，去不断逼近解。

其本质是最小二乘解的思想

最小二乘解

 

其中A系数矩阵是确定的，Ax是永远都取不到向量 b的，取得到那就是不用最小二乘解

 我要求AX和b最小的距离，就是要求b在Ax上的投影，向量b-AX一定是要垂直于AX的

 对A要求要满秩

 我的最小二乘法在于找到X，一开始我不理解迭代，因为很明显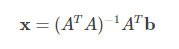这一步就能得到结果，共轭梯度法就是要逼近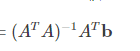

 

 

 

 共轭梯度法

1.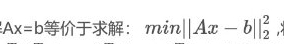换一种求解方式

 

 

2.

 

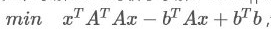 等于，而且A满秩，所以二次项里面的那个矩阵正定。

把   目标函数展开，化简，对每一项求ai 偏导，求出X的系数（在此假设已经找到了一组基能够表示X）

 

 

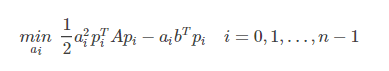对ai求偏导算出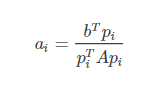

 

 这里解释为什么A正定

 

 

 

 

 3.寻找X使得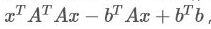最小

4.首先要在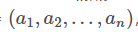张成的子空间上找到一组基来表示   x

5.事实上，已经有了一组基能表示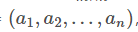空间

 

 

因为，x0等于0，所以r0等于b

 

 

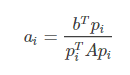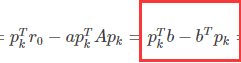因为，所以  才相等

 

 

 

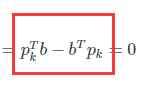 向量 pk  与向量b 同维，乘在一起数是相同的，相减就是0

 

 

因为来表示解很不方便，所以需要构造另外一组基来表示x

 

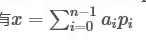 成立

 

由一组正交基导出正交基，自然想到了斯密特正交化

 

 

 比较难以理解的地方是

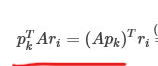因为A是正定矩阵，所以A 的转置等于A自己  但是Pk的转置等于pk t

 

 

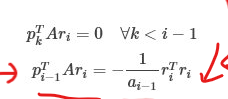 这里消除了 i 前面，所有项

是因为

再加上

 

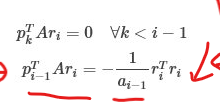
后面的基本上都看得懂