fisher线性判别

 

fisher 判决方式是监督学习，在新样本加入之前，已经有了原样本。

原样本是训练集，训练的目的是要分类，也就是要找到分类线。一刀砍成两半！

 

当样本集确定的时候，分类的关键就在于如何砍下这一刀！

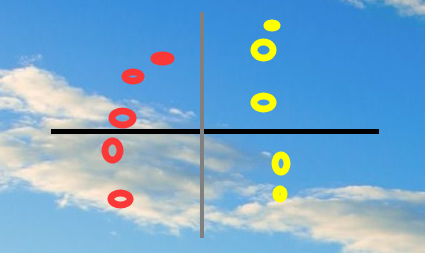
若以黑色的来划分，很明显不合理，以灰色的来划分，才是看上去合理的

 

1.先确定砍的方向

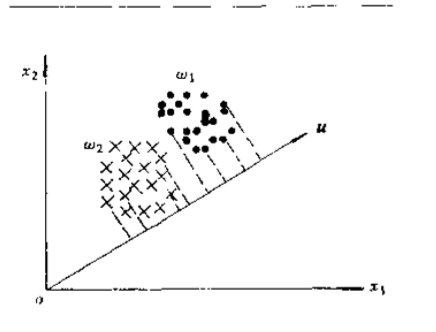
关键在于如何找到投影的向量u，与u的长度无关。只看方向

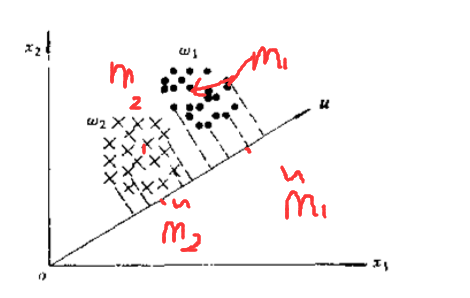
找到样本点的中心均值m1，m2，以及在向量u上的投影的m1~，m2~。

 

因为u的方向与样本点都有关，所以需要考虑一个含有所有样本点的表达式

不妨算出离差阵

算出类内离差矩阵，两个都要求出来，并求和

  

 

 

 并且投影的离差阵

 

 根据聚类的理想情况，类内距离小，类间距离大，所以就用类间去处理类内，我们现在的变量是向量u，我们就对u求导，算出max存在的时后u的条件。

 

为了方便化简，引入一个参数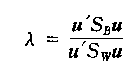 不要以为下面除以是向量，（1*2）*（2*2）（2*1）=1  维度变成1，这是一个常数。

 

当求导公式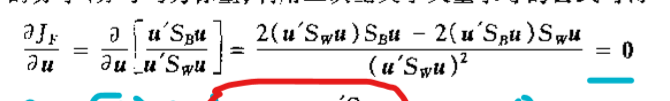

分子为0的时候，推出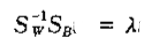

所以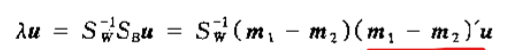

而且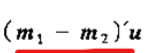是（1*2）*（2*1）等于1，也是一个常数

 

到此为止，u的方向已经确定了

2.具体切哪一个点。

a，切

 

 切投影均值的终点

2.

切贝叶斯概率的比例点

方向和具体点均已找到，分析完毕