p68理想的性质

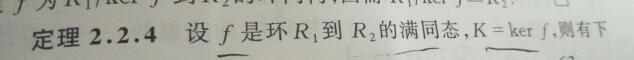
1.如何由2.2.4推出后面的结论?
2.为什么A可以等于R？
3.如何证明3？

 

1.  π：R->R/M套用定理2.2.4（2）和（1）

R2是R/M，I是R/M的理想也就是R2的理想，所以f^(-1)I  就能在R1找到一个理想，设为A。使得 I=π（a）  I=A/M。M是极大理想，

2.没有真包含极大理想的真理想（不是R的理想），所以A只能是R或M，因为I=A/M,所以I等于或者R/M,  R本身是自己的理想。

3.由2.2.4（2）推出2.3.5中的R的理想A对应的π（A）=A/M是R/M,的理想，

域的理想就是0和他自己，所以A/M等于0或者R/M