数论函数综合

一.数论函数

1.定义

数论函数是 : 其定义域是正整数，值域是一个数集的函数。

积性函数 : 对于所有互质整数 $a$ 和 $b$ 有性质$f(ab)=f(a)f(b)$的数论函数。

完全积性函数 : 对于所有整数 $a$ 和 $b$ 有性质$f(ab)=f(a)f(b)$的数论函数。

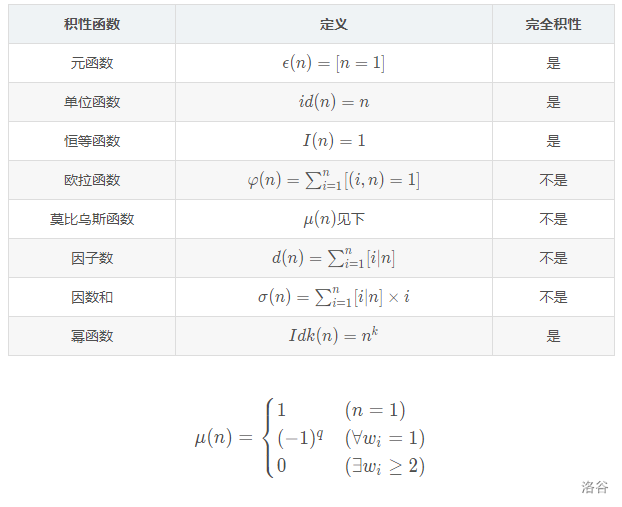
常见的的积性函数：

2.性质

1.对于任意正整数 $n$ , $\sum_{i|n}\varphi(i)=n$

不妨令 $f(n)=\sum_{i|n}\varphi(i)$ ， 首先证明 $f$ 是一个积性函数。

因为 $n , m$ 互质

$$\begin{aligned} f(n) \times f(m) &=\sum_{i|n}\varphi(i) \times \sum_{j|m}\varphi(j) \\ &=\sum_{ij|nm}\varphi(i) \times \varphi(j) \\ &=\sum_{ij|nm}\varphi(ij) \\ &=f(n \times m) \\ \end{aligned}$$

因为 $n=p_1^{w_1} \times p_2^{w_2} \times ... \times p_k^{w_k}$ , 且 $f$ 为积性函数 ， 所以只需求出 $f(p_i^{w_i})$ 即可。

$$\begin{aligned} f(p_i^{w_i})&=\sum_{d|p_i^{w_i}}\varphi(d) \\ &=\varphi(1)+\varphi(p_i)+\varphi({p_i}^2)+...+\varphi({p_i}^{w_i}) \\ &=1+(p_i-1)+({p_i}^2-p_i)+...+({p_i}^{w_i}-{p_i}^{w_i-1}) \\ &={p_i}^{w_i} \end{aligned}$$

所以 $f(n)=n$ , 即 $\sum_{i|n}\varphi(i)=n$。

2.对于任意正整数 $n$ , $\sum_{i|n}\mu(i)=[n=1]$

证明如下：

1.当 $n=1$ 时显然

2.当 $n!=1$ 时，由唯一分解定理得：$n=p_1^{w_1}p_2^{w_2}...p_k^{w_k}$
由莫比乌斯函数的性质，$\mu(k) \not= 0$ 当且仅当 $k$ 无平方因子。(由多个质因子相乘)

有 $i$ 个质因子的数有 $C_k^i$ 种取值。

所以只需证

$$\sum_{i=0}^k(-1)^iC_k^i=0$$

很像二项式定理，将 $x = 1 , y = -1$ 代入即可得证。

3.对于任意正整数 $n$ ，$\sum_{d|n}\frac{\mu(d)}{d}=\frac{\varphi(n)}{n}$

这个一会儿再证。

二.狄利克雷卷积

两个数论函数 $f$ 和 $g$ 的卷积为 $t(n)=( f \times g )(n)=\sum_{d|n}f(d) \times g(\frac{n}{d})$。

前面的括号代表将 $f$ 卷 $g$ ，后面的括号代表范围。

简记为$t=f*g$。

狄利克雷卷积满足交换律，结合律与分配律。

若 $f$ 是任意积性函数 ， 则 $f*\epsilon=f$

---

较为常见数论函数的迪利克雷卷积：

$$d = I * I$$

$$σ = id * I$$

$$id=\varphi * I$$

$$\epsilon = \mu * I$$

$$φ = μ* id$$

其中，后三项分别对应积性函数的三个性质。

现在证一下 $φ = μ* id$

$$\begin{aligned} &\varphi * I=id \\ \Rightarrow&\varphi*I*\mu=id*\mu \\ \Rightarrow&\varphi=id*\mu \\ &\end{aligned}$$

即

$$\varphi(n)=\sum_{d|n}\frac{n}{d}*\mu(d)$$

两边同时除以 $n$ , 得

$$\frac{\varphi(n)}{n}=\sum_{d|n}\frac{\mu(d)}{d}$$

就是上文提到的性质$3$。

三.数论分块

1.引入

题目给你这样一个式子：

$$\sum_{i=1}^{n}\lfloor\frac{n}{i} \rfloor$$

这不是暴力吗？

那如果$n \le 10^{12}$ 呢？再见

这时我们就要用到一个神奇的结论——数论分块

2.思想

再看一眼式子，我们发现，很多值是一样的。

如果我们知道分布规律，那么这一段就可以一起求解了。

结论是：若一段区间的左端点为$l$，那么区间值为 $\lfloor \frac{n}{l} \rfloor$ ,区间右端点 $r=\lfloor \frac{n}{\lfloor \frac{n}{l} \rfloor} \rfloor$

证明如下：

设 $k=\lfloor \frac{n}{l} \rfloor , p=n~mod~l$ , 则$n=k*l+p$

若 $\lfloor \frac{n}{l+d} \rfloor = k$ , 则 $n = k*(l+d)+p'$

两个式子相减得：$p'=p-kd$ , 又因为 $0 \le p,p' \le l-1$

所以 $d$ 的最大值为 $\lfloor \frac{p}{k} \rfloor$。

那么，

$$\begin{aligned} r&=l+d \\ &=l+\lfloor \frac{p}{k} \rfloor \\ &=l+\lfloor \frac{n~mod~l}{ \lfloor \frac{n}{l} \rfloor } \rfloor \\ &=l+\lfloor \frac{n- \lfloor \frac{n}{l} \rfloor * l}{ \lfloor \frac{n}{l} \rfloor } \rfloor \\ &=\lfloor l+ \frac{n- \lfloor \frac{n}{l} \rfloor * l}{ \lfloor \frac{n}{l} \rfloor } \rfloor \\ &=\lfloor \frac{\lfloor \frac{n}{l} \rfloor * l}{\lfloor \frac{n}{l} \rfloor} + \frac{n- \lfloor \frac{n}{l} \rfloor *l}{ \lfloor \frac{n}{l} \rfloor } \rfloor \\ &=\lfloor \frac{n}{\lfloor \frac{n}{l} \rfloor}\rfloor \end{aligned}$$

3.代码实现

for( int l = 1 , r ; l <= n ; l = r + 1 ) {
	r = n / (n / l);
	\\具体内容例题会讲到
}

数论分块大多数情况是和数论函数一起使用

4.例题

1.P2261 [CQOI2007]余数求和

题目要求的是

$$\sum_{i=1}^nk~mod~i$$

$$\Rightarrow \sum_{i=1}^n k-\lfloor \frac{k}{i} \rfloor * i$$

$$\Rightarrow n*k-\sum_{i=1}^n \lfloor \frac{k}{i} \rfloor * i$$

然后 ，因为在 $l-r$ 区间内 $\lfloor \frac{k}{i} \rfloor$ 的值相等，$i$ 递增，所以这段区间内是一个等差数列 ( 首项为 $l*\lfloor \frac{k}{i} \rfloor$ , 末项为 $r * \lfloor \frac{k}{i} \rfloor$ , 公差为 $\lfloor \frac{k}{i} \rfloor$ ) ， 对于每一段区间计算和即可。

注意，$Ans$ 计算的是 $\sum_{i=1}^n \lfloor \frac{k}{i} \rfloor * i$ 。

#include <cstdio>
#include <iostream>
using namespace std;

int n , k;
long long Ans;

int main( ) {
	scanf("%d %d",&n,&k);
	for( int l = 1 , r ; l <= n ; l = r + 1 ) {
		r = k / l == 0 ? n : min( n , k / ( k / l ) );
		Ans += 1ll * ( k / l ) * ( l + r ) * ( r - l + 1 ) / 2; 
	}
	printf("%lld", 1ll * n * k - Ans );
	return 0;
} 

2.P3935 Calculating

3.P2260 [清华集训2012]模积和 & P2834 能力测验

四.莫比乌斯函数与莫比乌斯反演

1.莫比乌斯函数

由唯一分解定理得：

$$n=p_1^{w_1}p_2^{w_2}...p_q^{w_q}$$

$$\mu(n)=\begin{cases}1 & (n=1)\\ (-1)^q & (\forall w_i=1) \\ 0 & (\exists w_i \ge 2) \end{cases}$$

通俗来讲，$\mu(1)=1$ ，当 $n$ 存在平方因子时 $\mu(n)=0$

否则 $\mu(n)=(-1)^k$ ， $k$ 为质因子数。

附一份线性筛的代码:

void sieve( int x ) {
	mu[ 1 ] = 1;
	for( int i = 2 ; i <= x ; i ++ ) {
		if( !vis[ i ] ) {
			prime[ ++ k ] = i;
			mu[ i ] = -1;
		}
		for( int j = 1 ; j <= k && 1ll * i * prime[ j ] <= x ; j ++ ) {
			vis[ i * prime[ j ] ] = 1;
			if( i % prime[ j ] == 0 ) break;
			mu[ i * prime[ j ] ] = -mu[ i ];
		}
	}
}

2.莫比乌斯反演

1.形式1

如果

$$F(n)=∑_{d|n}f(d)$$

则有

$$f(n)=∑_{d|n}μ(d)F(\frac{n}{d})$$

证法1.狄利克雷卷积

$$F=f*I$$

$$F*\mu=f*I*\mu$$

$$F*\mu=f*\epsilon$$

$$f=F*\mu$$

证法2.和式变化

$$\begin{aligned} &∑_{d|n}μ(d)F(\frac{n}{d})\\ =&∑_{d|n}μ(d)\sum_{s|\frac{n}{d}}f(s)\\ =&∑_{d|n}f(d)\sum_{s|\frac{n}{d}}\mu(s)\\ =&∑_{d|n}f(d)[\frac{n}{d}=1] \\ =& f(n) \end{aligned}$$

2.形式2

如果

$$F(n)=∑_{n|d}f(d)$$

则有

$$f(n)=∑_{n|d}μ(d)F(\frac{d}{n})$$

1.证法1.和式变化

$$\begin{aligned} &∑_{n|d}μ(d)F(\frac{d}{n}) \\ =&∑_{n|d}μ(d)\sum_{\frac{d}{n}|s}f(s)\\ =&∑_{n|d}f(d)\sum_{\frac{d}{n}|s}\mu(s)\\ =&∑_{n|d}f(d)[\frac{d}{n}=1] \\ =& f(n) \end{aligned}$$

2.证法2.莫比乌斯函数

$$\begin{aligned} &∑_{n|d}μ(d)F(\frac{d}{n})\\ =&∑_{n|d}\mu(\frac{d}{n})F(d)\\ =&∑_{n|d}\mu(\frac{d}{n})\sum_{d|s}f(s)\\ \end{aligned}$$

因为 $d$ , $s$ 分别为 $n$ , $d$ 倍数， 所以设 $d=n \times k , s=d \times t$,上式即为

$$∑_{k=1}μ(k)\sum_{t=1}f( (k \times t) \times n)$$

观察发现,对于每一个 $k$ ，它会将所有的倍数贡献 $\mu(k)$ 个。

反过来将，对于一个$f(an)$，它出现的次数为$\sum_{d|a}\mu(d)=[a=1]$。

所以只有当 $a=1$ 时，$f(1*n)=f(n)$ 会刚好出现一次。

所以上式等于 $f(n)$。

3.例题

1.Luogu P3455 求 $\sum_{i=1}^n\sum_{j=1}^m[gcd(i,j)=d]$( $d$已知 )

题解

2.Luogu P1829 求 $\sum_{i=1}^n\sum_{j=1}^mlcm(i,j)$

题解

3.cqbzoj P6388 求 $\sum_{i=1}^n\sum_{j=1}^mgcd(i,j)$

题解

4.Luogu P3704 求 $\sum_{i=1}^n\sum_{j=1}^mf_{gcd(i,j)}$ , $f$为斐波拉契数列。

题解

五.杜教筛

一.前言

一般来说，反演的题目都需要积性函数的前缀和，一般都能用线性筛解决。

但是，如果良心出题人将 $n$ 出到 $10^9$ ， 我们就需要使用一种非线性时间筛法。

二.推导

首先设要计算的函数为 $f$ ， $S$ 为其前缀和。

构造出两个函数 $g$ , $h$ , 使得 $h=f * g$ , 即 $h(n)=\sum_{d|n}f(d)*g(\frac{n}{d})$

显然有：

$$\begin{aligned} \sum_{i=1}^{n}h(i)&=\sum_{i=1}^n\sum_{d|i}g(\frac{i}{d})* f(d) \\ &=\sum_{i=1}^n\sum_{db=i}g(d) * f(b)\\ &=\sum_{d=1}^ng(d)\sum_{b=1}^{\lfloor \frac{n}{d} \rfloor}f(b)\\ &=\sum_{d=1}^ng(d)S(\lfloor \frac{n}{d} \rfloor)\\ &=g(1)S(n)+\sum_{d=2}^ng(d)S(\lfloor \frac{n}{d} \rfloor)\\ \end{aligned}$$

$$\Rightarrow g(1)S(n)=\sum_{i=1}^{n}h(i)-\sum_{d=2}^ng(d)S(\lfloor \frac{n}{d} \rfloor)$$

这就是杜教筛的一般形式了。

3.应用

一般来讲，在杜教筛时，$h$ 的前缀和可以快速求得 ， $g$ 的前缀和也尽量简单。

大部分是狄利克雷卷积的形式。

1.求 $S(n)=\sum_{i=1}^n\mu(i)$

容易想到 ， $\mu*I=\epsilon$ ， 即 $g$ 为 $I$ , $h$ 为 $\epsilon$。

代入上式得：

$$S(n)=1-\sum_{d=2}^nS(\lfloor \frac{n}{d} \rfloor)$$

附一份代码：

int Summu( int n ) {
	if( n <= MAXN ) return summ[ n ]; //预处理
	if( Mapm[ n ] ) return Mapm[ n ]; //记忆化
	
	int Ans = 1;
	for( int l = 2 , r ; l <= n ; l = r + 1 ) {
		r = n / ( n / l );
		Ans -= ( r - l + 1 ) * Summu( n / l ); 
	}
	return Mapm[ n ] = Ans;
}

2.求 $S(n)=\sum_{i=1}^n\varphi(i)$

容易想到 ， $\varphi*I=id$ ， 即 $g$ 为 $I$ , $h$ 为 $id$。

代入上式得：

$$S(n)=\frac{n*(n+1)}{2}-\sum_{d=2}^nS(\lfloor \frac{n}{d} \rfloor)$$

附一份代码：

int Sumphi( int n ) {
	if( n <= MAXN ) return sump[ n ]; //预处理
	if( Mapp[ n ] ) return Mapp[ n ]; //记忆化
	
	int Ans = n * ( n + 1 ) / 2;
	for( int l = 2 , r ; l <= n ; l = r + 1 ) {
		r = n / ( n / l );
		Ans -= ( r - l + 1 ) * Sumphi( n / l ); 
	}
	return Mapp[ n ] = Ans;
}

结合 $1,2$ 就是 P4213 【模板】杜教筛（Sum）。

3.求 $S(n)=\sum_{i=1}^n\varphi(i) \times i^2$

在迪利克雷卷积中，$id * id$ 会是一个非常好的式子，因为这样可以约分。

我们不妨构造函数 $g(n)=n^2$ , 来约掉$f(n)$所含的$n^2$。

$$\begin{aligned} h(n)&=\sum_{d|n}f(d) \times g(\frac{n}{d}) \\ &=\sum_{d|n}\varphi(d) \times d^2 \times (\frac{n}{d})^2\\ &=n^2\sum_{d|n}\varphi(d)\\ &=n^3 \end{aligned}$$

$h,g$前缀和非常容易得到

$\sum_{i=1}^nh(i)=\frac{n^2(n+1)^2}{4}$

$\sum_{i=1}^ng(i)=\frac{n(n+1)(2n+1)}{6}$

带入杜教筛的式子:

$$g(1)S(n)=\sum_{i=1}^{n}h(i)-\sum_{d=2}^ng(d)S(\lfloor \frac{n}{d} \rfloor)$$

$$S(n)=\frac{n^2(n+1)^2}{4}-\sum_{d=2}^ng(d)S(\lfloor \frac{n}{d} \rfloor)$$

然后就可以做 P3768 简单的数学题

参考题解

4.求 $S(n)=\sum_{i=1}^n d(i)$

首先有 $d=I*I$

容易想到 ， $\mu*d=I$ ， 即 $g$ 为 $\mu$ , $h$ 为 $I$。

代入上式得：

$$S(n)=n-\sum_{d=2}^n \mu(d)S(\lfloor \frac{n}{d} \rfloor)$$

然后可以用杜教筛同步筛出 $\mu$ 和 $d$ 的前缀和。

原题 P6788 「EZEC-3」四月樱花

参考资料

数论函数

莫比乌斯反演

杜教筛