快速傅里叶变换(fft)
一.复数
1.概念
复数就是形如 \(a+bi\) 的数，其中 \(a,b\) 是实数，且\(b≠0,i^2=- 1\)。
其中实数 \(a\) 和 \(bi\) 分别被称为复数的实部和虚部。
2.四则运算
1.加法 \((a+bi)+(c+di)=(a+c)+(b+d)i\)
2.减法 \((a+bi)-(c+di)=(a-c)+(b-d)i\)
3.乘法 \((a+bi) \times (c+di)=(ac-bd)+(ad+bc)i\)
4.除法 \((a+bi) \div (c+di)=\frac{(a+bi)(c-di)}{(c+di)(c-di)}=\frac{ac-bd}{c^2-d^2}+\frac{bc-ad}{c^2-d^2}i\)
struct Complex {
double x , y;
Complex operator + ( const Complex &a ) const {
return { x + a.x , y + a.y };
}
Complex operator - ( const Complex &a ) const {
return { x - a.x , y - a.y };
}
Complex operator * ( const Complex &a ) const {
return { x * a.x - y * a.y , x * a.y + y * a.x };
}
Complex operator / ( const Complex &a ) const {
return { ( x * a.x - y * a.y ) / ( a.x * a.x - a.y * a.y ) , ( y * a.x - x * a.y ) / ( a.x * a.x - a.y * a.y ) };
}
};
3.几何意义
每一个复数可以由直角坐标系上的点唯一确定，\(x\)轴称为实轴，\(y\)轴称为虚轴。
复数乘法有个重要的性质：模长相乘，幅角相加。
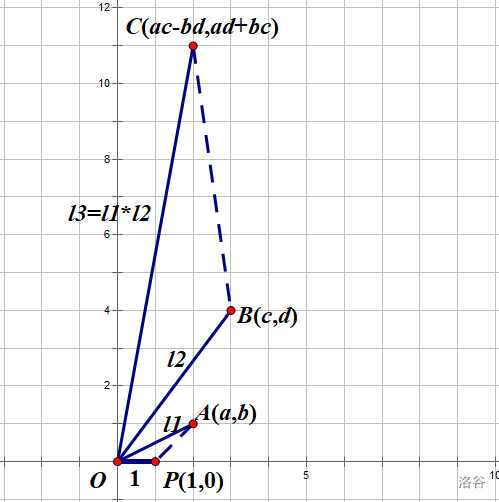
1.模长相乘
\[\begin{aligned}
l_1&=\sqrt{a^2+b^2} \\
l_2&=\sqrt{c^2+d^2} \\
l_3&=\sqrt{(ac-bd)^2+(ad+bc)^2} \\
&=\sqrt{(ac)^2+(bd)^2-2abcd+(ad)^2+(bc)^2+2abcd} \\
&=\sqrt{(ac)^2+(bd)^2+(ad)^2+(bc)^2} \\
&=\sqrt{a^2(c^2+d^2)+b^2(c^2+d^2)} \\
&=\sqrt{(a^2+b^2)(c^2+d^2)} \\
&=\sqrt{(a^2+b^2)}\sqrt{(c^2+d^2)} \\
&=l_1l_2 \\
\end{aligned}\]
2.幅角相加
证明 \(\triangle AOP\) 与 \(\triangle COB\) 相似即可。
首先有：
\[\frac{AO}{CO}=\frac{OP}{OB}=\frac{1}{l_2}
\]
只需证：
\[\begin{aligned}
\frac{AP}{CB}&=\frac{1}{l_2} \\
\frac{AP}{CB}&=\frac{\sqrt{(a-1)^2+b^2}}{\sqrt{(ac-bd-c)^2+(ad+bc-d)^2}} \\
&=\frac{\sqrt{a^2+b^2-2a+1}}{\sqrt{((ac)^2+(bd)^2+c^2-2abcd-2ac^2+2bcd)+((ad)^2+(bc)^2+d^2+2abcd-2ad^2-2bcd)}} \\
&=\frac{\sqrt{a^2+b^2-2a+1}}{\sqrt{(ac)^2+(bd)^2+(ad)^2+(bc)^2+c^2+d^2-2ac^2-2ad^2}} \\
&=\frac{\sqrt{a^2+b^2-2a+1}}{\sqrt{(c^2+d^2)(a^2+b^2-2a+1)}} \\
&=\frac{1}{\sqrt{c^2+d^2}}=\frac{1}{l_2} \\
\end{aligned}\]
二.复数单位根
1.概念
\(n\) 次单位根是 \(n\) 次幂为 \(1\) 的复数。
\(1\)的模长为\(1\)，所以 \(n\) 次单位根的模长也为\(1\)，即在单位圆上。
因为模长均为\(1\)，所以在单位圆上，我们只需考虑幅角。
不难想到，幅角为 \(\frac{2\pi}{n}\alpha\) 的复数，都是单位根。
\(n\) 次单位根一共有 \(n\) 个，且等分单位圆。如图便是所有的 \(6\) 次单位根。
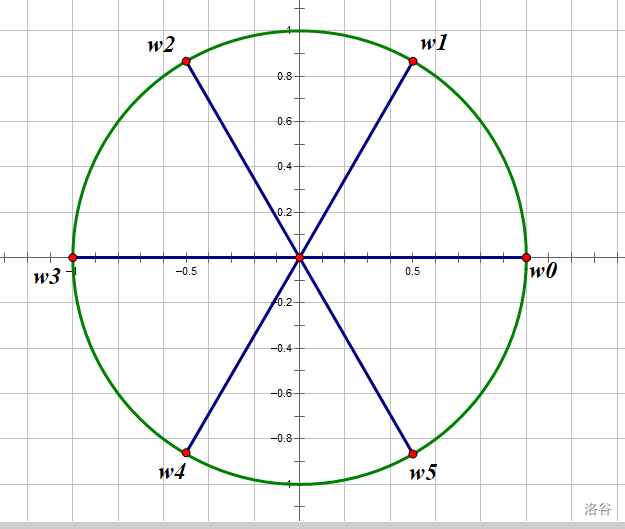
类似的，\(n\) 次单位根记为 \(\omega_n^0\) ，\(\omega_n^1\)，\(\omega_n^2\)....\(\omega_n^{n-1}\)（逆时针标号）
2.性质
1.\(\omega_n^0=1\)
2.\(\omega_n^k=(\omega_n^1)^k\)
3.\(\omega_n^i \times \omega_n^j=\omega_n^{i+j}\)
4.\(\omega_n^k=\omega_n^{k\%n}\)
5.\(\omega_{pn}^{pk}=\omega_n^k\)
6.\(\omega_n^{k+\frac{n}{2}}=-\omega_n^k\) (\(n\) 为偶数)
7.\(\omega_n^k=(\cos \frac{2k\pi}{n},\sin \frac{2k\pi}{n})\)
8.\(\sum_{i=0}^{n-1}\omega_n^i=0\)
\[\sum_{i=0}^{n-1}\omega_n^i=\frac{\omega_n^0(1-\omega_n^{n-1})}{1-\omega_n^1}=0
\]
三.多项式的表示
系数表示法
一个 \(n-1\) 次多项式一共有 \(n\) 项，每项前面的数字称为系数。
\[f(x)=f_0+f_1x+f_2x^2+...+f_{n-1}x^{n-1}
\]
是最常见的一种表示方法，但乘法需要 \(\Theta(n^2)\)。
点值表示法
还记得周考卷的已知两点求直线解析式吗？
其实直线可以看做一个 \(1\) 次多项式，我们知道两点即可得到解析式。
那么对于 \(n\) 次多项式，只需要知道 \(n+1\) 个取值即可唯一确定。
两个点值表示多项式的乘法只需要 \(\Theta(n)\)。
fft理论
既然点值表示法的乘法复杂度低，那么我们就可以将两个多项式由系数表示转化为点值表示，相乘后再还原为系数表示。
将多项式由系数表示到点值表示叫做离散傅里叶变换（\(\text{dft}\)），由点值表示到系数表示叫做逆离散傅里叶变换（\(\text{idft}\)）。
四.（逆）离散傅里叶变换（DFT/IDFT）
以下的 \(n\) 均为 \(2\) 的幂。
1.离散傅里叶变换
考虑一个 \(n\) 项多项式 \(f(x)\)。
\[f(x)=f_0+f_1x+f_2x^2+...+f_{n-1}x^{n-1}
\]
按奇偶分成两部分：
\[f(x)=(f_0+f_2x^2....+f_{n-2}x^{n-2})+(f_1+f_3x^3+...+f_{n-1}x^{n-1})
\]
又有两个 \(n/2\) 项多项式 \(fl,fr\)。
\[fl(x)=f_0+f_2x+...+f_{n-2}x^{n/2-1}
\]
\[fl(x)=f_1+f_3x+...+f_{n-1}x^{n/2-1}
\]
那么有: \(f(x)=fl(x^2)+xfr(x^2)\)
对于 \(k(k < \frac{n}{2})\) 分别代入 \(\omega_n^k\) ， \(\omega_n^{k+n/2}\) 得到。
\[\begin{aligned}
f(\omega_n^k)&=fl((\omega_n^k)^2)+\omega_n^kfr((\omega_n^k)^2) \\
&=fl(\omega_{n/2}^k)+\omega_n^kfr(\omega_{n/2}^k)
\end{aligned}\]
\[\begin{aligned}
f(\omega_n^{k+n/2})&=fl((\omega_n^{k+n/2})^2)+\omega_n^{k+n/2}fr((\omega_n^{k+n/2})^2) \\
&=fl((\omega_n^{k+n/2})^2)-\omega_n^kfr((\omega_n^{k+n/2})^2) \\
&=fl(\omega_n^{2k+n})-\omega_n^k fr(\omega_n^{2k+n}) \\
&=fl(\omega_n^{2k})-\omega_n^k fr(\omega_n^{2k}) \\
&=fl(\omega_{n/2}^k)-\omega_n^k fr(\omega_{n/2}^k) \\
\end{aligned}\]
然后我们会惊奇的发现，两个式子只有一个符号的区别。
现在就可以进行分治了。
2.逆离散傅里叶变换
不妨记 \(D_k\) 为多项式 \(f\) 在 \(\omega_n^k\) 的点值表示 ,则有
\[nf_k=\sum_{i=0}^{n-1}(\omega_n^{-k})^i D_i
\]
证明：
根据点值的意义可得：
\[D_k=\sum_{i=0}^{n-1}f_i(\omega_n^k)^i
\]
那么代入 \(D_i\)
\[\begin{aligned}
nf_i&=\sum_{i=0}^{n-1} (\omega_n^{-k})^i D_i \\
&= \sum_{i=0}^{n-1} (\omega_n^{-k})^i \sum_{j=0}^{n-1}(\omega_n^i)^j f_j \\
&=\sum_{i=0}^{n-1} \sum_{j=0}^{n-1} (\omega_n^{i})^{j-k} f_j \\
&=\sum_{j=0}^{n-1} f_j \sum_{i=0}^{n-1} (\omega_n^{j-k})^i \\
\end{aligned}\]
可以看出：
-
当 \(j=k\) 时，后一个和式的值为 \(n\)
-
当 \(j \not= k\) 时，由等比数列得：
\[\begin{aligned}
&=\sum_{j=0}^{n-1} f_j \sum_{i=0}^{n-1} \frac{1-\omega_n^{(j-k)n}}{1-\omega_n^{j-k}} \\
&=\sum_{j=0}^{n-1} f_j \sum_{i=0}^{n-1} \frac{1-1}{1-\omega_n^{j-k}} \\
&= 0
\end{aligned}\]
所以原式为: \(nf_k\)
3.实现
void fft( Complex *F , int len , int op ) {
if( len == 1 ) return;
Complex *Fl = F , *Fr = F + len / 2;
for( int i = 0 ; i < len ; i ++ ) tmp[ i ] = F[ i ];
for( int i = 0 ; i < len / 2 ; i ++ )
Fl[ i ] = tmp[ i << 1 ] , Fr[ i ] = tmp[ i << 1 | 1 ];
fft( Fl , len / 2 , op );
fft( Fr , len / 2 , op );
Complex w = { cos( 2 * pi / len ) , op * sin( 2 * pi / len ) } , buf = { 1 , 0 };
for( int i = 0 ; i < len / 2 ; i ++ ) {
tmp[ i ] = Fl[ i ] + buf * Fr[ i ]; //*
tmp[ i + len / 2 ] = Fl[ i ] - buf * Fr[ i ];
buf = buf * w;
}
for( int i = 0 ; i < len ; i ++ ) F[ i ] = tmp[ i ];
}
很显然，递归版本因为常数太大 \(T\) 掉了，考虑优化常数。
注意到 \((*)\) 处的 \(buf*Fr[i]\) 计算了两次，但复数乘法极慢，可以用变量存下来。
但还是过不了，我们需要一种常数更小的写法。
五.快速傅里叶变换
看一下离散傅里叶变换中的下标变化：
\[0,1,2,3,4,5,6,7
\]
\[0,2,4,6,1,3,5,7
\]
\[0,4,2,6,1,5,3,7
\]
把它们的二进制写出来，即
\[\begin{cases}
0(000) \rightarrow 0(000) \\
1(001) \rightarrow 4(100) \\
2(010) \rightarrow 2(010) \\
3(011) \rightarrow 6(110) \\
4(100) \rightarrow 1(001) \\
5(101) \rightarrow 5(101) \\
6(110) \rightarrow 3(011) \\
7(111) \rightarrow 7(111)
\end{cases}\]
经过观察发现，原数列位置的二进制反转后得到现在的位置。我不会证
然后就可以迭代实现了。
六.拆系数 fft (mtt)
7 次版本
正常的 fft 最大系数为 \(np^2\) ，会掉精度，所以考虑减小系数。
不妨设一个阈值 \(base\) , 将 \(f,g\) 划分为两部分。
令 \([x^n]A_0=\lfloor \frac{[x^n]f(x)}{base} \rfloor,[x^n]A_1(x)=[x^n]f(x) \bmod base\)。同理得 \(B_0,B_1\)。
可以看出，当 \(base\) 取 \(\sqrt p\) 附近时，多项式的最大系数为 \(np\)。
那么有:
\[\begin{cases}
f(x)=baseA_0(x)+A_1(x) \\
g(x)=baseB_0(x)+B_1(x)
\end{cases}\]
\[\begin{aligned}
f(x) \times g(x) &= (baseA_0(x)+A_1(x))\times(baseB_0(x)+B_1(x)) \\
&= base^2A_0(x)B_0(x)+base(A_0(x)B_1(x)+A_1(x)B_0(x)) + A_1(x)B_1(x)
\end{aligned}\]
那么可以 4 次 dft + 3 次 idft 计算。
可能有人(比如我)会问为什么不把点值加起来最后一次 idft 回去，但这样值域又会变很大，idft 时精度会炸。
#include <cmath>
#include <cstdio>
#include <vector>
#include <iostream>
using namespace std;
#define pi acos( -1 )
#define double long double
int Mod;
int Add( int x , int y ) { x += y; return x >= Mod ? x - Mod : x; }
int Sub( int x , int y ) { x -= y; return x < 0 ? x + Mod : x; }
struct Complex {
double x , y;
Complex(){ x = y = 0; }
Complex( double X , double Y ) { x = X , y = Y; }
Complex operator + ( const Complex &a ) const { return Complex( x + a.x , y + a.y ); }
Complex operator - ( const Complex &a ) const { return Complex( x - a.x , y - a.y ); }
Complex operator * ( const Complex &a ) const { return Complex( x * a.x - y * a.y , x * a.y + y * a.x ); }
Complex operator / ( const double &a ) const { return Complex( x / a , y / a ); }
};
#define Poly vector< Complex >
#define Polyint vector< int >
#define len( x ) ( (int)x.size() )
const int MAXN = 4e6;
int lim , rev[ MAXN + 5 ];
void fft( Poly &f , int op ) {
for( int i = 0 ; i < lim ; i ++ ) if( i < rev[ i ] ) swap( f[ i ] , f[ rev[ i ] ] );
for( int len = 2 ; len <= lim ; len <<= 1 ) {
Complex w( cos( (double)2 * pi / len ) , op * sin( (double)2 * pi / len ) );
for( int l = 0 ; l < lim ; l += len ) {
Complex wk( 1 , 0 );
for( int i = l ; i < l + len / 2 ; i ++ , wk = wk * w ) {
Complex t = wk * f[ i + len / 2 ];
f[ i + len / 2 ] = f[ i ] - t; f[ i ] = f[ i ] + t;
}
}
}
if( op == -1 ) for( int i = 0 ; i < lim ; i ++ ) f[ i ] = f[ i ] / lim;
}
Poly A0 , A1 , B0 , B1;
Polyint mtt( Polyint f , Polyint g , int Mod ) {
int n = len( f ) + len( g ) - 1; for( lim = 1 ; lim < n ; lim <<= 1 );
for( int i = 0 ; i < lim ; i ++ ) rev[ i ] = ( rev[ i >> 1 ] >> 1 ) | ( i & 1 ? lim >> 1 : 0 );
int base = 1 , lg = 0; for( ; 1ll * base * base < Mod ; base <<= 1 , lg ++ );
A0.resize( lim ); A1.resize( lim );
B0.resize( lim ); B1.resize( lim );
for( int i = 0 ; i < len( f ) ; i ++ ) A0[ i ].x = f[ i ] / base , A1[ i ].x = f[ i ] % base;
for( int i = 0 ; i < len( g ) ; i ++ ) B0[ i ].x = g[ i ] / base , B1[ i ].x = g[ i ] % base;
fft( A0 , 1 ); fft( A1 , 1 ); fft( B0 , 1 ); fft( B1 , 1 );
Poly tmp; tmp.resize( lim );
Polyint h; h.resize( lim );
for( int i = 0 ; i < lim ; i ++ ) tmp[ i ] = A0[ i ] * B0[ i ];
fft( tmp , -1 );
for( int i = 0 ; i < lim ; i ++ ) h[ i ] = Add( h[ i ] , (long long)( tmp[ i ].x + 0.49 ) % Mod * base * base % Mod % Mod );
for( int i = 0 ; i < lim ; i ++ ) tmp[ i ] = A0[ i ] * B1[ i ] + A1[ i ] * B0[ i ];
fft( tmp , -1 );
for( int i = 0 ; i < lim ; i ++ ) h[ i ] = Add( h[ i ] , (long long)( tmp[ i ].x + 0.49 ) % Mod * base % Mod );
for( int i = 0 ; i < lim ; i ++ ) tmp[ i ] = A1[ i ] * B1[ i ];
fft( tmp , -1 );
for( int i = 0 ; i < lim ; i ++ ) h[ i ] = Add( h[ i ] , (long long)( tmp[ i ].x + 0.49 ) % Mod );
h.resize( n );
return h;
}
int n , m;
Polyint f , g; Polyint h;
int main( ) {
scanf("%d %d %d",&n,&m,&Mod);
f.resize( n + 1 ); g.resize( m + 1 );
for( int i = 0 , x ; i <= n ; i ++ ) scanf("%d",&x) , f[ i ] = x % Mod;
for( int i = 0 , x ; i <= m ; i ++ ) scanf("%d",&x) , g[ i ] = x % Mod;
h = mtt( f , g , Mod );
for( int i = 0 ; i < len( h ) ; i ++ ) printf("%d ", h[ i ] );
return 0;
}
4 次版本
首先可以发现， \(dft\) 时虚部都为 \(0\)。
对于两个点值表达式, \(F(k)=A(\omega_n^k)+iB(\omega_n^k)\) , \(G(k)=A(\omega_n^k)-iB(\omega_n^k)\)
\[\begin{aligned}
F(k)&=\sum_{j=0}^{n-1} a_j \omega_n^{kj}+i\sum_{j=0}^{n-1}b_j\omega_n^{kj} \\
&= \sum_{j=0}^{n-1}(a_j+ib_j)\omega_n^{kj} \\
&= \sum_{j=0}^{n-1} (a_j+ib_j)\left( \cos (\frac{2\pi kj}{n}) + i \sin(\frac{2\pi kj}{n})\right) \\
\end{aligned}\]
同理有：
\[\begin{aligned}
G(n-k)&= A(\omega_n^{-k})+B(\omega_n^{-k})\\
&=\sum_{j=0}^{n-1} a_j \omega_n^{-kj}-i\sum_{j=0}^{n-1}b_j\omega_n^{-kj} \\
&= \sum_{j=0}^{n-1}(a_j-ib_j)\omega_n^{-kj} \\
&= \sum_{j=0}^{n-1} (a_j-ib_j)\left( \cos (\frac{2\pi kj}{n}) - i \sin(\frac{2\pi kj}{n})\right) \\
\end{aligned}\]
可以看出，\(F(k)\) 和 \(G(n-k)\) 是共轭复数。
并且，我们可以根据 \(F(k)\) 和 \(G(n-k)\) 求得 \(A(x)\) 和 \(B(x)\)。
那么将拆分出的 4 个多项式分别放到实部和虚部，可以用 2 次 dft 求得点值。
同理我们可以将两个点值序列分别放进点值的实部和虚部，idft 后实部和虚部的系数便为两个多项式的系数表示。
那么只需 2 次 idft 即可完成上述操作。
#include <cmath>
#include <cstdio>
#include <vector>
#include <iostream>
using namespace std;
#define pi acos( -1 )
#define double long double
int Mod;
int Add( int x , int y ) { x += y; return x >= Mod ? x - Mod : x; }
int Sub( int x , int y ) { x -= y; return x < 0 ? x + Mod : x; }
struct Complex {
double x , y;
Complex(){ x = y = 0; }
Complex( double X , double Y ) { x = X , y = Y; }
Complex operator + ( const Complex &a ) const { return Complex( x + a.x , y + a.y ); }
Complex operator - ( const Complex &a ) const { return Complex( x - a.x , y - a.y ); }
Complex operator * ( const Complex &a ) const { return Complex( x * a.x - y * a.y , x * a.y + y * a.x ); }
Complex operator / ( const double &a ) const { return Complex( x / a , y / a ); }
Complex operator * ( const double &a ) const { return Complex( x * a , y * a ); }
Complex Conj() { return Complex( x , -y ); }
};
#define Poly vector< Complex >
#define Polyint vector< int >
#define len( x ) ( (int)x.size() )
const int MAXN = 4e6;
int lim , rev[ MAXN + 5 ];
void fft( Poly &f , int op ) {
for( int i = 0 ; i < lim ; i ++ ) if( i < rev[ i ] ) swap( f[ i ] , f[ rev[ i ] ] );
for( int len = 2 ; len <= lim ; len <<= 1 ) {
Complex w( cos( (double)2 * pi / len ) , op * sin( (double)2 * pi / len ) );
for( int l = 0 ; l < lim ; l += len ) {
Complex wk( 1 , 0 );
for( int i = l ; i < l + len / 2 ; i ++ , wk = wk * w ) {
Complex t = wk * f[ i + len / 2 ];
f[ i + len / 2 ] = f[ i ] - t; f[ i ] = f[ i ] + t;
}
}
}
if( op == -1 ) for( int i = 0 ; i < lim ; i ++ ) f[ i ] = f[ i ] / lim;
}
void mtt( Poly f , Poly &A , Poly &B ) {
fft( f , 1 ); A.resize( lim ); B.resize( lim );
Poly g; g.resize( lim );
g[ 0 ] = f[ 0 ].Conj(); for( int i = 1 ; i < lim ; i ++ ) g[ lim - i ] = f[ i ].Conj();
for( int i = 0 ; i < lim ; i ++ ) {
A[ i ] = ( f[ i ] + g[ i ] ) * 0.5;
B[ i ] = ( f[ i ] - g[ i ] ) * 0.5 * Complex( 0 , -1 );
}
}
Poly F , G , A0 , A1 , B0 , B1;
Polyint mtt( Polyint f , Polyint g , int Mod ) {
int n = len( f ) + len( g ) - 1; for( lim = 1 ; lim < n ; lim <<= 1 );
for( int i = 0 ; i < lim ; i ++ ) rev[ i ] = ( rev[ i >> 1 ] >> 1 ) | ( i & 1 ? lim >> 1 : 0 );
int base = 1 , lg = 0; for( ; 1ll * base * base < Mod ; base <<= 1 , lg ++ );
F.resize( lim ); G.resize( lim );
for( int i = 0 ; i < len( f ) ; i ++ ) F[ i ].x = f[ i ] >> lg , F[ i ].y = f[ i ] & ( base - 1 );
for( int i = 0 ; i < len( g ) ; i ++ ) G[ i ].x = g[ i ] >> lg , G[ i ].y = g[ i ] & ( base - 1 );
mtt( F , A0 , A1 ); mtt( G , B0 , B1 );
Poly tmp1 , tmp2;
tmp1.resize( lim ); tmp2.resize( lim );
for( int i = 0 ; i < lim ; i ++ ) {
tmp1[ i ] = A0[ i ] * B0[ i ] + A1[ i ] * B1[ i ] * Complex( 0 , 1 );
tmp2[ i ] = A0[ i ] * B1[ i ] + A1[ i ] * B0[ i ] * Complex( 0 , 1 );
}
fft( tmp1 , -1 ); fft( tmp2 , -1 );
Polyint h; h.resize( lim );
for( int i = 0 ; i < lim ; i ++ ) {
h[ i ] = Add( h[ i ] , (long long)( tmp1[ i ].x + 0.49 ) % Mod * base * base % Mod % Mod );
h[ i ] = Add( h[ i ] , (long long)( tmp2[ i ].x + tmp2[ i ].y + 0.49 ) % Mod * base % Mod );
h[ i ] = Add( h[ i ] , (long long)( tmp1[ i ].y + 0.49 ) % Mod );
}
h.resize( n ); return h;
}
int n , m;
Polyint f , g; Polyint h;
int main( ) {
scanf("%d %d %d",&n,&m,&Mod);
f.resize( n + 1 ); g.resize( m + 1 );
for( int i = 0 , x ; i <= n ; i ++ ) scanf("%d",&x) , f[ i ] = x % Mod;
for( int i = 0 , x ; i <= m ; i ++ ) scanf("%d",&x) , g[ i ] = x % Mod;
h = mtt( f , g , Mod );
for( int i = 0 ; i < len( h ) ; i ++ ) printf("%d ", h[ i ] );
return 0;
}
