CF26D Tickets

不妨设 \(n+k>=m\) , 且 \(n < m\)。

回忆一下卡塔兰数的推导过程 ， 我们用类似的方法解决此题。

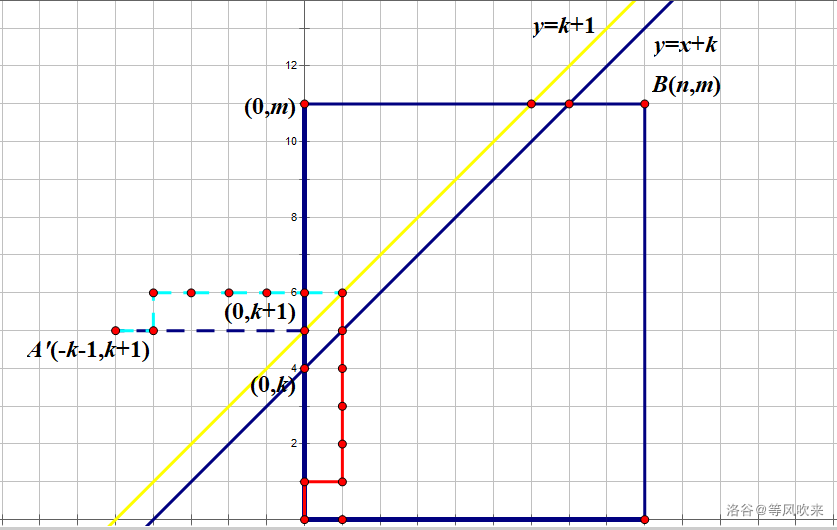
首先，我们可将题意转化成从 \((0,0)\) 到 \((n,m)\) ，不穿过 \(y=x+k\) 的一条路径。

将 \(y=x+k\) 向上平移一个单位得 \(y=x+k+1\) (黄色的函数)，原题等价于求一条路径且不经过 \(y=x+k+1\) 的路径。

从反面思考，我们只需找到经过 \(y=x+k+1\) 的路径即可。

我们不妨将 \(A(0,0)\) 关于 \(y=x+k+1\) 作对称得到 \(A'(-k-1,k+1)\)，发现对于每一条 \(A' \to B\) 的路径，都会穿过 \(y=x+k+1\) , 且一定有一条 \(A \to B\) 的路径与之对应。(蓝色虚线与红色实线)

那么经过 \(y=x+k+1\) 的路径的数量为 \(C_{n+m}^{n+k+1}\)

又因为从起点到终点的路径一共有 \(C_{n+m}^{n}\)

所以答案为 \(1-\frac{C_{n+m}^{n+k+1}}{C_{n+m}^{n}}\)

还有两种特殊情况：

1.\(k>=m\) ， 此时直接输出\(1\)。

2.\(n+k<m\) , 此时直接输出\(0\)。

这道题的 \(n,m\) 都很大，建议用自然对数的形式存阶乘。

#include <cstdio>
#include <cmath>

const int MAXN = 300000; 
int n , m , k;
double Ans , Fac[ MAXN + 5 ];

void Init( ) {
	Fac[ 0 ] = 0;
	for( int i = 1 ; i <= MAXN ; i ++ )
		Fac[ i ] = Fac[ i - 1 ] + log( i * 1.0 );
}
double C( int n , int m ) {
	return Fac[ n ] - Fac[ m ] - Fac[ n - m ];
}

int main( ) {
	Init( );
	scanf("%d %d %d",&n,&m,&k);
	if( k >= m ) 
		Ans = 1;
	else if( n + k < m ) 
		Ans = 0;
	else
		Ans = 1 - exp( C( n + m , n + k + 1 ) - C( n + m , n ) );
	printf("%.6lf",Ans);
	return 0;
}