【模式识别与机器学习】——3.1线性判别函数

3.1线性判别函数

3.1.1两类问题的判别函数

（1）以二维模式样本为例

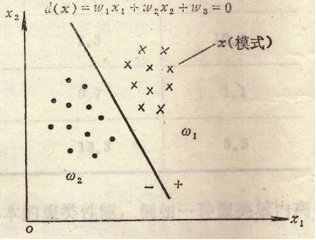
（2）用判别函数进行模式分类依赖的两个因素

① 判别函数的几何性质：线性的和非线性的函数。 线性的是一条直线； 非线性的可以是曲线、折线等； 线性判别函数建立起来比较简单（实际应用较多）； 非线性判别函数建立起来比较复杂。

② 判别函数的系数：判别函数的形式确定后，主要就是确定判别函数的系数问题。 只要被研究的模式是可分的，就能用给定的模式样本集来确定判别函数的系数。

3.1.2  n维线性判别函数的一般形式

（1）一个n维线性判别函数的一般形式：

 

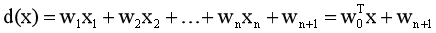
（2）两类情况：判别函数d(x)

 

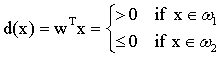
（3）多类情况：

设模式可分成ω1, ω2,…, ωM共M类，则有三种划分方法

① 多类情况1:

问题描述：用线性判别函数将属于ω_i类的模式与不属于ω_i类的模式分开，

其判别函数为：

        i = 1, 2, …, M

这种情况称为两分法，即把M类多类问题分成M个两类问题，因此共有M个判别函数，对应的判别函数的权向量为w_i, i = 1, 2, …, M。

图例：对一个三类情况，每一类模式可用一个简单的直线判别界面将它与其它类模式分开。例如，对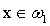的模式，应同时满足：d₁(x)>0，d₂(x)<0，d₃(x)<0

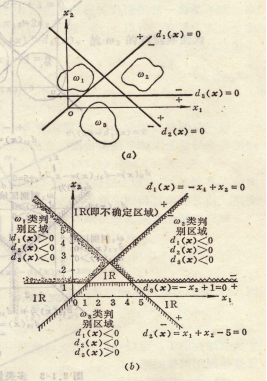
不确定区域：若对某一模式区域，d_i(x)>0的条件超过一个，或全部d_i(x)<0，i = 1, 2, …, M，则分类失败，这种区域称为不确定区域(IR)。

示例1：设有一个三类问题，其判别式为：

　　　　d₁(x)= -x₁ + x₂，d₂(x)= x₁ + x₂ - 5，d₃(x)= -x₂ + 1

则对一个模式x=(6, 5)^T，判断其属于哪一类。将x=(6, 5)^T代入上述判别函数，得：

　　　　d₁(x) = -1，故d₁(x)<0

　　　　d₂(x) = 6，故d₂(x)>0

　　　　d₃(x) = -4，故d₃(x)<0

从而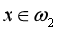

示例2：假若x=(3, 5)^T，则

　　　　d₁(x) = 2>0

　　　　d₂(x) = 3>0

　　　　d₃(x) = -2<0

分类失败。

② 多类情况2

问题描述：采用每对划分，即ω_i/ω_j两分法，此时一个判别界面只能分开两种类别，但不能把它与其余所有的界面分开。

其判别函数为：

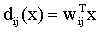　　　　　　    若d_ij(x)>0，，则重要性质：d_ij = -d_ji

图例：对一个三类情况，d₁₂(x)=0仅能分开ω₁和ω₂类，不能分开ω₁和ω₃类。

若要分开M类模式，共需M(M-1)/2个判别函数。

不确定区域：若所有d_ij(x)，找不到，d_ij(x)>0的情况。

示例 1：设有一个三类问题，其判别函数为：

　　　　d₁₂(x)= -x₁ - x₂ + 5，d₁₃(x)= -x₁ + 3，d₂₃(x)= -x₁ + x₂

若x=(4, 3)^T，则：d₁₂(x) = -2，d₁₃(x) = -1，d₂₃(x) = -1

有：

　　　

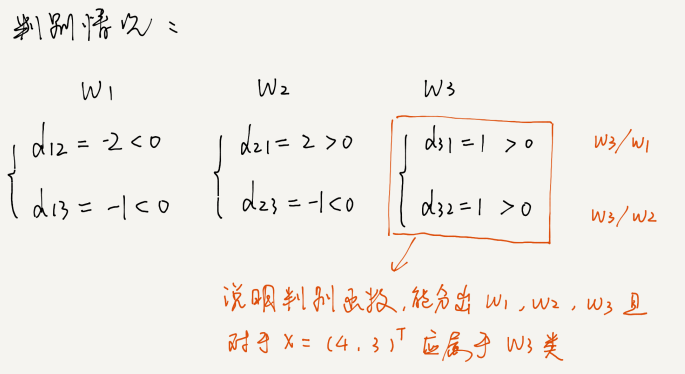
从而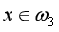

示例2：若x=(2.8, 2.5)^T，则：d₁₂(x) = -0.3，d₁₃(x) = 0.2，d₂₃(x) = -0.3

有：

　　　　

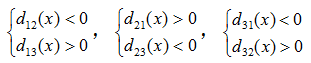
分类失败。

 

③ 多类情况3

这是没有不确定区域的ω_i/ω_j两分法。假若多类情况2中的d_ij可分解成：d_ij(x) = d_i(x) - d_j(x) = (w_i – w_j)^Tx，则d_ij(x)>0相当于d_i(x)>d_j(x)，这时不存在不确定区域。

此时，对M类情况应有M个判别函数：

　　　　　　

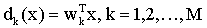
 即d_i(x)>d_j(x)，，i, j = 1,2,…,M则该分类的特点是把M类情况分成M-1个两类问题。

示例 1：设有一个三类问题的模式分类器，其判别函数为：

　　　　d₁(x)= -x₁ + x₂，d₂(x)= x₁ + x₂ - 1，d₃(x)= -x₂

属于ω₁类的区域应满足d₁(x)>d₂(x)且d₁(x)>d₃(x)，ω₁类的判别界面为：

　　　　d₁₂(x)= d₁(x)-d₂(x) = -2x₁ + 1 = 0

　　　　d₁₃(x)= d₁(x)-d₃(x) = -x₁ + 2x₂ = 0

属于ω₂类的区域应满足d₂(x)>d₁(x)且d₂(x)>d₃(x)，ω₂类的判别界面为：

　　　　d₂₁(x)= d₂(x)-d₁(x) = 2x₁ - 1 = 0，可看出d₂₁(x)=-d₁₂(x)

　　　　d₂₃(x)= d₂(x)-d₃(x) = x₁ + 2x₂ - 1= 0

属于ω₂类的区域应满足d₃(x)>d₁(x)且d₃(x)>d₂(x)，ω₃类的判别界面为：

　　　　d₃₁(x) = -d₁₃(x) = x₁ - 2x₂ = 0

　　　　d₃₂(x) = -d₂₃(x) = -x₁ - 2x₂ + 1= 0

【示例】

若有模式样本x=(1, 1)^T，则：d₁(x) = 0，d₂(x) = 1，d₃(x) = -1

从而：d₂(x)>d₁(x)且d₂(x)>d₃(x)，故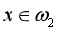

小结：

　　线性可分 模式分类若可用任一个线性函数来划分，则这些模式就称为线性可分的，否则就是非线性可分的。 一旦线性函数的系数wk被确定，这些函数就可用作模式分类的基础。

 

　　多类情况1和多类情况2的比较 对于M类模式的分类，多类情况1需要M个判别函数，而多类情况2需要M*(M-1)/2个判别函数，当M较大时，后者需要更多的判别式（这是多类情况2的一个缺点）。 采用多类情况1时，每一个判别函数都要把一种类别的模式与其余M-1种类别的模式分开，而不是将一种类别的模式仅与另一种类别的模式分开。 由于一种模式的分布要比M-1种模式的分布更为聚集，因此多类情况2对模式是线性可分的可能性比多类情况1更大一些（这是多类情况2的一个优点）。