Batch Normalization

 

前言：

Batch Normalization是深度学习领域在2015年非常热门的一个算法，许多网络应用该方法进行训练，并且取得了非常好的效果。

众所周知，深度学习是应用随机梯度下降法对网络进行训练，尽管随机梯度下降训练神经网络非常有效，但是它有一个缺点，就是需要人为的设定很多参数，比如学习率，权重衰减系数，Dropout比例等。这些参数的选择对训练结果至关重要，以至于训练的大多数精力都耗费在了调参上面。BN算法就可以完美的解决这些问题。当我们使用了BN算法，我们可以去选择比较大的初始学习率，这样就会加快学习的速度；我们还可以不必去理会过拟合中的dropout、正则项约束问题等，因为BN算法可以提高网络的泛化能力；我们再也不需要使用局部响应归一化层，因为BN本身就是归一化的网络；还可以打乱训练数据，防止每批训练的时候，某一个样本经常被选到。通常在训练神经网络之前，我们都会对数据进行归一化处理，为什么呢？因为神经网络训练实际是为了学习数据的分布情况，一旦训练数据与测试数据分布不同，那么网络的泛化能力也会大大降低。另外，如果每一批的训练数据都不同，那么神经网络就会去适应不同训练数据的分布，这样就会大大降低网络训练的速度。深度学习的训练是一个复杂的过程，如果前几层的数据分布发生了变化，那么后面就会积累下去，不断放大，这样就会导致神经网络在训练过程中不断适应新的数据分布，影响网络训练的速度。但是在网络训练的过程中，参数会不断的调整，除了输入层数据之外，后面网络每一层的输入分布在不断变化的（因为后面层的输入时前面层的输出，前面层的参数调整了，后面层的输入数据分布就会发生变化）。这样就会降低网络训练的速度。因此，BN算法就被提出。BN的算法本质是在网络每一层的输入前增加一层BN层（也即归一化层），对数据进行归一化处理，然后再进入网络下一层，但是BN并不是简单的对数据进行求归一化，而是引入了两个参数λ和β去进行数据重构(其中γ和β是可学习参数)

 

0 问题的发现

机器学习领域有个很重要的假设：IID独立同分布假设，就是假设训练数据和测试数据是满足相同分布的，这是通过训练数据获得的模型能够在测试集获得好的效果的一个基本保障。那BatchNorm的作用是什么呢？BatchNorm就是在深度神经网络训练过程中使得每一层神经网络的输入保持相同分布的。

covariate shift的概念：如果ML系统实例集合<X,Y>中的输入值X的分布老是变，这不符合IID假设，网络模型很难稳定的学规律，这不得引入迁移学习才能搞定吗，我们的ML系统还得去学习怎么迎合这种分布变化啊。对于深度学习这种包含很多隐层的网络结构，在训练过程中，因为各层参数不停在变化，所以每个隐层都会面临covariate shift的问题，也就是在训练过程中，隐层的输入分布老是变来变去，这就是所谓的“Internal Covariate Shift”，Internal指的是深层网络的隐层，是发生在网络内部的事情，而不是covariate shift问题只发生在输入层。

 

　　然后提出了BatchNorm的基本思想：能不能让每个隐层节点的激活输入分布固定下来呢？这样就避免了“Internal Covariate Shift”问题了。

 

　　BN不是凭空拍脑袋拍出来的好点子，它是有启发来源的：之前的研究表明如果在图像处理中对输入图像进行白化（Whiten）操作的话——所谓白化，就是对输入数据分布变换到0均值，单位方差的正态分布——那么神经网络会较快收敛，那么BN作者就开始推论了：图像是深度神经网络的输入层，做白化能加快收敛，那么其实对于深度网络来说，其中某个隐层的神经元是下一层的输入，意思是其实深度神经网络的每一个隐层都是输入层，不过是相对下一层来说而已，那么能不能对每个隐层都做白化呢？这就是启发BN产生的原初想法，而BN也确实就是这么做的，可以理解为对深层神经网络每个隐层神经元的激活值做简化版本的白化操作。

1 Batch Normalization（BN）的作用

1.1 特征分布对神经网络训练的作用

在神经网络的训练过程中，我们一般会将输入样本特征进行归一化处理，使数据变为均值为0，标准差为1的分布或者范围在0~1的分布。因为当我们没有将数据进行归一化的话，由于样本特征分布较散，可能会导致神经网络学习速度缓慢甚至难以学习。 
用2维特征的样本做例子。如下两个图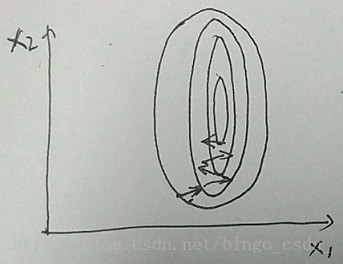 
 
上图中样本特征的分布为椭圆，当用梯度下降法进行优化学习时，其优化过程将会比较曲折，需要经过好久才能到达最优点。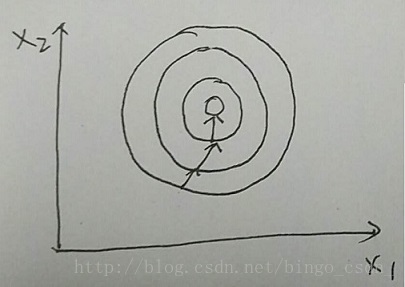 
 
上图中样本特征的分布为比较正的圆，当用梯度下降法进行优化学习时，其有过的梯度方向将往比较正确的方向走，训练比较快就到达最优点。 
因此一个比较好的特征分布将会使神经网络训练速度加快，甚至训练效果更好

1.2 BN的作用

但是我们以前在神经网络训练中，只是对输入层数据进行归一化处理，却没有在中间层进行归一化处理。要知道，虽然我们对输入数据进行了归一化处理，但是输入数据经过σ(WX+b)这样的矩阵乘法以及非线性运算之后，其数据分布很可能被改变，而随着深度网络的多层运算之后，数据分布的变化将越来越大。如果我们能在网络的中间也进行归一化处理，是否对网络的训练起到改进作用呢？答案是肯定的。 
这种在神经网络中间层也进行归一化处理，使训练效果更好的方法，就是批归一化Batch Normalization（BN）。BN在神经网络训练中会有以下一些作用：

（1）加快训练速度（2）可以省去dropout（3）L1, L2等正则化处理方法提高模型训练精度

2. BN的原理

既然BN这么厉害，那么BN究竟是怎么样的呢？ 
BN可以作为神经网络的一层，放在激活函数（如Relu）之前。BN的算法流程如下图： 

BN的基本思想其实相当直观：因为深层神经网络在做非线性变换前的激活输入值（就是那个x=WU+B，U是输入）随着网络深度加深或者在训练过程中，其分布逐渐发生偏移或者变动，之所以训练收敛慢，一般是整体分布逐渐往非线性函数的取值区间的上下限两端靠近（对于Sigmoid函数来说，意味着激活输入值WU+B是大的负值或正值），所以这导致反向传播时低层神经网络的梯度消失，这是训练深层神经网络收敛越来越慢的本质原因，而BN就是通过一定的规范化手段，把每层神经网络任意神经元这个输入值的分布强行拉回到均值为0方差为1的标准正态分布，其实就是把越来越偏的分布强制拉回比较标准的分布，这样使得激活输入值落在非线性函数对输入比较敏感的区域，这样输入的小变化就会导致损失函数较大的变化，意思是这样让梯度变大，避免梯度消失问题产生，而且梯度变大意味着学习收敛速度快，能大大加快训练速度。 THAT’S IT。其实一句话就是：对于每个隐层神经元，把逐渐向非线性函数映射后向取值区间极限饱和区靠拢的输入分布强制拉回到均值为0方差为1的比较标准的正态分布，使得非线性变换函数的输入值落入对输入比较敏感的区域，以此避免梯度消失问题。因为梯度一直都能保持比较大的状态，所以很明显对神经网络的参数调整效率比较高，就是变动大，就是说向损失函数最优值迈动的步子大，也就是说收敛地快。BN说到底就是这么个机制，方法很简单，道理很深刻。

上面说得还是显得抽象，下面更形象地表达下这种调整到底代表什么含义。

  图1  几个正态分布

　　假设某个隐层神经元原先的激活输入x取值符合正态分布，正态分布均值是-2，方差是0.5，对应上图中最左端的浅蓝色曲线，通过BN后转换为均值为0，方差是1的正态分布（对应上图中的深蓝色图形），意味着什么，意味着输入x的取值正态分布整体右移2（均值的变化），图形曲线更平缓了（方差增大的变化）。这个图的意思是，BN其实就是把每个隐层神经元的激活输入分布从偏离均值为0方差为1的正态分布通过平移均值压缩或者扩大曲线尖锐程度，调整为均值为0方差为1的正态分布。

　　那么把激活输入x调整到这个正态分布有什么用？首先我们看下均值为0，方差为1的标准正态分布代表什么含义：

 

图2  均值为0方差为1的标准正态分布图

 

　　这意味着在一个标准差范围内，也就是说64%的概率x其值落在[-1,1]的范围内，在两个标准差范围内，也就是说95%的概率x其值落在了[-2,2]的范围内。那么这又意味着什么？我们知道，激活值x=WU+B,U是真正的输入，x是某个神经元的激活值，假设非线性函数是sigmoid，那么看下sigmoid(x)其图形：

图3. Sigmoid(x)

及sigmoid(x)的导数为：G’=f(x)*(1-f(x))，因为f(x)=sigmoid(x)在0到1之间，所以G’在0到0.25之间，其对应的图如下：

图4  Sigmoid(x)导数图

　　假设没有经过BN调整前x的原先正态分布均值是-6，方差是1，那么意味着95%的值落在了[-8,-4]之间，那么对应的Sigmoid（x）函数的值明显接近于0，这是典型的梯度饱和区，在这个区域里梯度变化很慢，为什么是梯度饱和区？请看下sigmoid(x)如果取值接近0或者接近于1的时候对应导数函数取值，接近于0，意味着梯度变化很小甚至消失。而假设经过BN后，均值是0，方差是1，那么意味着95%的x值落在了[-2,2]区间内，很明显这一段是sigmoid(x)函数接近于线性变换的区域，意味着x的小变化会导致非线性函数值较大的变化，也即是梯度变化较大，对应导数函数图中明显大于0的区域，就是梯度非饱和区。

　　从上面几个图应该看出来BN在干什么了吧？其实就是把隐层神经元激活输入x=WU+B从变化不拘一格的正态分布通过BN操作拉回到了均值为0，方差为1的正态分布，即原始正态分布中心左移或者右移到以0为均值，拉伸或者缩减形态形成以1为方差的图形。什么意思？就是说经过BN后，目前大部分Activation的值落入非线性函数的线性区内，其对应的导数远离导数饱和区，这样来加速训练收敛过程。

　　但是很明显，看到这里，稍微了解神经网络的读者一般会提出一个疑问：如果都通过BN，那么不就跟把非线性函数替换成线性函数效果相同了？这意味着什么？我们知道，如果是多层的线性函数变换其实这个深层是没有意义的，因为多层线性网络跟一层线性网络是等价的。这意味着网络的表达能力下降了，这也意味着深度的意义就没有了。所以BN为了保证非线性的获得，对变换后的满足均值为0方差为1的x又进行了scale加上shift操作(y=scale*x+shift)，每个神经元增加了两个参数scale和shift参数，这两个参数是通过训练学习到的，意思是通过scale和shift把这个值从标准正态分布左移或者右移一点并长胖一点或者变瘦一点，每个实例挪动的程度不一样，这样等价于非线性函数的值从正中心周围的线性区往非线性区动了动。核心思想应该是想找到一个线性和非线性的较好平衡点，既能享受非线性的较强表达能力的好处，又避免太靠非线性区两头使得网络收敛速度太慢。