机器学习数学基础（线性代数）

Posted on 2018-08-15 15:01  Charlie_ODD  阅读(471)  评论(0)  编辑  收藏  举报

 2-1、标量

一个标量就是一个单独的数，一般用小写的的变量名称表示。

 2-2、向量

一个向量就是一列数，这些数是有序排列的。用过次序中的索引，我们可以确定每个单独的数。通常会赋予向量粗体的小写名称。当我们需要明确表示向量中的元素时，我们会将元素排列成一个方括号包围的纵柱：我们可以把向量看作空间中的点，每个元素是不同的坐标轴上的坐标。

2-3、矩阵

矩阵是二维数组，其中的每一个元素被两个索引而非一个所确定。我们通常会赋予矩阵粗体的大写变量名称，比如A。 如果一个实数矩阵高度为m，宽度为n，那么我们说A\epsilon R^{m\times n}。

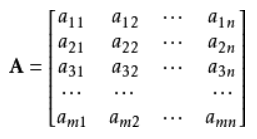
2-4、张量

几何代数中定义的张量是基于向量和矩阵的推广，通俗一点理解的话，我们可以将标量视为零阶张量，矢量视为一阶张量，那么矩阵就是二阶张量。例如，可以将任意一张彩色图片表示成一个三阶张量，三个维度分别是图片的高度、宽度和色彩数据。当然我们还可以将这一定义继续扩展，即：我们可以用四阶张量表示一个包含多张图片的数据集，这四个维度分别是：图片在数据集中的编号，图片高度、宽度，以及色彩数据。张量在深度学习中是一个很重要的概念，因为它是一个深度学习框架中的一个核心组件，后续的所有运算和优化算法几乎都是基于张量进行的。

2-5、范数

有时我们需要衡量一个向量的大小。在机器学习中，我们经常使用被称为范数(norm) 的函数衡量矩阵大小。Lp 范数如下：

\left| \left| x \right| \right| _{p}^{} =\left( \sum_{i}^{}{\left| x_{i} \right| ^{p} } \right) _{}^{\frac{1}{p} }

所以：

L1范数\left| \left| x \right| \right|：为x向量各个元素绝对值之和；

L2范数\left| \left| x \right| \right| _{2}：为x向量各个元素平方和的开方。

2-6、特征分解

许多数学对象可以通过将它们分解成多个组成部分。特征分解是使用最广的矩阵分解之一，即将矩阵分解成一组特征向量和特征值。

方阵A的特征向量是指与A相乘后相当于对该向量进行缩放的非零向量\nu：A\nu =\lambda \nu，标量\lambda被称为这个特征向量对应的特征值。 

使用特征分解去分析矩阵A时，得到特征向量构成的矩阵V和特征值构成的向量\lambda，我们可以重新将A写作：

A=Vdiag\left( \lambda \right) V^{-1}

2-7、奇异值分解（SVD）

除了特征分解，还有一种分解矩阵的方法，被称为奇异值分解（SVD）。将矩阵分解为奇异向量和奇异值。通过奇异分解，我们会得到一些类似于特征分解的信息。然而，奇异分解有更广泛的应用。每个实数矩阵都有一个奇异值分解，但不一定都有特征分解。例如，非方阵的矩阵没有特征分解，这时我们只能使用奇异值分解。奇异分解与特征分解类似，只不过这回我们将矩阵A分解成三个矩阵的乘积：

A=UDV^{T}

假设A是一个m\timesn矩阵，那么U是一个m\timesm矩阵，D是一个m\timesn矩阵，V是一个n\timesn矩阵。

这些矩阵每一个都拥有特殊的结构，其中U和V都是正交矩阵，D是对角矩阵（注意，D不一定是方阵）。对角矩阵D对角线上的元素被称为矩阵A的奇异值。矩阵U的列向量被称为左奇异向量，矩阵V 的列向量被称右奇异向量。

SVD最有用的一个性质可能是拓展矩阵求逆到非方矩阵上。另外，SVD可用于推荐系统中。

2-8、Moore-Penrose伪逆

对于非方矩阵而言，其逆矩阵没有定义。假设在下面问题中，我们想通过矩阵A的左逆B来求解线性方程：

Ax=y

等式两边同时左乘左逆B后，得到：

x=By

是否存在唯一的映射将A映射到B取决于问题的形式。

如果矩阵A的行数大于列数，那么上述方程可能没有解；如果矩阵A的行数小于列数，那么上述方程可能有多个解。

Moore-Penrose伪逆使我们能够解决这种情况，矩阵A的伪逆定义为：

 

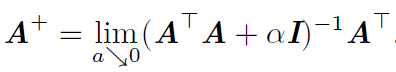但是计算伪逆的实际算法没有基于这个式子，而是使用下面的公式：

 

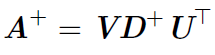其中，矩阵U，D 和V 是矩阵A奇异值分解后得到的矩阵。对角矩阵D 的伪逆D+ 是其非零元素取倒之后再转置得到的。

2-9、几种常用的距离

设有两个n维变量A=\left[ x_{11}, x_{12},...,x_{1n} \right]和B=\left[ x_{21} ,x_{22} ,...,x_{2n} \right]，则下面可以定义一些常用的距离公式：

1、曼哈顿距离

曼哈顿距离也称为城市街区距离，数学定义如下：

d_{12} =\sum_{k=1}^{n}{\left| x_{1k}-x_{2k} \right| }


曼哈顿距离的Python实现：

  1.  from numpy import *
  2.  vector1 = mat([1,2,3])
  3.  vector2 = mat([4,5,6])
  4.  print sum(abs(vector1-vector2))

2、欧氏距离

欧氏距离其实就是L2范数，数学定义如下： 

d_{12} =\sqrt{\sum_{k=1}^{n}{\left( x_{1k} -x_{2k} \right) ^{2} } }

欧氏距离的Python实现：

  1.  from numpy import *
  2.  vector1 = mat([1,2,3])
  3.  vector2 = mat([4,5,6])
  4.  print sqrt((vector1-vector2)*(vector1-vector2).T)

3、闵可夫斯基距离

从严格意义上讲，闵可夫斯基距离不是一种距离，而是一组距离的定义：

d_{12} =\sqrt[p]{\sum_{k=1}^{n}{\left( x_{1k} -x_{2k} \right) ^{p} } }

实际上，当p=1时，就是曼哈顿距离；当p=2时，就是欧式距离。

4、切比雪夫距离

切比雪夫距离就是L_{\varpi}，即无穷范数，数学表达式如下：

d_{12} =max\left( \left| x_{1k}-x_{2k} \right| \right)

切比雪夫距离额Python实现如下：

  1.  from numpy import *
  2.  vector1 = mat([1,2,3])
  3.  vector2 = mat([4,5,6])
  4.  print sqrt(abs(vector1-vector2).max)

5、夹角余弦

夹角余弦的取值范围为[-1,1]，可以用来衡量两个向量方向的差异；夹角余弦越大，表示两个向量的夹角越小；当两个向量的方向重合时，夹角余弦取最大值1；当两个向量的方向完全相反时，夹角余弦取最小值-1。

机器学习中用这一概念来衡量样本向量之间的差异，其数学表达式如下：

cos\theta =\frac{AB}{\left| A \right| \left|B \right| } =\frac{\sum_{k=1}^{n}{x_{1k}x_{2k} } }{\sqrt{\sum_{k=1}^{n}{x_{1k}^{2} } } \sqrt{\sum_{k=1}^{n}{x_{2k}^{2} } } }

夹角余弦的Python实现：

  1.  from numpy import *
  2.  vector1 = mat([1,2,3])
  3.  vector2 = mat([4,5,6])
  4.  print dot(vector1,vector2)/(linalg.norm(vector1)*linalg.norm(vector2))

6、汉明距离

汉明距离定义的是两个字符串中不相同位数的数目。

例如：字符串‘1111’与‘1001’之间的汉明距离为2。

信息编码中一般应使得编码间的汉明距离尽可能的小。

汉明距离的Python实现：

  1.  from numpy import *
  2.  matV = mat([1,1,1,1],[1,0,0,1])
  3.  smstr = nonzero(matV[0]-matV[1])
  4.  print smstr

7、杰卡德相似系数

两个集合A和B的交集元素在A和B的并集中所占的比例称为两个集合的杰卡德相似系数，用符号J(A,B)表示，数学表达式为：

J\left( A,B \right) =\frac{\left| A\cap B\right| }{\left|A\cup B \right| }

杰卡德相似系数是衡量两个集合的相似度的一种指标。一般可以将其用在衡量样本的相似度上。

8、杰卡德距离

与杰卡德相似系数相反的概念是杰卡德距离，其定义式为：

J_{\sigma} =1-J\left( A,B \right) =\frac{\left| A\cup B \right| -\left| A\cap B \right| }{\left| A\cup B \right| }

杰卡德距离的Python实现：

    1.  from numpy import *
    2.  import scipy.spatial.distance as dist
    3.  matV = mat([1,1,1,1],[1,0,0,1])
    4.  print dist.pdist(matV,'jaccard')