一、理解隐马尔科夫
1.1 举例理解
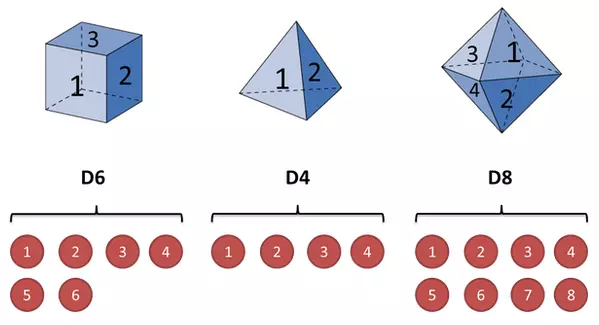
当我们无法观测到时使用哪个骰子投掷，仅仅能看到投掷的结果的时候。例如我们得到一个序列值：1 6 3 5 2 7 3 5 2 4。
它其实包含了：1、隐含的状态，选择了哪个骰子；2、可见状态，使用该骰子投出数值。如下：
而假设，每个状态间转移的概率（选择骰子的概率）是固定的（即为不因观测值的数值而改变）。可以得到状态转移矩阵。
那么我们得到观测值序列（1 6 3 5 2 7 3 5 2 4）出现概率的计算公式：
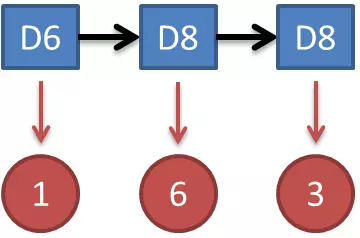
举前3个观测值（1 6 3）的例子，计算如下：
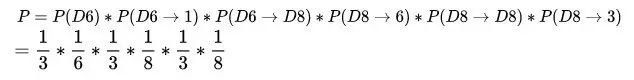
以上计算中，假设选择3个骰子的概率是相同的，都是1/3。
1.2 例子抽象
通过以上例子可以抽象一下，上面的例子中：
3种不同情况的骰子，即为：状态值集合（StatusSet）
所有可能出现的结果值（1、2、3、4、5、6、7、8）：观察值集合（ObservedSet）
选择不同骰子之间的概率：转移概率矩阵（TransProbMatrix ），状态间转移的概率
在拿到某个骰子，投出某个观测值的概率：发射概率矩阵（EmitProbMatrix ）-即：拿到D6这个骰子，投出6的概率是1/6。
最初一次的状态：初始状态概率分布（InitStatus ）
所以，很容易得到，计算概率的方法就是，初始状态概率分布（InitStatus ）、发射概率矩阵（EmitProbMatrix ）、转移概率矩阵（TransProbMatrix ）的乘积。
当某个状态序列的概率值最大，则该状态序列即为，出现该观测值的情况下，最可能出现的状态序列。
二、中文分词
HMM(Hidden Markov Model): 隐式马尔科夫模型。
HMM模型可以应用在很多领域，所以它的模型参数描述一般都比较抽象，以下篇幅针对HMM的模型参数介绍直接使用它在中文分词中的实际含义来讲：
2.1HMM的典型介绍就是这个模型是一个五元组:
StatusSet: 状态值集合
ObservedSet: 观察值集合
TransProbMatrix: 转移概率矩阵
EmitProbMatrix: 发射概率矩阵
InitStatus: 初始状态分布
2.2HMM模型可以用来解决三种问题：
（1）参数(StatusSet,TransProbMatrix,EmitRobMatrix,InitStatus)已知的情况下，求解观察值序列。(Forward-backward算法)
（2）参数(ObservedSet,TransProbMatrix,EmitRobMatrix,InitStatus)已知的情况下，求解状态值序列。(viterbi算法)
（3）参数(ObservedSet)已知的情况下，求解(TransProbMatrix,EmitRobMatrix,InitStatus)。(Baum-Welch算法)
其中，第三种问题最玄乎也最不常用，第二种问题最常用，【中文分词】，【语音识别】, 【新词发现】， 【词性标注】 都有它的一席之地。所以本文主要介绍第二种问题，即【viterbi算法求解状态值序列】的方法。
2.3五元组参数在中文分词中的具体含义
接下来我们讲实的，不讲虚的，针对中文分词应用，直接给五元组参数赋予具体含义：
（1）StatusSet & ObservedSet
状态值集合为(B, M, E, S): {B:begin, M:middle, E:end, S:single}。分别代表每个状态代表的是该字在词语中的位置，B代表该字是词语中的起始字，M代表是词语中的中间字，E代表是词语中的结束字，S则代表是单字成词。
观察值集合为就是所有汉字(东南西北你我他…)，甚至包括标点符号所组成的集合。状态值也就是我们要求的值，在HMM模型中文分词中，我们的输入是一个句子(也就是观察值序列)，输出是这个句子中每个字的状态值。比如:
小明硕士毕业于中国科学院计算所 输出的状态序列为 BEBEBMEBEBMEBES 根据这个状态序列我们可以进行切词: BE/BE/BME/BE/BME/BE/S 所以切词结果如下: 小明/硕士/毕业于/中国/科学院/计算/所
同时我们可以注意到：
B后面只可能接(M or E)，不可能接(B or S)。而M后面也只可能接(M or E)，不可能接(B, S)。
没错，就是这么简单，现在输入输出都明确了，下文讲讲输入和输出之间的具体过程，里面究竟发生了什么不可告人的秘密，请看下文：
上文只介绍了五元组中的两元【StatusSet, ObservedSet】，下文介绍剩下的三元【InitStatus, TransProbMatrix, EmitProbMatrix】。
这五元的关系是通过一个叫Viterbi的算法串接起来，ObservedSet序列值是Viterbi的输入，而StatusSet序列值是Viterbi的输出，输入和输出之间Viterbi算法还需要借助三个模型参数，分别是InitStatus, TransProbMatrix, EmitProbMatrix，接下来一一讲解：
（2）InitStatus
初始状态概率分布是最好理解的，可以示例如下：
B -0.26268660809250016 E -3.14e+100 M -3.14e+100 S -1.4652633398537678
示例数值是对概率值取对数之后的结果(可以让概率相乘的计算变成对数相加)，其中-3.14e+100作为负无穷，也就是对应的概率值是0。下同。也就是句子的第一个字属于{B,E,M,S}这四种状态的概率，如上可以看出，E和M的概率都是0，这和实际相符合，开头的第一个字只可能是词语的首字(B)，或者是单字成词(S)。
（3）TransProbMatrix
转移概率是马尔科夫链很重要的一个知识点，大学里面学过概率论的人都知道，马尔科夫链最大的特点就是当前T=i时刻的状态Status(i)，只和T=i时刻之前的n个状态有关。也就是:
{Status(i-1), Status(i-2), Status(i-3), … Status(i - n)}
更进一步的说，HMM模型有三个基本假设(具体哪三个请看文末备注)作为模型的前提，其中有个【有限历史性假设】，也就是马尔科夫链的n=1。即Status(i)只和Status(i-1)相关，这个假设能大大简化问题。回过头看TransProbMatrix，其实就是一个4x4(4就是状态值集合的大小)的二维矩阵，示例如下：
矩阵的横坐标和纵坐标顺序是BEMS x BEMS。(数值是概率求对数后的值，别忘了。)
1 -3.14e+100 -0.510825623765990 -0.916290731874155 -3.14e+100 2 -0.5897149736854513 -3.14e+100 -3.14e+100 -0.8085250474669937 3 -3.14e+100 -0.33344856811948514 -1.2603623820268226 -3.14e+100 4 -0.7211965654669841 -3.14e+100 -3.14e+100 -0.6658631448798212
比如TransProbMatrix[0][0]代表的含义就是从状态B转移到状态B的概率，由TransProbMatrix[0][0] = -3.14e+100可知，这个转移概率是0，这符合常理。由状态各自的含义可知，状态B的下一个状态只可能是ME，不可能是BS，所以不可能的转移对应的概率都是0，也就是对数值负无穷，在此记为-3.14e+100。
由上TransProbMatrix矩阵可知，对于各个状态可能转移的下一状态，且转移概率对应如下：
1 B 2 E:-0.510825623765990,M:-0.916290731874155 3 E 4 B:-0.5897149736854513,S:-0.8085250474669937 5 M 6 E:-0.33344856811948514,M:-1.2603623820268226 7 S 8 B:-0.7211965654669841,S:-0.6658631448798212
（4）EmitProbMatrix
这里的发射概率(EmitProb)其实也是一个条件概率而已，根据HMM模型三个基本假设(哪三个请看文末备注)里的【观察值独立性假设】，观察值只取决于当前状态值，也就是:
P(Observed[i], Status[j]) = P(Status[j]) * P(Observed[i]|Status[j])
其中P(Observed[i]|Status[j])这个值就是从EmitProbMatrix中获取。
EmitProbMatrix示例如下：
1 B 2 耀:-10.460283,涉:-8.766406,谈:-8.039065,伊:-7.682602,洞:-8.668696,… 3 E 4 耀:-9.266706,涉:-9.096474,谈:-8.435707,伊:-10.223786,洞:-8.366213,… 5 M 6 耀:-8.47651,涉:-10.560093,谈:-8.345223,伊:-8.021847,洞:-9.547990,…. 7 S 8 蘄:-10.005820,涉:-10.523076,唎:-15.269250,禑:-17.215160,洞:-8.369527…
虽然EmitProbMatrix也称为矩阵，这个矩阵太稀疏了，实际工程中一般是将上面四行发射转移概率存储为4个Map，详见代码HMMSegment。
到此，已经介绍完HMM模型的五元参数，假设现在手头上已经有这些参数的具体概率值，并且已经加载进来，(也就是有该模型的字典了，详见HMMDict里面的hmm_model.utf8)，那么我们只剩下Viterbi这个算法函数，这个模型就算可以开始使用了。所以接下来讲讲Viterbi算法。
2.4HMM中文分词之Viterbi算法
输入样例:
小明硕士毕业于中国科学院计算所
Viterbi算法计算过程如下：
定义变量
二维数组 weight[4][15]，4是状态数(0:B,1:E,2:M,3:S)，15是输入句子的字数。比如 weight[0][2] 代表 状态B的条件下，出现’硕’这个字的可能性。
二维数组 path[4][15]，4是状态数(0:B,1:E,2:M,3:S)，15是输入句子的字数。比如 path[0][2] 代表 weight[0][2]取到最大时，前一个字的状态，比如 path[0][2] = 1, 则代表 weight[0][2]取到最大时，前一个字(也就是明)的状态是E。记录前一个字的状态是为了使用viterbi算法计算完整个 weight[4][15] 之后，能对输入句子从右向左地回溯回来，找出对应的状态序列。
使用InitStatus对weight二维数组进行初始化
已知InitStatus如下:
1 B 2 -0.26268660809250016 3 E 4 -3.14e+100 5 M 6 -3.14e+100 7 S 8 -1.4652633398537678 9 且由EmitProbMatrix可以得出 10 11 Status(B) -> Observed(小) : -5.79545 12 Status(E) -> Observed(小) : -7.36797 13 Status(M) -> Observed(小) : -5.09518 14 Status(S) -> Observed(小) : -6.2475 15 所以可以初始化 weight[i][0] 的值如下： 16 17 weight[0][0] = -0.26268660809250016 + -5.79545 = -6.05814 18 weight[1][0] = -3.14e+100 + -7.36797 = -3.14e+100 19 weight[2][0] = -3.14e+100 + -5.09518 = -3.14e+100 20 weight[3][0] = -1.4652633398537678 + -6.2475 = -7.71276 21 注意上式计算的时候是相加而不是相乘，因为之前取过对数的原因。
遍历句子计算整个weight二维数组
1 //遍历句子，下标i从1开始是因为刚才初始化的时候已经对0初始化结束了 2 for(size_t i = 1; i < 15; i++) 3 { 4 // 遍历可能的状态 5 for(size_t j = 0; j < 4; j++) 6 { 7 weight[j][i] = MIN_DOUBLE; 8 path[j][i] = -1; 9 //遍历前一个字可能的状态 10 for(size_t k = 0; k < 4; k++) 11 { 12 double tmp = weight[k][i-1] + _transProb[k][j] + _emitProb[j][sentence[i]]; 13 if(tmp > weight[j][i]) // 找出最大的weight[j][i]值 14 { 15 weight[j][i] = tmp; 16 path[j][i] = k; 17 } 18 } 19 } 20 }
如此遍历下来，weight[4][15] 和 path[4][15] 就都计算完毕。
确定边界条件和路径回溯
边界条件如下：
对于每个句子，最后一个字的状态只可能是 E 或者 S，不可能是 M 或者 B。
所以在本文的例子中我们只需要比较 weight[1(E)][14] 和 weight[3(S)][14] 的大小即可。
在本例中：
weight[1][14] = -102.492; weight[3][14] = -101.632; 所以 S > E，也就是对于路径回溯的起点是 path[3][14]。 回溯的路径是: SEBEMBEBEMBEBEB 倒序一下就是: BE/BE/BME/BE/BME/BE/S 所以切词结果就是: 小明/硕士/毕业于/中国/科学院/计算/所
到此，一个HMM模型中文分词算法过程就阐述完毕了。
也就是给定我们一个模型，我们对模型进行载入完毕之后，只要运行一遍Viterbi算法，就可以找出每个字对应的状态，根据状态也就可以对句子进行分词。
模型的训练问题
以上讲的前提是基于模型来进行切词，也就是假设我们手头上的HMM模型已经是被训练好了的(也就是InitStatus, TransProbMatrix, EmitProbMatrix这三个模型的关键参数都是已知的)，没有涉及到这三个参数是如何得到的。这三个参数其实也是基于已分词完毕的语料进行统计计算，计算出相应的频率和条件概率就可以算出这三个参数。具体在此就不讲了。
备注
HMM模型的三个基本假设如下：
有限历史性假设:
P(Status[i]|Status[i-1],Status[i-2],… Status[1]) = P(Status[i]|Status[i-1]) 齐次性假设(状态和当前时刻无关): P(Status[i]|Status[i-1]) = P(Status[j]|Status[j-1]) 观察值独立性假设(观察值只取决于当前状态值): P(Observed[i]|Status[i],Status[i-1],…,Status[1]) = P(Observed[i]|Status[i])
https://www.jianshu.com/p/0eee07a5bf38
本文来自博客园，作者：Charlie_ODD，转载请注明原文链接：https://www.cnblogs.com/chihaoyuIsnotHere/p/10602852.html
